Внутренняя энергия газа. При условиях близких к нормальным (р = 100 кПа, Т = 273 К) молекулы газа можно считать практически не взаимодействующими между собой в том смысле

При условиях близких к нормальным (р = 100 кПа, Т = 273 К) молекулы газа можно считать практически не взаимодействующими между собой в том смысле, что потенциальной энергией их взаимодействия можно пренебречь. Другими словами, чтобы молекулам газа, содержащимся в некотором сосуде, разлететься в разные стороны на неограниченное расстояние друг от друга не требуется тратить энергию.

Это значит, что полная энергия газа равна сумме кинетических энергий составляющих его молекул

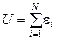, (10.2)

где e_i – кинетическая энергия i-й молекулы; N – число молекул.

Теоретически доказано, что средняя кинетическая энергия одной молекулы любого одноатомного газа равна

,

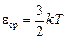где 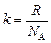= 1,38×10^–23 Дж/К – постоянная Больцмана. (Почему это так, мы выясним позже.)

Задача 10.1. Чему равна внутренняя энергия n молей одноатомного газа?

Решение. U = N×e_ср, где N – число молекул, а e_ср­ – средняя кинетическая энергия одной молекулы.

N = nN_A; .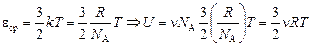

Ответ: внутренняя энергия n молей одноатомного газа, находящегося при температуре Т, равна

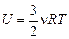. (10.3)

Для большинства двухатомных газов в условиях, близких к нормальным, можно считать среднюю кинетическую энергию молекулы равной

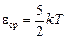. (10.4)

Рассуждая аналогично задаче 10.1, можно получить, что внутренняя энергия двухатомного газа в условиях, близких к нормальным, равна

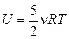. (10.5)

СТОП! Решите самостоятельно: В4.

Процесс, происходящий без теплообмена с внешней средой, называется адиабатическим.

Задача 10.2. Газ адиабатически расширяется. Как изменяется температура газа?

Решение. Согласно формуле (10.1) Q = (U₂ – U₁) + А. По определению адиабатического процесса Q = 0. Поскольку газ расширяется, то А > 0, следовательно, (U₂ – U₁) = –А < 0.

Ответ: U₂ < U₁, т.е. внутренняя энергия газа уменьшается, а значит, и температура газа уменьшается.

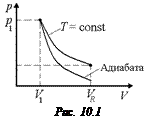Задача 10.3. Газ, имеющий в начальный момент параметры р₁, V₁, расширяется: 1) изотермически; 2) адиабатически до объема V₂ > V₁. Построить графики этих процессов в координатах (р, V).

Решение. Так как при адиабатическом расширении температура уменьшается, адиабата должна пройти ниже изотермы (см. рис. 10.1).

Ответ: см. рис. 10.1.

СТОП! Решите самостоятельно: В2.

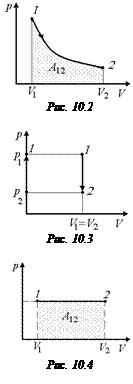
Задача 10.4. Газ изотермически расширяется. Получит ли при этом газ тепло от внешней среды или тепло отдаст?

Решение. Согласно формуле (10.1) Q₁₂ = A₁₂ + (U₂ – U­₁­). Если Q₁₂ > 0, значит, газ получит тепло, если Q₁₂< 0, то отдаст тепло.

Как видно из рис. 10.2, А₁₂ > 0. Так как процесс изотермический, то Т = const; следовательно, U = const; U₂ – U₁ = 0.

Значит,

Q_1-2 = A_1-2­ > 0.

Ответ: газ получит тепло от внешней среды.

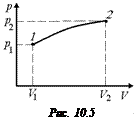
Задача 10.5. Газ изохорически охлаждается (V = const). Получит ли при этом газ тепло от внешней среды или отдаст?

Решение. Нарисуем график процесса в координатах (р, V) (рис. 10.3). Согласно формуле (10.1) Q_1-2 = A_1-2 + U₂ – U₁. Как видно из рисунка, А_1-2 = 0 (DV = 0).

Поскольку по условию задачи газ охлаждается, то Т₂ < Т₁, следовательно, U₂ < U₁, U₂ – U₁ < 0, отсюда Q_1-2 = U₂ – U₁ < 0.

Ответ: газ отдаст тепло.

Задача 10.6. Газ изобарически расширяется (р = const). Получит ли при этом газ тепло от внешней среды или отдаст?

Решение. Нарисуем график процесса в координатах (р, V) (рис. 10.4). Из графика видно, что А_1-2 > 0, Т₂ > Т₁, значит, U₂ > U₁. Следовательно,

Q_1-2 = А_1-2 + (U₂ – U₁) > 0.

Ответ: газ получит тепло от внешней среды.

Задача 10.7.Газ адиабатически сжимается. Получит ли при этом газ тепло от внешней среды или отдаст?

Решение. Адиабатический процесс проходит (по определению!) в теплоизолированной системе, т.е. газ не получает и не оттает тепла: Q = 0.

Ответ: Q = 0.

СТОП! Решите самостоятельно: А4, В3, В7, С7.

Задача 10.8. Одноатомный газ переходит из состояния с параметрами р₁, V₁ в состояние с параметрами р₂, V₂ по закону р = р(V) (рис. 10.5). Найти: 1) работу, совершенную газом; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

Решение.

1. 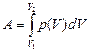(или площадь под графиком р(V) на участке [V₁V₂].

2. Согласно формуле (10.4)

DU = ,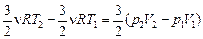

поскольку nRT₁ = p₁V₁, nRT₂ = p₂V₂.

3. .

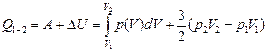Ответ: 1) 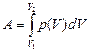; 2) DU = ;

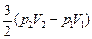3) .

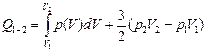Запомним формулу:

DU = 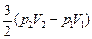. (10.6)

Задача 10.9. Одноатомный газ изохорически нагревается, переходя из состояния р₀, V₀ в состояние 2р₀, V₀. Найти: 1) работу, совершенную газом; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

		Решение. Построим график в координатах р, V (рис. 10.6). 1. А = 0, так как DV = 0. 2. Согласно формуле (10.6) DU = .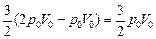
р0, 2р0 V0 V = const	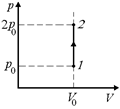Рис. 10.6
А = ? DU = ? Q = ?

3. Согласно формуле (10.1)

Q_1-2 = А_1-2 + DU = .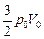

Ответ: 1) А = 0; 2) 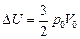; 3) Q_1-2 = .

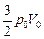Задача 10.10. Одноатомный газ изобарически расширяется от объема V₀ до объема 2V₀. Давление р₀ = const. Найти: 1) работу газа; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

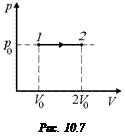
V1 = V0 V2 = 2V0 р0 = const	Решение. Построим график в координатах р, V (рис. 10.7). 1. Так как р0 = const, то А = р0DV = р0(2V0 – V0) = р0V0. 2. Согласно формуле (10.6) DU = .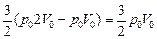
А = ? DU = ? Q = ?

3. Согласно формуле (10.1)

Q = А + DU = А + (U₂ – U₁) =

= p₀V₀ + = .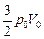

Ответ: 1) А = р₀V₀; 2) DU = ;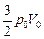

3) Q = .

Замечание. Точки (2р₀, V₀) и (р₀, 2V₀) соответствуют одной и той же температуре. В самом деле,

(2р₀)V₀ = р₀(2V₀), т.е. р₁V₁ = p₂V₂,

отсюда Т = const, так как рV = nRT. Значит, в задачах 10.9 и 10.10 газ нагрелся на одну и ту же DТ! Но в первом случае, нагреваясь при постоянном объеме, газ получил только Q_V = 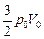тепла, а во втором случае, нагреваясь при постоянном давлении, газ получил Q_p = . То есть 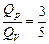(рис. 10.8). Следовательно, при изобарическом нагревании требуется больше тепла, чем при изохорическом на одну и ту же температуру!

СТОП! Решите самостоятельно: В5, В6, С1.

Задача 10.11. Одноатомный газ изотермически расширяется, переходя из состояния р₀, V₀ в состояние р₀/2, 2V₀. Найти: 1) работу, совершенную газом; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

р1 = р0 р2 = р0/2 V1 = V0 V2 = 2V0 T = const	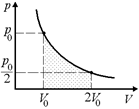Рис. 10.9	Решение. Построим график в координатах р, V (рис. 10.9). Поскольку Т2 = Т1, то и U2 = U1, значит, U2 – U1 = 0. Поскольку T = const, то по закону Бойля–Мариотта pV = p1V1, p = .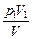
А = ? DU = ? Q = ?

Вычислим работу газа:

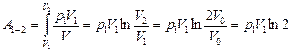= р₀V₀ln2.

Согласно формуле (10.1)

Q = А_1-2 + (U₂ – U₁) = р₀V₀ln2 + 0 = р₀V₀ln2.

Ответ: 1) А = р₀V₀ln2; 2) DU = 0; 3) Q = р₀V₀ln2.

СТОП! Решите самостоятельно: А6, С2.

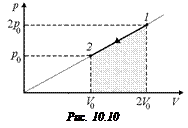Задача 10.12. Одноатомный газ сжимается по закону р = aV от состояния 2р₀, 2V₀ до состояния р₀, V_0­ (рис. 10.10). Найти: 1) работу, совершенную газом; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

р = aV р1 =2р0 р2 = р0 V1 = 2V0 V2 = V0	Решение. Работа, совершенная газом, равна площади под графиком р(V) на отрезке [V0; 2V0], взятой со знаком «минус»: 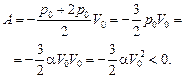Согласно формуле (10.6)
А = ? DU = ? Q = ?

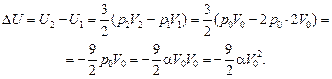
Согласно формуле (10.1)

,

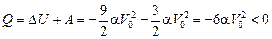т.е. газ отдает тепло.

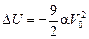Ответ: 1) ; 2) ; 3) .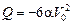

Задача 10.13. Одноатомный газ переходит из состояния 3р₀, V₀ в состояние р₀, 2V_0­ (рис. 10.11). Найти: 1) работу, совершенную газом; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом.

р1 =3р0 р2 = р0 V1 = V0 V2 = 2V0	Рис. 10.11 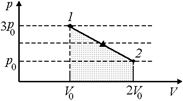  Решение. Работа, совершенная газом, равна площади под графиком р(V) на отрезке [V0; 2V0]:
А = ? DU = ? Q = ?

.

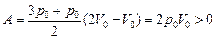Согласно формуле (10.6)

.

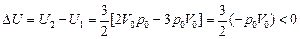Согласно формуле (10.1)

,

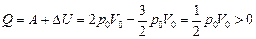т.е. газ получает тепло.

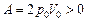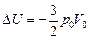Ответ: 1) ; 2) ; 3) .

СТОП! Решите самостоятельно: С4, С5.