Теплота химической реакции (при постоянном давлении или при постоянном объеме) не зависит от пути процесса, а определяется только начальным и конечным состояниями системы.
4. Проиллюстрируем данное утверждение на двух примерах.
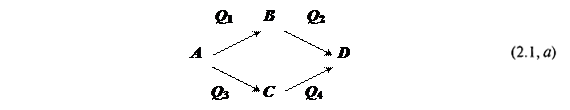 |
а) Во-первых, пусть имеются две параллельные цепи реакций:
Согласно закону,
Q1 + Q2 = Q3 + Q4 (2.1, б)
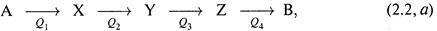 |
б) Во-вторых, пусть имеется цепь последовательных реакций:
Q0
при сопоставлении которой с непосредственным превращением А—›Ввновь получаем две параллельные цепи (где одна цепь представлена лишь одной реакцией). И, по аналогии с (2.1,6),можем записать:
 |
Вывод: теплота суммарного превращения равна сумме теплот нромежуточных стадий.
5. Что же касается работы, то нетрудно рассчитать работу реагирующей системы (или над ней), совершаемую против давления.
а) Так, пусть имеется реакция вида
 |
где вещество С — газ.
б) За счет образования газа объем системы увеличивается, и совершается работа против постоянного внешнего давления:
 |
 |
Под Vraз следует понимать такой объем, который образовавшийся газ занимает при собственном давлении, равном атмосферному. Отсюда
а это свидетельствует, что работа расширения определяется количеством образующегося газа.
в) Если в ходе реакции газ, наоборот, поглощается, работу совершает внешняя среда. Но формулы ее расчета остаются такими же.
г) Если же все участники реакции находятся в жидком или твердом состоянии, то работа против давления практически не совершается.
Энтальпия
Вернемся к теплоте реакций и других процессов.
1. Как было изложено выше, теплота процесса становится функцией состояния только при определенных условиях, однако в общем случае таковой не является.
 |
2. а) В связи с этим, в термодинамику введена другая величина — энтальпия:
Её определение сделано на основании формулы (1.10):
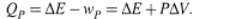 |
б) Особенность энтальпии состоит в том, что она всегда является функцией состояния.
Действительно, в определении (2.6) фигурируют только параметры Р, V и функция Е состояния.
Следовательно,во всех процессах ΔН (как и ΔЕ) зависит только от начального (1) и конечного (2) состояний:
 |
где H2 и H1 — энтальпии этих состояний.
 |
3. а) Тем не менее, для изобарного процесса изменение энтальпии равно теплоте:
б) Поэтому теплоту реакций можно находить по разности энтальпии продуктов и реагентов:
 |
вследствие чего теплоту обычно отождествляют с энтальпией.
в) Заметим: такое отождествление справедливо только при условии, что в ходе процесса не совершается никакой иной работы, кроме работы против давления.
г) Если же в изобарном процессе производится какая-то другая («полезная») работа, то теплота процесса отличается от ΔН на величину этой работы:
 |
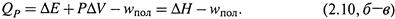 |
откуда
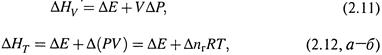 |
4. а) Для изохорногои изотермическогопроцессов изменение энтальпии таково:
где Δnг — изменение количества газообразных веществ.
б) Если все участники реакции — в жидком или твердом состоянии, то величинами ΔР иΔ (PV) можно пренебречь, и тогда
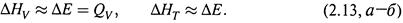 |
Как видно, для изохорного процесса изменение энтальпии вновь почти совпадает с теплотой.
5. Существует еще одно толкование энтальпии.
Поскольку PV — потенциальная энергия не только газообразных, но и жидких веществ, то Н = Е + PV — это сумма внутренней и потенциальной энергии системы.
Однако важней всего связь ΔН с теплотой.
2.3. Расчёт теплот реакций
Как же рассчитывать теплоты реакций, используя представление об энтальпии?
1. Поскольку в определение H входит Е, то абсолютное значение энтальпии системы (или какого-то вещества) неизвестно.
Поэтому энтальпию вещества характеризуют стандартными энтальпиями образования и сгорания.
а) ΔНообр (стандартная энтальпия образования) — это теплота реакции образования вещества из простых веществ (или элементов) при стандартных условиях:
простые вещества → X. (2.14, а)
При этом для самих простых веществ ΔНообр считается равной нулю.
б) А ΔНосг (стандартная энтальпия сгорания) — теплота реакции сгорания вещества до оксидов (с максимальной степенью окисления) при стандартных условиях:
Х + О2→ оксиды (с макс. СО). (2.14,б)
Здесь для указанных оксидов принимается, что ΔНосг = 0.
в) Величины ΔНосг определены для очень многих веществ экспериментальным способом — путем сжигания вещества в калориметрической «бомбе» и измерения выделяющейся теплоты.
Зная ΔНосг, можно вычислить и ΔНообр.
Эти значения (ΔНосг и ΔНообр) содержатся во многих справочных таблицах.
2. а) Для получения формул, показывающих, как пользоваться этими величинами, обратимся к простейшей реакции:
А → В (2.15)
ΔНрц
Здесь ΔНрц — теплота реакции.
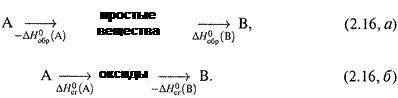 |
б) Теплота результирующего превращения не изменится (по закону Гесса), если его провести одним из двух таких способов:
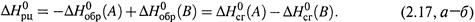 |
в) Отсюда получаем:
г) Обобщение этих выражений для произвольных реакций приводит к формулам:
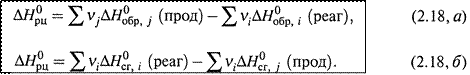 |
Здесь νi и νj — стехиометрические коэффициенты перед соответствующими веществами в уравнении реакции.
д) Таким образом, для расчета теплоты реакции по энтальпиям образованияследует из суммы энтальпий продуктов вычесть сумму энтальпий реагентов.
А при использовании энтальпий сгорания —наоборот, из суммы энтальпий реагентов вычесть сумму энтальпий продуктов.
3. Вот примеррасчета по этим формулам. Спиртовое брожение глюкозы у дрожжей:
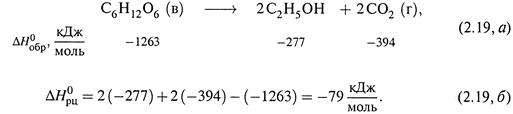 |
4. а) По знаку теплоты (т.е. ΔНорц) реакции подразделяются на
- экзотермические, где ΔНорц < 0 , т. е. теплота выделяется, и
- эндотермические, в которых ΔНорц > 0 — теплота поглощается.
б) Таким образом, приведенный выше процесс брожения глюкозы является экзотермическим.
2.4. Теплоёмкость веществ
Наряду с энтальпиями образования и сгорания непосредственное отношение к теплоте имеет теплоемкость.
1. Дадим определение: молярная теплоемкость вещества – это количество теплоты, требующееся для увеличения температуры 1 моля вещества на 1 градус:
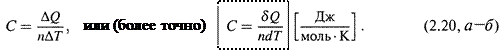 |
(Для обозначения бесконечно или малой теплоты в произвольном процессе здесь и далее используется знак δ, а не d, поскольку теплота может не являться функцией состояния, и тогда величина δQ зависит от способа осуществления данной микростадии процесса).
2. а) Известны два частных вида теплоемкости — CVиCP :
- в первом случае теплоемкость определяется при постоянном объеме,
- во втором — при постоянном давлении.
б) Учтем, что, согласно (1.11,б) и (2.9),
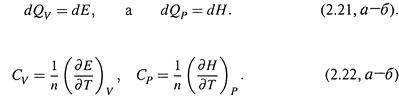
Отсюда
Как видим, CV — это производная внутренней энергии по температуре, отнесенная к 1 молю вещества, а CP— производная энтальпии.
3. Можно также установить связь этих двух величин между собой.
а) При P = const для идеальных газов
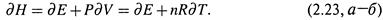 |
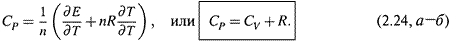 |
б) Подставляя последнее выражение в (2.22,б), получаем:
Таким образом, эти две теплоёмкости различаются всего на величину R ≈ 8,31 Дж/(моль∙К). Причём, это справедливо лишь для идеальных газов; в случае же жидких и твёрдых веществ СР = СV .
 |
4. а) Возвращаясь к идеальному газу, напомним:
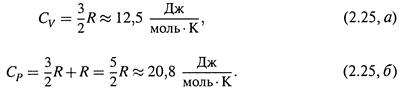 |
б) Поэтому для него, согласно (2.22, а) и (2.24,6),
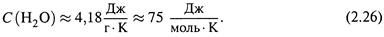 |
в) Для сравнения приведем теплоемкость воды в пределах 10°—20° С:
Как видно, она гораздо больше. Так что, в самом деле, оценки (2.25,а-б)справедливы только для идеального газа.
Дата добавления: 2016-03-20; просмотров: 941;
