Связь энтропии с теплотой обратимого процесса
Как конкретно определить изменение энтропии ΔS?
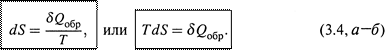 |
1. а) Расчеты основаны на следующем ключевом положении: изменение энтропии измеряется приведенной теплотой обратимого процесса, связывающего соответствующие состояния системы:
Заметим: речь идет о том, что энтропия именно измеряетсявеличиной δQобр/T, но вовсе не тождественна ей по смыслу.
б) Соотношения (3.4) основываются на следующих трех фактах.
I. Приведенная теплота обратимого микропроцесса δQобр/T, в отличие от просто теплоты δQ или даже теплоты обратимого микропроцесса δQобр, является функцией состоянияи не зависит от способа перехода из одного состояния в другое.
II. Функция, измеряемая данной величиной, в необратимых процессах в изолированных системах всегда возрастает, а значит, является критерием самопроизвольности процессов.
III. Одновременно эта функция непосредственно связана с числом микроостояний, возможных в системе, т. е. характеризует меру ее энергетического беспорядка.
в) Эти три факта соответствуют приведенным выше представлениям об энтропии — тому, что это функция состояния, причем, такая, которая является критерием самопроизвольных процессов в изолированных системах и отражает степень энергетического беспорядка системы. Отсюда и следует, что величиной δQобр/T измеряется изменение именно энтропии.
2. Но как убедиться в трёх перечисленных свойствах величины δQобр/T?
а) Доказательство второго и особенно третьего свойства достаточно сложно; эти утверждения читателю придётся принять на веру.
б) А вот первое утверждение (о том, что величина δQобр/T – функция состояния) мы рассмотрим более внимательно.
Его доказательство строится на том, что в циклическом процессе результирующее изменение любой функции состояния, очевидно, должно равняться нулю.
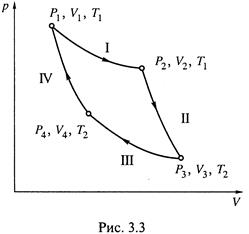
Поэтому обращаются к простейшей газовой системе и рассматривают в ней определённый циклический процесс – цикл Карно. Интеграл функции δQобр/T, действительно,оказывается равным нулю:
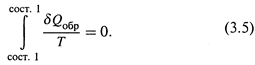
Убедимся в этом.
3. а)Цикл Карно(рис. 3.3) включает 4 обратимые стадии:
I) изотермическое расширениегаза от V1 до V2 при температуре T1; поглощается теплота Q1;
II) адиабатическое расширение газа от V2 до V3 (при этом Q = 0, а температура снижается от Т1 до Т2 );
III) изотермическое сжатиеот V3 до V4 при температуре Т2; отдается теплота Q2;
IV) адиабатическое сжатиеот V4 до V1; вновь Q = 0, а температура увеличивается до T1.
Напомним: адиабатическими называются такие процессы, в которых исключен теплообмен системы с окружающей средой (1.12).
б) Для изотермических стадий цикла воспользуемся формулами (1.8) и (1.6):
 |
в) А исходя из свойств адиабатических процессов, можно доказать, что
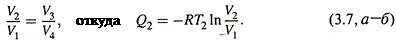 |
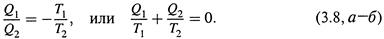 |
г) Учитывая это обстоятельство, поделим почленно соотношения (3.6,а-б) друг на друга:
д)Поскольку для адиабатических стадий Q = 0, получается, что результирующее изменение функции δQобр/T в цикле равно нулю. Что утверждалось соотношением (3.5) и откуда следует, что δQобр/T — функция состояния.
Дата добавления: 2016-03-20; просмотров: 1300;
