Дополнительные замечания
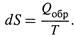 |
Итак, изменение энтропии измеряется приведенной теплотой обратимого процесса (3.4,а):
1. а) Следует обратить внимание на знаки в этом соотношении: если в указанном процессе теплота поглощается системой (δQобр > 0), то dS > 0— энергетический беспорядок в системе возрастает; если же система отдает теплоту (δQобр < 0), то dS < 0 — беспорядок уменьшается.
2. а) А температурный множитель показывает: если система обратимо получает (или отдает) теплоту при меньшей температуре, на энтропию это влияет сильней.
б) Действительно, пусть при T1 частицы системы имеют энергию по 200 Дж и в ходе процесса отдают в виде теплоты по 20 Дж. Их движения становятся более упорядоченными (dS < 0) всего лишь на 10 %.
Если же это происходит при такой низкой температуре T2, где частицы имеют по 40 Дж энергии, то потеря по 20 Дж скажется на энергетической упорядоченности гораздо сильней.
3.4. Расчет ΔS в некоторых процессах
а) На основании изложенного выше конкретные расчеты изменения энтропии в процессах проводятся по формуле:
 |
б) А для расчета абсолютного значения энтропии (S0, а не ΔS)используют третье начало термодинамики: при абсолютном нуле температуры энтропия любой системы равна нулю:

т.е. при данной температуре как бы достигается идеальный энергетический порядок. Это положение не доказывается, а принимается в качестве постулата, хотя опирается на определенные экспериментальные факты.
Рассмотрим вначале, как найти ΔS тех или иных процессах.
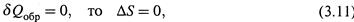 |
1. Обратимый адиабатический процесс. Поскольку на всех стадиях такого процесса
а значит, в обратимых адиабатических процессах энтропия системы не меняется.
2. Нагревание системы.
а) Нагревание при постоянном объеме или давлении — термодинамически обратимый процесс. Поэтому в формуле (3.9) в качестве δQобр (точнее, теперь уже dQобр) следует взять теплоту реального процесса, которую, в свою очередь, можно найти через теплоемкость.
б) Действительно, исходя из формул (2.20–2.22), для произвольного количества вещества имеем:
 |
Если полагать величину CP на рассматриваемом температурном интервале постоянной, то подстановка в (3.9) даёт:
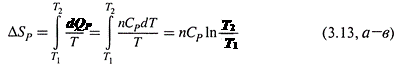 |
в) Аналогично, для нагревания воды при постоянном объёме
 |
г) Для жидких и твердых веществ CP = CV , поэтому для них
д) Из формул (3.13)—(3.14) видно, что
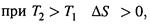 |
т. е. при нагревании степень энергетического беспорядка системы возрастает.
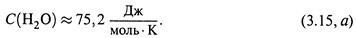 |
е) Пример. Теплоемкость воды —
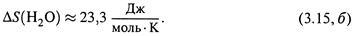 |
Используя ее, по формуле (3.13, в) находим изменение энтропии 1 моля воды при его нагревании от 0°С до 100°С, т.е. от T1= 273 Кдо Т 2 = 373 К:
3. Фазовые переходы.
а) Это тоже зачастую термодинамически обратимые процессы, которые при небольшом изменении условий могут сдвигаться в ту или иную сторону.
Для переходов в газ (ж↔г и тв↔г)это справедливо тогда, когда газ (пар) является насыщенным (что достигается обычно в закрытых сосудах). А для плавления (перехода тв↔ж) справедливо практически всегда.
б) Кроме того, в процессах типа ж↔г (при температуре кипения) и тв↔ж температура сохраняется постоянной; в процессах же типа тв↔ги ж↔г (при произвольной температуре) температуру поддерживают постоянной (для измерения теплоты перехода).
в) Поэтому в обоих случаях интегрирование не требуется.
Следовательно, ΔS опять-таки рассчитывается по теплоте процесса:
 |
 |
Пример 1. Теплота плавления льда такова:
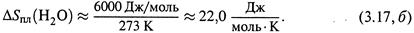 |
Учитывая, что Тпл = 273 К, находим:
Итак, плавление льда примерно так же увеличивает энтропию, как последующее нагревание воды на 100 градусов (3.15,б).
Пример 2. Аналогично можно найти изменение энтропии в результате испарения воды при температуре кипения (Ткип = 373 К).
Теплота испарения:
| Отсюда |
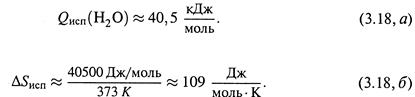
4. Абсолютная энтропия; энтропии образования и сгорания.
а) Как видно, часто достаточно оперировать изменениями энтропии, а не самими ее абсолютными значениями.
Тем не менее, исходя из третьего начала термодинамики (3.10), можно рассчитывать и абсолютную энтропию вещества или какой-то более сложной системы при некоей температуре Тх.
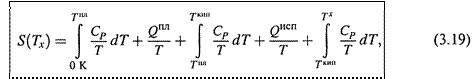 |
б) Пусть Тх выше температуры кипения. Тогда справедливо следующее выражение:
где учтены три этапа нагревания вещества и два фазовых перехода между ними.
В общем случае теплоёмкость, фигурирующая в (3.19), зависит от температуры. Поэтому её определяют в калориметре при разных температурах, строят график функции CP/T для каждого этапа и измеряют площадь под кривой (т.е. проводят интегрирование графическим способом).
в) В таблицах обычно приводят абсолютную энтропию (S0), относящуюся к стандартным условиям (1.3):
Т = 25° (298 К), Р=1 атм (101,3 кПа), п = 1 моль.
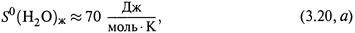 |
Например, для воды расчет по формуле (3.19) дает:
а для молекул пара воды при той же температуре, учитывая (3.18, б) и пренебрегая зависимостью ΔSисп от Т, находим:
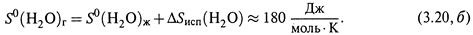 |
г) Кроме того, как и для энтальпии (п. 2.3), употребляются следующие понятия:
ΔS0обр — стандартная энтропия образования вещества X, т. е. изменение энтропии системы в реакции (2.14, а):
простые вещества → X;
ΔS0сг — стандартная энтропия сгорания вещества, относящаяся к реакции (2.14,б):
Х + О2→ оксиды (с макс. СО).
5. Изотермическое расширение и сжатие газа.
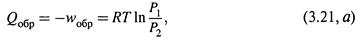 |
а) Если допустить, что процесс идет обратимо, и использовать формулы (1.8) и (1.6):
то изменение энтропии определяется выражением:
 |
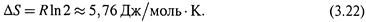 |
Пример. При расширении газа в 2 раза (т.е., если Р1/P2 = 2), в расчете на 1 моль,
б) Но и при необратимом способе расширения изменение энтропии будет точно таким же! Это следует из того, что энтропия — функция состояния. Следовательно, формула (3.21,б) справедлива, независимо от способа расширения (или сжатия) газа. В частности, ею можно пользоваться при расчете ΔS в следующих двух ситуациях, эквивалентных расширению газа в пустоту.
I... Газ занимает объем V1, а ему дают возможность занять больший объем
V2 . Если в дополнительном объеме (V2 – V1) вначале газа не было (т.е. Р = 0), то при расширении газ не совершает никакой работы. Но энтропия его увеличивается, согласно формуле (3.21,б).
II.Аналогичная ситуация наблюдается при смешении разных газов.
6. Изотермическое изменение концентрации раствора.
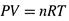 |
а) Для газов давление и концентрация прямо связаны друг с другом. Действительно, из уравнения Клайперона-Менделеева
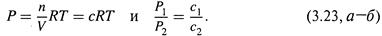 |
следует:
Поэтому, вновь исходя из (3.21,б), для изменения энтропии при изменении концентрации газа от с1 до с2 получаем формулу:
 |
б) Разбавленные растворы во многом подобны газам. Во всяком случае, энергетический беспорядок системы (т.е. энтропия) при разбавлении или концентрировании растворённого вещества должен меняться точно так же, как при сгущении или разрежении газа.
Следовательно, и здесь ΔS рассчитывается по формуле (3.24).
В частности, если с2 < с1 (концентрация уменьшается), то ΔS > 0: энтропия (в расчете на моль вещества) возрастает, так как молекулы получают возможность располагаться более произвольно. Причем при разбавлении вещество не совершает работы, поскольку давление системы при этом не меняется, т.е. процесс эквивалентен расширению газа в пустоту.
Таким образом, изменение концентрации растворенных веществ (для достаточно разбавленных растворов и при постоянной температуре) не сопровождается поглощением или выделением теплоты (в том случае, конечно, когда вещество не взаимодействует с растворителем).
Дата добавления: 2016-03-20; просмотров: 768;
