Изолированные системы

1. В изолированных системах, как известно, исключён обмен энергией с окружающей средой. Поэтому в неравенстве (3.31), выражающем второе начало термодинамики, следует положить

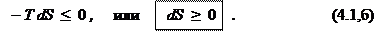откуда

Таким образом, здесь остается только 1 стимул — увеличение энтропии. Самопроизвольными являются лишь процессы, ведущие к увеличению общей энтропии.

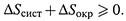2. Вселенная в целом, как уже отмечалось в (п. 1.1), — изолированная система. Получается, что все самопроизвольные процессы ведут к увеличению общей энтропии Вселенной.Этот вывод не нов, поскольку данное утверждение постулировалось неравенством (3.3):

Cправедливости ради заметим, что, видимо, во Вселенной возможны и процессы, дающие обратный результат — концентрацию огромных количеств энергии и массы в небольших объемах пространства.

4.2. Закрытые системы: изотермо-изохорные процессы

1. а) Известно (п. 1.1), что компоненты химической реакции можно рассматривать как закрытую систему. Кроме того, многие реакции (особенно биологические) проходят при постоянной температуре.

Поэтому ситуации, которые предстоит рассмотреть в этом и в следующем пунктах, являются для химика и биолога наиболее важными.

б) Вследствие постоянства температуры, выражение второго начала термодинамики можно записать в данном случае в интегральном виде:

в) Кроме температуры, во многих процессах остается постоянным какой-либо другой ключевой параметр — объем или давление. В этих случаях критерий (4.2) еще несколько модифицируется.

2. а) Пусть постоянным является объем. Работа против давления тогда не совершается. В отсутствие какой-либо иной работы теплота процесса, в соответствии с (1.11,б), равна изменению внутренней энергии:

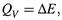
вследствие чего неравенство (4.2) превращается в следующее:

б) А это позволяет ввести новую функцию состояния — свободную энергию (или просто энергию) Гельмголъца:

в) При постоянной температуре ее изменение равно

т.е. совпадает с левой частью неравенства (4.3).

Следовательно, второе начало термодинамики, применительно к изотермо-изохорным процессам, можно записать так:

г)Итак, самопроизвольными являются такие процессы, в которых энергия Гельмгольца убывает (не возрастает). Введение особой функции позволяет, как и для изолированных систем, пользоваться лишь одним — в данном случае суммарным — критерием для исследования способности системы к процессам.

Однако этот чисто формальный прием не отменяет того факта, что на самом деле для самопроизвольных процессов по-прежнему остаются те же два стимула; просто через ΔA обозначен их баланс.

4.3. Закрытые системы: изотермо-изобарные процессы

Ещё более важны для нас изотермо-изобарные процессы.

а) Из-за постоянства температуры интегральная форма второго начала термодинамики остаётся справедливой и здесь:

б) Однако теперь теплота, в соответствии с (2.8), равна изменению энтальпии:

Q_p = ΔЕ + P ΔV = ΔН

(при условии, что не совершается никакой иной работы, как против давления).

в) Подстановка в (4.2) приводит к неравенству:

что даёт основание к введению ещё одной функции состояния – пожалуй, наиболее важной в химии – энергии Гиббса (или свободной энергии Гиббса):

G ≡ H – T S . (4.7,a)

Как и в случае энергии Гельмгольца, смысл такого определения состоит в том, что при постоянной температуре изменение введённой функции

совпадает с левой частью соответствующего неравенства – в данном случае, (4.6).

г) В итоге получается единый, но опять-таки суммарный, критерий:

Данное выражение означает, что в изотермо-изобарных условиях самопроизвольными являются такие процессы, в которых функция Гиббса убывает (не возрастает). Но опять-таки, ΔG – лишь баланс всё тех же двух стимулов: выделения теплоты и возрастания энтропии.

<8 9 101112 13 14 >

Дата добавления: 2016-03-20; просмотров: 681;