Статистическая природа энтропии
Конкретизируем представление об энтропии как о мере энергетического беспорядка.
1. Для этого введём два понятия – макро- и микросостояния системы:
а)макросостояниехарактеризуется макропараметрами – температурой, давлением, объемом, внутренней энергией и т.д.;
б)микросостояние— это конкретное расположение отдельных частиц (молекул) в данный момент времени, а также их скорости и взаимодействия.
Очевидно, что одно и то же макросостояние может реализоваться множеством различных микросостояний. Поэтому для каждого микросостояния существует определенная вероятность piтого, что система находится именно в данном микросостоянии.
Ясно, что S pi= 1.
2. а) Статистическая физика доказывает, что энтропия с точностью до постоянного множителя — это средний логарифм вероятностей микросостояний (возможных при данном макросостоянии), взятый с обратным знаком:
 |
где Ω — общее число возможных микросостояний.
б) Согласно приведенной формуле, величину беспорядка в системе определяют два фактора.
I. Первый – число микросостояний (Ω): чем оно выше, тем больше членов в сумме (3.25) и, следовательно, меньше средняя вероятность, приходящаяся на один член. Ясно, что при этом выше и беспорядок в системе.
II. Второй фактор — то, насколько микросостояния различаются по своей вероятности pi: чем ближе микросостояния по вероятности, тем беспорядок больше. А если все pi одинаковы, то (при одном и том же Ω) энтропия максимальна.
3. а) Последний случай (равновероятность всех микросостояний: все pi = p) обычно реализуется для системы из очень большого числа частиц, и тогда остается влияние только одного фактора — числа микросостояний (Ω), которое теперь очень просто связано с вероятностью микросостояния:
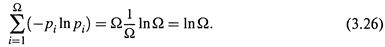 |
б) Выполним для данного случая простые преобразования:
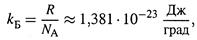 |
в) Наконец, заметим, что коэффициент А в формуле (3.25) — это константа Болъцмана:
имеющая, как видим, размерность энергии (отнесенной к температуре и одной частице). Следовательно, с ее помощью совершается переход от просто «беспорядка» системы к «энергетическому беспорядку».
 |
г) В итоге, для системы с равновероятными микросостояниями получаем знаменитую формулу Больцмана:
 или, в расчете на 1 моль частиц,
или, в расчете на 1 моль частиц,
 |
Как видно, абсолютная энтропия системы просто связана с числом возможных микросостояний.
д) Изменение же энтропии в процессе определяется изменением этого числа:
 |
4. Для иллюстрации представления о микросостояниях обычно приводят следующий пример.
а) В системе — N молекул. Каждая из них характеризуется в некий момент времени координатами хi, yi, zi и энергией Еi.
Вместе эти 4 значения образуют точку в 4-мерном координатно-энергетическом пространстве.
 |
б) Данное пространство определенным образом разбивается на т ячеек. Если допустить, что каждая частица с равной вероятностью может находиться в любой из ячеек, тогда общее число микросостояний можно рассчитать по формуле:
Так, если N = 10 частиц, а m = 5 ячеек, то
 |
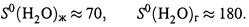 |
5.Для оценки множества микросостояний реальной системы применим формулу Больцмана к воде. Используем оценки (3.20,а-б) абсолютной энтропии воды и пара (в Дж/моль·К) при 25° С:
Подстановка этих величин в (3.27,б) даёт: число микросостояний в расчёте на 1 моль частиц равно
 |
Получается, что на 6·1023 частиц 1 моля жидкой воды при 25° С имеется меньше 5000 равновероятных микросостояний. В газообразном макросостоянии число микросостояний почти на 6 порядков выше.
Дата добавления: 2016-03-20; просмотров: 1040;
