Бинарные операции 02↦ 0 алгебры композиций поворотов квадрата
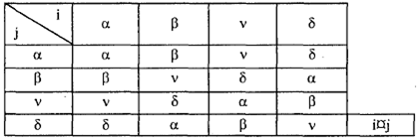
Такая таблица (см. табл. 2), задающая бинарную операцию, называется таблицей Кэли.
Можно представить бинарной операцией, например, смешивание красок, когда из двух цветов получается третий, входящий во множество всех цветов.
Пусть А = <М, φ 2> — группоид. Обозначим, как и в предыдущем примере, φ 2символом ¤.
Тогда элемент n ∈ M называется правым нейтральным элементом группоида А, если для всякого m ∈ M выполняется равенство m ¤ n = m .
Для левого нейтрального элемента выполняется равенство n ¤ m = m .
В дальнейшем для краткости вместо слов «все», «всякий» будем использовать символ V (перевернутая буква ∀ — первая буква английского слова All — все, этот символ называется еще квантором общности ; квантор существования обозначается ∃ и означает «существует», «имеется», «есть»).
Элемент n , являющийся одновременно и левым, и правым нейтральным элементом, называют двухсторонним нейтральным элементом или просто нейтральным элементом.
Для смешивания красок нейтральный элемент — бесцветный лак.
Если группоид <М, ¤> мультипликативный, т. е. его бинарная операция ¤ имеет тип умножения (·), то нейтральный элемент называется единицей и обозначается 1. Если группоид аддитивный, т. е. бинарная операция ¤ имеет тип сложения (+), то нейтральный элемент называется нулем и обозначается 0. Нейтральный элемент в группоиде всегда единственный.
Коммутативный группоид, т. е. группоид, в котором
( ∀ x , у ∈ М) (х ¤ у = у ¤ х),
называется коммутативным или абелевым.
Группоид, в котором выполняется закон ассоциативности
( ∀ x , у, z ∈ М) (х ¤ (у ¤ z ) = (х ¤ у) ¤ z ),
называется ассоциативным или полугруппой.
Полугруппа с единицей называется моноидом . В алгебре поворотов квадрата (см. табл. 2) единицей служит поворот на нулевой угол (α).
Группой называется полугруппа с единицей, в которой для каждого элемента а существует элемент а–1, называемый обратным (а ¤ а–1= а–1 ¤ а = n ), и каждое из уравнений а ¤ х = b , у ¤ а = b обладает единственным решением.
В алгебре поворотов квадрата (см. табл. 2), являющейся группой, обратным к данному повороту является поворот, дополняющий его до 2π:
Группа, все элементы которой являются степенями одного элемента а, называется циклической . Циклическая группа всегда абелева.
Множество рациональных чисел, не содержащее нуля, с операцией умножения является абелевой группой. Обратным к элементу а является элемент 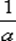 .
.
Дата добавления: 2016-02-24; просмотров: 1224;
