Подграфы и части графа. Операции над графами

Граф G ' = á M ', R ' ñ называется подграфом графа G = á M , R ñ , если M ' ⊆ М и R ' = R ∩ (М ')2. Граф G ' называется частью графа G , если М ' ⊆ М и R ' ⊆ R ∩ (М ')2.

Пример 2.1.Граф G ' = á {1,2,3}, {[1,2], (1,3), [2,3] ñ (рис. 4.9 б ) является подграфом графа G = {{1, 2, 3, 4}. á [1, 2], (1, 3), [1, 4], [2, 3], [3, 4]} ñ (рис. 4.9 а ),а граф G " = á {1, 2, 3}, {[1, 2], (3, 2)} ñ (рис. 4.9 в ) — частью графа G .

Рассмотрим некоторые основные операции, производимые над графам».

Операцией добавления к графу G = á M , R ñ вершины а образуется граф á {М ∪ {а }, R ñ . Операция добавления дуги ( a , b ) к графу G состоит в образовании графа á М ∪ {а , b }, R ∪ {( a , b )} ñ . Под операцией удаления дуги ( a , b ) яз графа G понимается операция, заключающаяся в удалении пары ( a , b ) из множества дуг R в результате получается граф á {М , R ( a , b )} ñ . Операция удаления вершины а из графа G заключается в удалении вершины a вместе с инцидентными ей дугами:

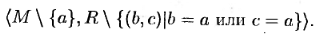
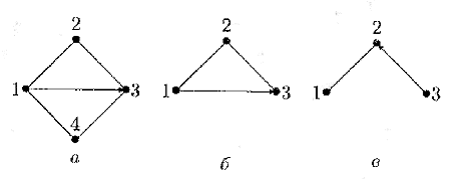
Рис. 4.9

Операция отождествления вершин а и b графа G = á M , R ñ состоит в удалении из графа G вершин а и b и присоединении новой вершины а ', дуг (а ', с ), если (а , с ) ∈ R или ( b , с ) ∈ R , и дуг (с , а '), если (с , а ) ∈ R или (с , b ) ∈ R :

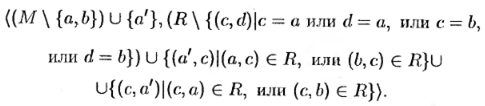
Говорят, что построенный граф получается из графа G отождествлением вершин a и b . В случае, когда a и b соединены дугой, операцию отождествления вершин а и b называют стягиванием дуги (а , b ).

Пример 2.2.Из графа G . показанного на рис. 4.10, добавлением вершины 5 образуется граф G 1, добавлением дуги (3,1) — граф G 2, удалением дуги (3, 2) — граф G 3, удалением вершины 2 — граф G 4, отождествлением вершин 1 и 4 — граф G 5, стягиванием дуги (2,3) — граф G 6.

Дополнением графа без петель G = á M , R ñ называется граф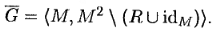

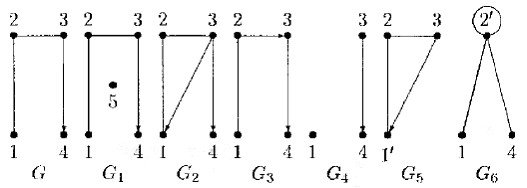
Рис. 4.10

Маршруты

Пусть G = á M , R ñ — граф. Последовательность

a 1, u 1, a 2, u 2, …, un, an+1 (4.1)

где a 1, a 2, …, an+1∈ М , u 1, u 2, …, un∈ R , называется маршрутом , соединяющим вершины a 1 и ап+1(( a 1, ап + 1 )-маршрутом ), если ui= ( ai, ai + 1 ), i = 1, 2,..., п (рис. 4.18).

Очевидно, что маршрут (4.1) можно задать последовательностью a 1,…, ап + 1 его вершин, а также последовательностью u 1, …, u пдуг. Число п дуг в маршруте (4.1) называется его длиной .

Пусть G — неорграф. Маршрут (4.1) называется цепью , если все ребра [ a 1, a 2],..., [ an, an+1] различны, и простой цепью , если все его вершины кроме, возможно, первой и последней, различны. Маршрут (4.1) называется циклическим , если a 1= an+1. Циклическая цепь называется циклом , а циклическая простая цепь — простым циклом . Неорграф без циклов называется ациклическим . Минимальная из длин циклов неорграфа называется его обхватом .

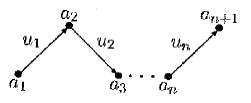
Рис. 4.18

Пример 3.1.Рассмотрим граф, изображенный на рис. 4.19. В нем на боры (1, 2), (1, 2, 4, 7), (3, 4, 5, 6) являются простыми цепями; (1, 2, 4, 7, 8, 4) — цепь, не являющаяся простой; (1,4,7,8,4. 2) — маршрут, не являющийся цепью; (1, 2, 4, 7, 8, 4, 1) — цикл, не являющийся простым: (1, 2, 4, 1) — простой цикл. Обхват этого графа равен 3.

Пусть G — граф, возможно, ориентированный. Маршрут (4.1) называется путем , если все его дуги различны. Путь (4.1) называется контуром , если a 1= an+1. Граф, не имеющею контуров, называется бесконтурным . Вершина b называется достижимой из вершины а , если существует (а , b )-путь.

Степени вершин

Степенью или валентностью вершины а неорграфа G называется число ребер, инцидентных вершине а , т. е. число ребер, концом которых является вершина а (при этом петли считаются дважды). Если G — орграф, то степени его вершин определяются как степени вершин в соответствующем неорграфе F ( G ). Аналогично вводится понятие степени вершины в мулътиграфах. Степень вершины a будем обозначать через degGa или просто deg a . Вершина степени 0 называется изолированной , вершина степени 1 — концевой или висячей .

Пример 6.1.Вершины графа G , изображенного на рис. 4.28, имеют следующие валентности: deg l = deg 2 = deg 3 = 1 (т. е. l , 2, 3 — висячие вершины), deg 4 = 5, deg 5 = 0 (т. е. 5 — изолированная вершина).

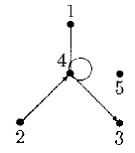
Рис. 4.28

Рассмотрим сумму степеней всех вершин графа. Поскольку каждое ребро входит и эту сумму дважды, справедливо

Утверждение 6.1(лемма о рукопожатиях). Сумма степеней всех вершин графа , является четным числом и равна удвоенному числу ребер .

Пусть G — бесконтурный орграф. Полустепенью исхода deg +а вершины а называется число дуг, исходящих из а . Полустепенью захода deg –а вершины а называется число дуг, которые заходят в вершину а . Справедливо соотношение deg a = deg +a + deg –a .

Раскраски графов

Пусть G = á M , R ñ — неограф без петель. Pac краской (вершин ) графа G называется такое задание цветов вершинам G , что если [а , b ] ребро, то вершины а и b имеют различные цвета. Хроматическим числом χ ( G ) графа G называется минимальное число цветов, требующееся для раскраски G .

Пример 14.1.Так как в полном графе Кплюбые две различные вершины связаны ребром, то χ (Кп) = п .

Многие: практические задачи сводятся к построению раскрасок графов.

Пример 14.2.1. Рассмотрим задачу составления расписания. Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно (например, их читает один и тот же лектор). Построим граф G , вершины которого биективно соответствуют лекциям и две вершины смежны тогда и только тогда, когда соответствующие им лекции нельзя читать одновременно. Очевидно, что любая раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам одного цвета, могут читаться одновременно. Напротив, любое допустимое расписание определяет раскраску графа G . Оптимальные расписания соответствуют раскраскам с минимальным числом цветов, а число часов, необходимое для прочтения всех лекций, равно χ ( G ).

2. Рассмотрим граф G , вершины которого — страны, а ребра соединяют страны, имеющие общую границу. Числу χ ( G ) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет.

Существуют и практические задачи, связанные с раскраской ребер в мультиграфе.

Раскраска ребер в мультиграфе G может быть определена с помощью раскраски вершин так называемого реберного мультиграфа. L ( G ). Для произвольного неориентированного мультиграфа G = á M , U , P ñ реберным мулътиграфом L ( G ) называется тройка á U , М , Р ' ñ , где Р ' ⊆ U × M × U , и выполняется ( u , a , v ) ∈ Р ' тогда и только тогда, когда в мультиграфе G вершина, а является концом ребер и и v . Раскраской ребер мультиграфа G называется раскраска вершин мультиграфа L ( G ).

Пример 14.3.Проводится монтаж аппаратуры. Чтобы не перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а ребрами — проводники.

Неорграф G называется бихроматическим , если χ ( G ) = 2. Неорграф G = á М , R ñ называется двудольным , если множество всех ребер графа G образует разрез графа G , т. е. для некоторого разбиения множества вершин {М 1, М 2} концы любого ребра принадлежат разным частям разбиения.

Теорема 14.1.Пусть G — неорграф без петель , имеющий хотя бы одно ребро . Тогда следующие условия эквивалентны:

1. G — дихроматический граф;

2. G — двудольный граф;

3. G не содержит , циклов нечетной длины .

Следствие 14.2.Если G — лес , то χ ( G ) ≤ 2.

Оценим хроматическое число графа G через его параметры. Обозначим через deg ( G ) максимальную степень вершин графа G .

Теорема 14.3.Для любого неорграфа G без петель выполняется неравенство χ ( G ) ≤ deg ( G ) + 1.

Рассмотрим простой алгоритм построения раскраски, который во многих случаях приводит к раскраскам, близким к минимальным.

Алгоритм последовательной раскраски .

1. Произвольная вершина а 1графа G принимает цвет 1.

2. Если вершины a 1, ..., aiраскрашены l цветами 1, 2, ..., l . l ≤ i , то новой произвольно взятой вершине; ai + 1 припишем минимальный цвет, не использованный при раскраске вершин из множества {а j| p ( ai + 1 , aj) = 1, j < i }.

Для некоторых классов графов последовательная раскраска является минимальной. В общем случае это не так.

Планарные графы

Неорграф G называется планарным , если его можно изобразить на плоскости так, что никакие два ребра не будут иметь общих точек, кроме, может быть, общего конца этих ребер. Такое изображение графа на плоскости называется плоским . Таким образом, если граф имеет плоское изображение, то он является планарным.

Пример 15.1. Граф К 4(рис. 4.48а) планарен, поскольку может быть изображен, как показано па рис. 4.48 б .

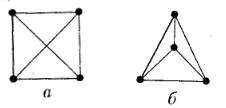
Рис. 4.48

Граф, описанный в примере 14.2 является планарным. Также планарным является граф, вершины которого — отверстия печатной платы, а ребра — проводники печатной платы, соединяющие отверстия.

Рассмотрим операцию подразбиения ребра в графе G = á М , R ñ . После подразбиения ребра [ a , b ] ∈ R получается граф G ' = á М ', R ' ñ , где М ' = М ∪ [ a , b ], R ' = ( R {[ a , b ]) ∪ {[ a , ab ], [ ab , b ]}, т. е. ребро [ a , b ] заменяется на ( a , b )- цепь длины два. Два графа называются гомеоморфными , если их можно получить из одного графа с: помощью последовательности подразбиений ребер.

Не всякий неорграф является планарным. Критерий планарности описывает

Теорема 15.1(теорема Понтрягина — Кураторского). Граф G планарен тогда и только тогда , когда G не содержит подграфа , гомеоморфного К 5или К 3,3(рис. 4.49 ).

Эквивалентная форма критерия планарности описана в следующей теореме.

Теорема 15.2.Тогда и только тогда неорграф G планарен , когда G не содержит подграфов , стягиваемых (т . е . получаемых последовательностью отождествлений вершин , связанных ребрами) к графу К 5или К 3, 3(рис. 4.49 ).

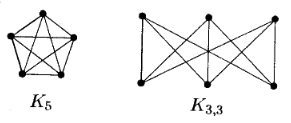
Рис. 4.49

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов , Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ , 2003. — С. 114–124 , 130–131 , 153–154. — (Серия «Высшее образование»).

Изоморфизм графов

Для ориентированного графа (V , Е ) множество Е дуг можно рассматривать как график бинарного отношения непосредственной достижимости , заданного на множестве вершин .

В неориентированном графе (V , Е ) множество Е ребер является множеством неупорядоченных пар. Для каждой неупорядоченной пары {u , v } ∈ Е можно считать, что вершины u и v связаны симметричным бинарным отношением ρ , т. е. {u , v } ∈ ρ и {v , u } ∈ ρ .

Таким образом, с каждым неориентированным и ориентированным графом связано бинарное отношение ρ . Это отношение будем называть отношением смежности .

С алгебраической точки зрения как ориентированный, так и неориентированный граф можно рассматривать как модель , сигнатура которой состоит из одного бинарного отношения : 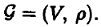В классической теории графов изучаются преимущественно конечные модели такого рода.

При указанном подходе различия между ориентированным и неориентированным графами проявляется только в свойствах отношения смежности ρ . Если это отношение симметрично , то граф называют неориентированным, и с этой точки зрения неориентированный граф можно считать частным случаем ориентированного.

Применяя к данному частному случаю моделей общие понятия гомоморфизма и изоморфизма …, мы можем сформулировать следующие определения.

Определение 5.14. Отображение h : V 1→ V 2множества вершин графа G 1= (V 1, ρ 1) в множество вершин графа G 2= (V 2, ρ 2) называют гомоморфизмом графов (графа G 1в граф G 2), если для любых двух вершин, смежных в первом графе, их образы при отображении h смежны во втором графе, т. е. если

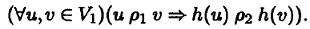
Биективный гомоморфизм h , такой, что любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т. е.

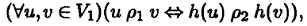
называют изоморфизмом графов G 1и G 2(графа G 1на граф G 2), а графы G 1и G 2— изоморфными , что записывают в виде G 1≅ G 2.

Гомоморфизм графов, который является эпиморфизмом , называется также гомоморфизмом одного графа на другой.

Возвращаясь к нашему определению графа посредством двух множеств: множества вершин V и множества ребер (дуг) Е , получим следующие варианты определений гомоморфизма и изоморфизма.

Гомоморфизм неориентированного графа G 1= (V 1, Е 1) в неориентированный граф G 2= (V 2, Е 2) есть такое отображение h : V 1→ V 2, что для любых двух вершин первого графа, соединенных ребром, их образы при отображении h также соединены ребром, т. е.

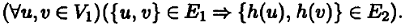
Гомоморфизм ориентированного графа G 1= (V 1, Е 1) в ориентированный граф G 2= (V 2, Е 2) есть такое отображение h : V 1→ V 2, что для любых двух вершин u , v первого графа, таких, что есть дуга, ведущая из u в v , из вершины h (u ) тоже ведет дуга в h (v ), т. е.

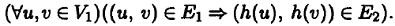
Изоморфизм неориентированного графа G 1на неориентированный граф G 2есть такая биекция h : V 1→ V 2, при которой две вершины u и v графа G 1соединены ребром тогда и только тогда, когда соединены ребром их образы h (u ) и h (v ), т. е.

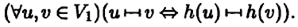
Аналогично изоморфизм ориентированного графа G 1на ориентированный граф G 2есть такая биекция h : V 1→ V 2, при которой в ориентированном графе G 1из вершины u ведет дуга в вершину v тогда и только тогда, когда в ориентированном графе G 2из образа h (u ) вершины и ведет дуга в образ h (v ) вершины v , т. е.

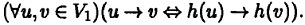
Цит. по: Дискретная математика: учебник для вузов /
А.И. Белоусов , С.Б. Ткачев; под ред. В.С. Зарубина , А.П. Крищенко. —
3-е изд. , стереотип. — М.: Изд-во МГТУ им. Баумана , 2004. — С. 341–343. —
(Сер. Математика в техническом университете; Вып. XIX).

Говорят также: упорядоченная п-ка (например, упорядоченная тройка, четверка, пятерка и т. д.).

Нефедов В.Н.Курс дискретной математики / В.Н. Нефедов, В.А. Осипова. — М: Издательство МАИ, 1992. — 264 с.

Нефедов В.Н.Курс дискретной математики / В.Н. Нефедов, В.А. Осипова. — М: Издательство МАИ, 1992. — 264 с.

Непорожнев И.П.Элементы дискретной математики / Учеб.-метод. пособие. — Пермь: ПВВКИКУ, 1994. — 38 с.

Нефедов В.Н.Курс дискретной математики / В.Н. Нефедов, В.А. Осипова. — М: Издательство МАИ, 1992. — 264 с.

При таком подходе в неориентированном графе могут быть петли , если отношение р содержит некоторые элементы диагонали , в частности является рефлексивным .