Основные показатели сетевого графика.

Определение 4.6. Ранним временемнаступления события х iназывается длина максимального пути L (х 0, х i) от начала всех работ до момента х i. Длина пути | L (х 0, х i)| определяется как сумма длин всех его дуг. Обозначим раннее время

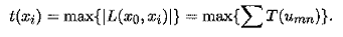
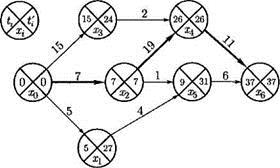
Рис. 4.14. Сетевой график

По определению, t ( x 0) = 0. Раннее время момента завершения всех работ t ( xk) = t * называется критическим временемсетевого графика, а путь L (х 0, х k) = L * , длина которого равна критическому времени, называется критическим путемсетевого графика.

Пример 4.7. Всетевом графике на рис.4.14 проведем расчет ранних времен всех вершин и занесем результаты расчета в левые четверти кружков, изображающих вершины. Так для вершин х 4, х 5, х 6будем иметь:

t ( x 4) = max {17,26} = 26, t ( x 5) = m ах{8,9} = 9, t ( x 6) = m ах{28,37,14,15} = 37.

Чем ближе очередная вершина графика к конечной вершине, тем большее число путей от начала и длиннее каждый путь надо рассматривать. Этого можно избежать, если вести расчет ранних времен по формуле прямой волны:

t (xi) = max{t (xm) + T (umi)}.

В этой формуле рассматривается для всех соседних к xiпредшествующих вершин хтнаибольшая из сумм раннего времени вершины-соседки и длительности работы от нее до заданной вершины. Например, если уже известны ранние времена t ( x 4)= 26 и t ( x 5) = 9 (см. рис. 4.14), то легко найти t ( x 6) = max {(26 + 11), (9 + 6) = 37}. Расчет ранних времен ведется по этой формуле от начальной вершины к конечной подобно распространению прямой волны (см. рис. 4.14). В конце расчета получаем критическое время t * = t ( x 6) = 37 и критический путь L *( x 0, x 6) = { u 02, u 24, u 46} сетевого графика. Критический путь на рис. 4.14 выделим.

Определение 4.7. Поздним временемнаступления события х iназывается разность критического времени t * сетевого графика и длины максимального пути L *( xi, xk) от момента xiдо момента окончания всех работ. Обозначим позднее время

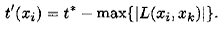
По определению имеем для конечной вершины

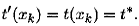
Так, для вершины х 2сетевого графика на рис. 4.14 получаем:

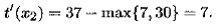
Таблица 4.1