Определение и примеры графов

Определение 4.1.Графом называется Г = á X , R ñ , где X — произвольное множество элементов, называемых вершинами , R ⊆ X × X = X 2— бинарное отношение между элементами множества X , т. е. R — некоторое множество пар вида ( xi, xj), где xi, xj∈ X .

Пары из R называются дугами графа, причем считается, что дуга ( xi, xj) имеет направление от xiк xj, т. е. от первого элемента в упорядоченной паре ко второму. При этом говорят, что дуга ( xi, xj) инцидентна вершинам xi, xj. Дуга вида ( xi, xj) называется петлей .

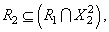Граф Г1, составленный из части вершин и части дуг другого графа Г2, таких, что называется подграфом второго, и пишут: Г1⊆ Г2.

Последовательность дуг ( xi, xj);( xj, xl); ...;(хт, хп), таких, что конец любой дуги кроме последней совпадает с началом следующей дуги, называется путем в графе. При этом будем предполагать, что все вершины дуг пути, кроме, возможно, первой и последней, различны. Число дуг пути называется его длиной . Путь обозначается L ( xi, xn), где вершины xi, xnназываются началом и концом пути, а остальные вершины — промежуточными .

Если путь в графе имеет совпадающие начало и конец, то он называется циклом .

Итак, граф — это вершины и дуги. Геометрически они изображаются следующим образом. Рассмотрим произвольное множество Q точек плоскости, мощность которого равна мощности множества X . Сопоставим любым образом взаимно-однозначно множества X и Q . Для каждой дуги ( xi, xj) графа найдется пара точек qiи qjиз Q . Соединим эти точки произвольной непрерывной кривой (дугой), направленной от qiк qj.

На плоскости появится рисунок, который является геометрическим изображением графа.

Если две вершины qi, qjсоединены дугами в оба направления, т. е. имеются обе дуги ( qi, qj) и ( qj, qi), то часто такие вершины соединяют одной линией (ребром) без направления. Ребро заменяет две дуги противоположного направления.

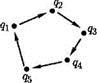
Рис . 4.1. Циклический граф

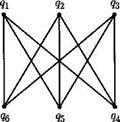
Рис . 4.2. Симметричный граф K 3,3

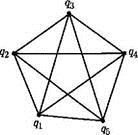
Рис . 4.3. Полный граф K 5

Определение 4.2.Граф Г = á X , R ñ , у которого бинарное отношение R — симметричное, называется симметричным (неориентированным). Все остальные графы называются несимметричными (ориентированными).

Пример 4.1. Граф, изображенный на рис. 4.1, называется циклическим .

Пример 4.2. Симметричный граф на рис. 4.2 обозначается K 3,3изображен с использованием ребер без направлений.

Пример 4.3. Симметричный граф называется полным , если любые две его вершины соединены между собой ребром. На рис. 4.3 изображен полный граф, обозначаемый K 5.

Часто возникает ситуация, когда две вершины требуется соединить произвольным числом дуг. Тогда используют более общее понятие, чем граф, мультиграф. Мулътиграфом называются два множества á X , U ñ и матрица В . Здесь X — множество т вершин, U — множество п дуг и матрица В размером т × п , называемая матрицей инцидентности . Матрица инцидентности показывает, какая дуга имеет какую вершину начальной, а какую конечной. В матрице инцидентности номера строк соответствуют номерам вершин, а номера столбцов — номерам дуг. Элемент bijматрицы инцидентности задается по формуле

Отметим, что любой граф можно задать как мультиграф с единичной кратностью дуг.