Отношения эквивалентности и разбиения. Фактор-множества

Отношение Р называется отношением эквивалентности (эквивалентностью ), если Р рефлексивно, симметрично и транзитивно. Эквивалентности часто обозначают символами Е и ~ (тильда ): хЕу , х ~ у .

Пример 6.1.1. Отношение равенства х = у является эквивалентностью на любом множестве А , так как оно рефлексивно (х = х ), симметрично (х = у ⇒ у = х ) и транзитивно (х = у , y = z ⇒ x = z ).

2. Отношение подобия на множестве треугольников есть отношение эквивалентности.

3. На любом множестве Ƥ ( U ) отношение равно мощности |А | = | B | является отношением эквивалентности.

4. Отношение принадлежности к одной студенческой группе на множество студентов НГТУ — отношение эквивалентности.

5. Рассмотрим множество М программ, вычисляющих некоторые функции. Отношение Е = {(х ,у ) | программы x и у вычисляют одну и ту же функцию f является эквивалентностью.

Пусть Е — эквивалентность на множестве А . Классом эквивалентности элемента х ∈ А называется множество Е (х ) = {у | хЕу }. Классы эквивалентности Е будут также называться Е-классами . Множество A / E = {Е (х ) | х ∈ А } называется фактор-множеством множества А по отношению Е .

Пример 6.2.1. Для отношения равенства = на множестве А каждый = класс состоит только из одного элемента: = ( x ) = { x } для любого х ∈ А . Таким образом, фактор-множество А /= имеет вид {{х } | х ∈ А ] и, следовательно, биективно множеству А .

2. Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы. Фактор-множество множества студенток НГТУ по этому отношению эквивалентности представляет собой множество студенческих групп НГТУ.

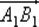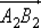Пример 6.4.Рассмотрим геометрическое векторное пространство E 3и множество направленных отрезков в нем. Направленные отрезки и называются эквивалентными : 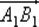~ 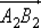, если они имеют одинаковые длину и направление. Отношение ~ — это отношение эквивалентности.

Вектором (геометрическим вектором .) 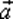в Е 3называется класс эквивалентности направленных отрезков 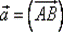для некоторого 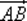). Фактор-множество множества направленных отрезков по отношению ~ образует множество векторов пространства Е 3.

Отношения порядка

Отношение эквивалентности является обобщением отношения равенства: эквивалентные элементы считаются «равными». Обобщением обычного отношения ≤ служат отношения порядка.

Отношение Р ⊆ А 2называется предпорядком или квазипорядком , если Р рефлексивно и транзитивно.

Пример 7.1.Отношение Р = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (1, 3)} на множество {1, 2, 3} является предпорядком (рис. 1.11).

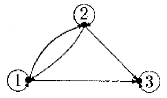
Рис. 1.11.

Отметим, что симметричный предпорядок является отношением эквивалентности.

Отношение Р ⊆ А2называется частичным порядком , если Р рефлексивно, транзитивно и антисимметрично. Таким образом, частичный порядок — это антисимметричный предпорядок. Частичный порядок обычно обозначается символом ≤, а обратное ему отношение ≤–1 — символом ≥. Отношение ≥ также является частичным порядком и называется двойственным порядку ≤. Используя отношение ≤, определим отношение <, называемое строгим порядком, по следующему правилу: х < у ⇔ х ≤ у и х ≠ у . Заметим, что отношение строгого порядка не является частичным порядком, так как не выполняется условие рефлексивности (неверно, что х < х ).

Пример 7.2.Частичным порядком является обычное отношение ≤ на множестве ℕ . Действительно, это отношение рефлексивно (х ≤ х ), транзитивно (х ≤ у, у ≤ z ⇒ х ≤ z ) и антисимметрично (х ≤ у, у ≤ x ⇒ х = y ).

Пример 7.3.Отношение, изображенное на рис. 1.12, является частичным порядком, а отношение из примера 7.1 — нет.

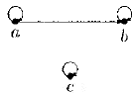
Рис. 1.12

Пример 7.4 . Отношение включения ⊆ на булеане Ƥ ( U ) образует частичный порядок.

Заметим, что в примерах 7.3 и 7.4 имеются элементы х и у , про которые нельзя сказать, что х ≤ у или у ≤ х (например, при а = х , у = с из примера 7.3). Такие элементы называются несравнимыми. Частичный порядок ≤⊆ А 2 называется линейным порядком , если любые два элемента х и у из множества A сравнимы, т. е. х ≤ у или у ≤ х (линейным является частичный порядок из примера 7.2).

Непустое множество А , на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно ) упорядоченным множеством (сокращенно ч.у.м. или л.у.м.).

Пример 7.5. Пары á ω , ≤ñ , á [0, 1], ≤ñ с обычными отношениями ≤ образуют линейно упорядоченные множества.

Пусть á А , ≤ñ — частично упорядоченное множество. Определим на множестве А 2отношение П условием ( a 1, b 1) П ( a 2, b 2) ⇔ a 1 ≤ a 2 и b 1 ≤ b 2.Отношение П есть отношение частичного порядка. Оно называется отношением Парето. Пара á A 2, П ñ образует частично, по не линейно упорядоченное множество, если |А | > 1.

Элемент a ∈ А частично упорядоченного множества 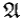= á А , ≤ñ называется максимальным (минимальным ), если для всех х ∈ А из a ≤ х (х ≤ a ) следует x = а . Элемент a ∈ А называется наибольшим (наименьшим), если х ≤ а ( a ≤ х ) для всех х ∈ А . Наибольший (наименьший) элемент ч.у.м. 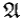(если он существует) обозначается через max 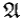( min 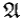). Наибольший элемент часто называют единицей , а наименьший — нулем множества 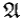. Заметим, что всякий наибольший элемент является максимальным, а всяким наименьший элемент — минимальным. Обратное утверждение, вообще говоря, неверно. Всякое конечное ч.у.м. содержит как максимальные, так и минимальные элементы.

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов , Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ, 2003. — С. 16–19, 34–38. — (Серия «Высшее образование»).