Метод включений и исключений
Пусть множество А имеет N элементов и п одноместных отношений (свойств) Р 1, Р 2, ..., Рп. Каждый из N элементов может обладать или не обладать любым из этих свойств. Обозначим через  число элементов, обладающих свойствами
число элементов, обладающих свойствами  и, может быть, некоторыми другими. Тогда число N (0) элементов, не обладающих ни одним из свойств P 1, P 2, ..., Рп, определяется по следующей формуле, называемой формулой включений и исключений :
и, может быть, некоторыми другими. Тогда число N (0) элементов, не обладающих ни одним из свойств P 1, P 2, ..., Рп, определяется по следующей формуле, называемой формулой включений и исключений :

Пример 5.1.Пусть колода состоит из п карт, пронумерованных числами 1, 2, ..., n . Сколькими способами можно расположить карты в колоде так, чтобы ни для одного i (1 ≤ i ≤ п ) карта с номером i не занимала i -е место?
Имеется п свойств Р iв виде « i -я карта занимает в колоде i - e место». Число всевозможных расположений карт в колоде равно n !. Число  расположений, при которых карта с номером ijзанимает место ij( j = 1, ..., k ), равно ( n – k )!. Тогда S 0= n ! .
расположений, при которых карта с номером ijзанимает место ij( j = 1, ..., k ), равно ( n – k )!. Тогда S 0= n ! .

Используя формулу (5.2), получаем, что число N (0) расположений, при которых ни одно из свойств Piне выполнено, равно
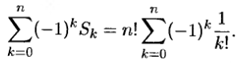
Обобщая формулу (5.2), получаем формулу, позволяющую вычислить число N ( r ) элементов, обладающих ровно r свойствами (1 ≤ r ≤ п ):

Определим функцию [х ] для вещественных чисел х как наибольшее целое число, не превосходящее х . Для положительных целых чисел а и b значение функции  равно количеству чисел из множества {1, 2, ..., b }, которые делятся на а , т. е. кратных a .
равно количеству чисел из множества {1, 2, ..., b }, которые делятся на а , т. е. кратных a .
Пример 5.2.Сколько положительных чисел от 1 до 500 делятся ровно на одно из чисел 3, 5 или 7?
Обозначим свойства делимости на 3, 5 и 7 соответственно через P 1, P 2, и Р 3. Тогда для N = 500 имеем  Так как N 12— число общих кратных для чисел 3 и 5, наименьшее общее кратное которых равно 15, то N 12совпадает с количеством чисел, которые делятся на 15, т. е.
Так как N 12— число общих кратных для чисел 3 и 5, наименьшее общее кратное которых равно 15, то N 12совпадает с количеством чисел, которые делятся на 15, т. е. 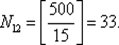
Аналогично  По формуле (5.3) находим искомое число чисел
По формуле (5.3) находим искомое число чисел
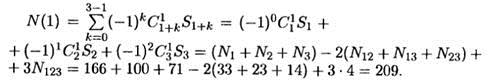
Дата добавления: 2016-02-24; просмотров: 1913;
