Тема 2. Элементы комбинаторики

Комбинаторные вычисления

При решении теоретико-множественных задач большое значение имеет определение мощности конечных множеств.

Очевидно, что | A ∪ В| = |А| + |В| – |А ∩ В|, т. е., когда А и В в «общем положении», т. е. пересекаются.

Кроме того, |А В| = |А| – |В|, когда А включается в В, |А В| = |А| – | А ∩ В|, когда А и В в «общем положении», т. е. пересекаются.

Нетрудно заметить, что |А ⊕ В| = |А| + |В| – 2|А ∩ В|.

В дискретной математике имеется специальный раздел, занимающийся подсчетом и перечислением элементов в конечных множествах — комбинаторика, или комбинаторный анализ. Вычисления на дискретных конечных математических структурах часто называют комбинаторными вычислениями.

Пусть в базе данных имеется n записей об объектах недвижимости (например, квартирах) в виде запроса (что требуется) и предложения (что имеется). Требуется найти такие пары записей, в которых предложение первой записи совпадает с запросом второй и, наоборот, предложение второй записи совпадает с запросом первой («подбор вариантов обмена»).

Допустим, на проверку варианта обмена тратится одна миллисекунда. Можно показать, что при сравнении каждой записи с каждой требуется n ( n – 1) / 2 сравнений.

Например, n = 8:

(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8),

(2,3), (2,4), (2,5), (2,6), (2,7), (2,8),

(3,4), (3,5), (3,6), (3,7), (3,8),

(4,5), (4,6), (4,7), (4,8),

(5,6), (5,7), (5,8),

(6,7), (6,8), (7,8) — всего 28 вариантов: 8 · 7/2 = 28 = 7 + 6 + 5 + 4 + 3 + 2 + 1. Здесь отношение сравнения симметрично и сам с собой вариант не сравнивается.

Если n = 100, то при указанном быстродействии на сравнения уйдет 4,95 с. Но если n = 100000 (в задачах реальной размерности), то необходимо 1999950 с, т. е. без малого 1389 ч. Столько ждать клиент вряд ли будет. Это и есть «проклятие размерности». И это только сравнение прямых вариантов, а существуют варианты, в которых число участников сделки больше двух.

Поэтому комбинаторные вычисления требуют предварительного анализа и ориентировочной количественной оценки исходных данных. Иначе можно подумать, что компьютер просто «завис» и не выдаёт ответа. Здесь речь идет о сложности вычислений в смысле времени решения. В ряде задач комбинаторной сложности необходимо время, сравнимое с геологическими эпохами. Но есть еще и пространственная сложность — в смысле объема памяти. Ведь промежуточные результаты часто надо где-то хранить. В ряде задач требуется объем памяти, превышающий количество атомов во Вселенной.

Основным инструментом такого анализа сложности вычислений и является комбинаторика.

Основные понятия комбинаторики

Основная задача комбинаторики как раздела дискретной математики — пересчет и перечисление элементов в конечных множествах.

Если требуется определить, сколько элементов, принадлежащих заданному конечному множеству, обладает некоторым свойством или заданным набором свойств, то это задача пересчета. Если необходимо выделить все элементы множества, удовлетворяющие заданным свойствам, то это задача перечисления.

В некоторых задачах на исходном конечном множестве элементов определена целевая функция, причем нас интересуют элементы множества, соответствующие минимальному или максимальному значению этой функции. В этом случае решается задача оптимизации.

При этом под решением задачи оптимизации «в сильном смысле» понимается нахождение всех элементов минимизирующих (максимизирующих) целевую функцию, а под решением задачи оптимизации «в слабом смысле» — нахождение единственного произвольного элемента.

Рассмотрим основополагающие правила комбинаторики — правила суммы и произведения.

Пусть X — конечное множество, состоящее из n элементов х. Тогда говорят, что элемент х из X может быть выбран n способами и пишут |Х| = n . Эта запись совпадает с записью мощности множества X .

Пусть X 1,..., Х k— попарно непересекающиеся множества, т. е. Xi∩ Xj= ∅ , i ≠ j .

Очевидно, что в этом случае

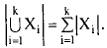
Таково комбинаторное правило суммы. Для k = 2 оно формулируется следующим образом. Если объект х может быть выбран n способами из множества X , а объект y из непересекающегося с ним множества Y — другими m способами, то выбор «х или у» может быть осуществлен n + m способами.

Правило произведения для k = 2 формулируется следующим образом. Если объект х может быть выбран n способами и после каждого из таких выборов объект у в свою очередь может быть выбран m способами, то выбор упорядоченной пары — вектора (х, у) может быть осуществлен n · m способами.

Например, X : { x 1, x 2}, Y : { y 1, y 2}.

Тогда упорядоченные пары (х, у) описываются декартовым произведением

X · Y = {(х1, у1), (х1, у2), (х2, у1), (х2, у2)}.

Выбор упорядоченной последовательности из k объектов вектора (х1, х2, ..., х k) может быть осуществлен n 1 · n 2· ... · nk-способами, где ni— число способов выбора i -г o объекта xi, i меняется от 1 до k (записывается: ).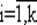

В частности, если все niравны, что может быть, например, в случае, когда элементы принадлежат одному и тому же множеству, т. е. рассматривается декартово произведение Х k, то число способов равно nk.

Набор элементов 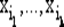из множества X = {х1, ..., х n} (вектор) называется выборкой (комбинацией) объема k из n элементов или, иначе, ( n , k )-выборкой.

Выборка называется упорядоченной , если порядок следования элементов в ней задан. Две упорядоченные выборки, различающиеся лишь порядком следования элементов, считаются различными.

Если порядок следования элементов не является существенным, то такая выборка называется неупорядоченной.

В выборках могут допускаться и не допускаться повторения элементов, т. е. имеются выборки с повторением и выборки без повторений.

Размещения

Упорядоченная ( n , k )-выборка, в которой элементы могут повторяться, называется ( n , k )-размещением с повторениями.

Иными словами, размещениями с повторениями из n элементов по k называют векторы длины k, составленные из n элементов множества X .

Число размещений с повторениями из n элементов по k определяется оценкой соответствующего декартова произведения Х kn -элементного множества, обозначается 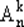(по-видимому от английского слова Assing — назначать) и вычисляется следующим образом:

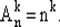
Таким образом, первый элемент вектора длины k выбирается n способами, второй — n способами и т. д.: n · n · ... · n = nk.

Пример.Сколькими способами можно оснастить две различные фирмы компьютерами трех типов?

Каждый способ оснащения есть выборка (3, 2), вектор длины 2, составленный из трехэлементного множества типов Т = { t 1, t 2, t 3}. Поэтому число способов оснащения — число размещений с повторениями из 3 по 2:

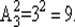
Рассмотрим подробнее:

1) ( t 1, t 1); 2) ( t 1, t 2); 3) ( t 1, t 3)

4) (t2,t2); 5) (t2,t3); 6) (t2,t1);

7) (t3, t3); 8) (t3, t2); 9) (t3, t1).

Получили различные упорядочения двухэлементных векторов из трех элементного множества, т. е. множество Т2.

Здесь каждый вектор соответствует способу оснащения. Видно, что, например, ( tl, t 2), ( t 2, t 1) считаются разными способами, так как фирмы предполагаются различными («первая — первым типом», «вторая — вторым» и т. д.). Имеются повторения: ( tl, t 1), ( t 2, t 2), ( t 3, t 3).

В ряде задач необходимо определить число векторов длины k из n элементов данного множества без повторения элементов.

Если элементы упорядоченной ( n , k )-выборки попарно различны, то они называются ( n , k )-размещением без повторений или просто ( n , k )-размещением.

Число таких размещений без повторений обозначается .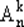

Каждое ( n , k )-размещение без повторения является упорядоченной последовательностью длины k , элементы которой попарно различны и выбираются из множества с n элементами. Тогда первый элемент этой последовательности может быть выбран n способами, после каждого выбора первого элемента последовательности второй элемент может быть выбран ( n – 1)-способами и т. д., k -й элемент выбирается n – ( n – k )-способом:

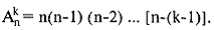
Преобразуем эту формулу, умножая и деля ее на произведение чисел 1 · 2···( n – k ):

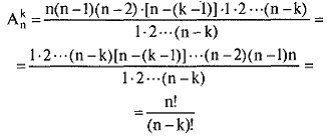
В частности, при k = 0 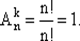Очевидно, что при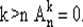

Пример.Сколькими способами можно скомплектовать группу из трех студентов для прополки клубники в составе начальника и подчиненных?

Речь идет о выборе упорядоченных двухэлементных подмножеств множества студентов, состоящего из трех элементов (К = {1, 2, 3}), т. е. о размещениях без повторений из трех элементов по 2, поэтому:

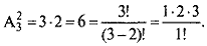
Подробнее в виде векторов из номеров студентов (например, по журнальному списку) первая компонента которого обозначает номер студента-начальника, вторая — подчиненного:

(1,2), (1,3), (2,1), (2,3), (3,1), (3,2).

Ясно, что здесь существенен порядок следования компонентов и не может быть повторений (один студент не может быть начальником и подчиненным одновременно), поэтому это множество — подмножество декартового произведения.

Перестановки

Рассмотрим различные упорядочения n -элементного множества X (вектора длины n , составленные из n -элементного множества). В отличие от декартова произведения полученные при этом векторы отличаются лишь порядком следования элементов и называются перестановками без повторений из п элементов . Число перестановок без повторений из n элементов обозначается Р n. К перестановкам без повторений можно прийти, полагая, что осуществляется размещение без повторений из n элементов по n :

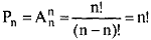
Считается, что 0! = 1.

Пример.Сколько существует возможных последовательностей выполнения проверок финансовой деятельности трех подразделений?

Требуется получить число перестановок без повторений из трех элементов, т. е. Р3= 3! = 6.

Получим все эти последовательности:

(1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,1,2), (3,2,1).

Пример.Сколько можно составить пятизначных шифров-чисел, не кратных 5, из цифр 1, 2, 3, 4, 5 без повторений цифр?

Всего из пяти цифр можно составить Р5= 5! = 120 пятизначных шифров-чисел, но они будут включать и кратные 5. Сколько будет шифров, кратных 5? — Из данного набора чисел кратными 5 могут быть числа, содержащие 5 в младшем разряде. Если цифру 5 записать в младшем разряде, то остальные цифры 1, 2, 3, 4 можно распределить по разрядам Р4= 4! = 24 способами. Таким образом, число пятизначных шифров из чисел 1, 2, 3, 4, 5 без повторения чисел и не кратных 5 будет 120 – 24 = 96.

Перестановки без повторений можно интерпретировать как различные варианты векторов, состоящих из неповторяющихся компонентов, получаемые перестановкой компонентов.

По аналогии при наличии одинаковых компонентов в некотором векторе получаем задачу оценки так называемых перестановок с повторениями данного состава.

Рассмотрим вначале пример: сколько различных последовательностей-кодов можно получить, переставляя цифры в числе 010, т. е. векторов длины k = 3 из двухэлементного множества В = {0,1}, содержащих два нуля.

Имеется всего три разряда, которые обозначим р1, р2, р3. Их можно переставить р3= 3! = 6 способами. Запишем различные получаемые сочетания разрядов и соответствующие коды:

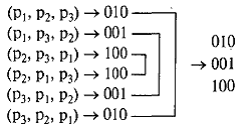
Видно, что коды повторяются тогда, когда несущественен порядок следования разрядов с одинаковой цифрой 0 (р1, р3). Все это соответствует тому факту, что имеются два способа (2!) перестановки этих разрядов ( pl, p 3), (р3, p 1) без изменения кода, т. е. неповторяющихся кодов будет меньше во столько раз, сколько имеется способов перестановки повторяющихся разрядов.

Рассмотрим более сложный случай.

Сколько различных «слов», не обязательно имеющих смысл, можно получить, переставляя буквы в слове «кишмиш»?

Здесь шесть букв слова можно переставить друг с другом р6= 6! = 720 способами, но в данном слове буквы «и» и «ш» повторяются дважды, и при их перестановке слова могут повторяться. Сколько же существует вариантов перестановок этих букв без изменения слова? Первый вариант — исходный, второй — поменять местами буквы «и», третий — поменять местами буквы «ш», четвертый — поменять местами как буквы «и», так и буквы «ш». Всего четыре варианта. С учетом того, что эти четыре варианта участвуют в порождении 720 способов, получим 720/4 = 180 различных «слов». Можно показать, что число раз, во сколько уменьшается количество слов по сравнению с числом перестановок без повторений, представляет собой произведение факториалов количества повторяющихся букв.

Таким образом, если из n элементов множества X = {х1, х2, ..., х n} составлен вектор V длины k , причем каждому i -му компоненту можно поставить в соответствие число ki, указывающее его число повторений в V , то задан вектор S = ( k 1, k 2, ..., kn), который называется составом данного вектора.

Так, для X = {0, 1, 2, 3} и V = (010223) состав: S = (2, 1, 2, 1).

Векторы одного и того же состава, отличающиеся лишь порядком компонентов, называются перестановками с повторениями данного состава.

Общая формула числа перестановок с повторениями данного состава имеет вид

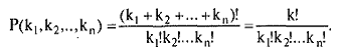
Пример.Сколько различных кодовых последовательностей можно получить перестановками кода 102202030?

Такому вектору, составленному из элементов множеств {0, 1, 2, 3}, соответствует вектор состава (1, 4, 3, 1), поэтому число различных кодовых комбинаций определяется как число перестановок с повторениями этого состава

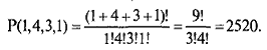
Сочетания

В ряде комбинаторных задач требуется определить число k -элементных подмножеств множества из n элементов. В этом случае порядок следования компонентов несущественен, т. е. производится неупорядоченная выборка. В результате получают так называемые сочетания без повторения.

Сочетаниями без повторений из п элементов по k называются отличающиеся друг от друга хотя бы одним элементом выборки длины k , составленные из n -элементного множества.

Число сочетаний без повторений из n элементов по k , обозначаемое как 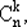определяется исходя из числа размещений без повторений с учетом того, что различных неупорядоченных векторов (подмножеств исходного множества) будет меньше в число раз, соответствующее числу перестановок без повторений из k элементов:

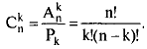
Пример.Определить число двухэлементных подмножеств множества, состоящего из трех элементов. Перечисляем все двухэлементные подмножества множества X = { х1, х2, х3}:

{х1, х2}, {х1, х3}, {х2, х3}.

Здесь мы имеем дело с сочетаниями из трех по 2:

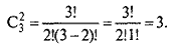
Это величина в 2! раза меньше, чем число размещений из 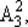поскольку компоненты двухэлементных векторов можно переставить Р2= 2! способами.

Пример.Сколькими способами можно выбрать 3 различных комбайна из 5 имеющихся?

Число размещений из пяти по 3 без повторений: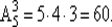

Один и тот же набор комбайнов можно получить различными способами, например, векторы (а, b , с) и ( b , а, с) дают один и тот же набор. Поскольку три элемента можно переставить Р3= 3! = 6 способами, то число способов выбора различных трех комбайнов равно

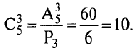
В ряде комбинаторных задач требуется подсчитывать число различных составов векторов длины k из n -элементного множества. Такие векторы-составы называются сочетаниями с повторениями из п элементов по k .

Например, требуется составить механизированные бригады из трех комплексов двух типов и определить количество таких бригад. Порядок следования комплексов в векторе бригады роли не играет, а каждая бригада задается вектором длины 3 из двух элементов, порядок компонентов которого роли не играет.

Получаем сочетания с повторениями из двух элементов по 3:

( m 1, m 1, m 1), ( m 1, m 2, m2), ( m 1, m 1, m 2), ( m 2, m2, m2),

где m означает тип комплекса.

Итак, можно построить бригаду из трех комплексов первого типа, трех комплексов второго типа, двух комплексов второго типа и одного первого и, наконец, двух комплексов первого типа и одного второго, т. е. четырьмя способами.

Определение числа сочетаний с повторениями можно произвести следующим образом.

Каждому сочетанию с повторениями из двух по 3 ставится в однозначное соответствие вектор длины n + k – 1 = 2 + 3 – 1 = 4, состоящий из трех нулей и n – 1 = 1 единицы (табл. 6).

Таблица 6