Определение числа сочетаний с повторениями

В таком случае число сочетаний с повторениями, которое обозначается равно числу перестановок с повторениями данного состава (вектор имеет одну единицу и три нуля), т. е.

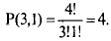
В общем случае это выражение имеет вид

что соответствует выражению

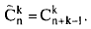
Например, требуется составить подразделения из 6 рабочих четырех специальностей и определить количество способов формирования таких подразделений.

Получаем сочетания с повторениями из четырех элементов по 6:

Бином Ньютона

Имеется формула, называемая биномом Ньютона, которая использует выражения числа сочетаний без повторений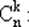

где a , b — действительные или комплексные числа.

Например:

Коэффициенты называются биномиальными . Докажем формулу бинома Ньютона по индукции. Доказательство по индукции предполагает:

1) базис индукции — доказательство того, что формула верна для конкретного n , например, для n = 1. В нашем случае мы убедились, что формула верна для n = 2, 3, 4. Убедимся, что она верна и для n = 1.

2) индукционный шаг. Предполагая, что формула верна для некоторого n , убеждаются, что тогда она верна и для n + 1;

3) при истинности шагов 1 и 2 заключают, что формула верна для любого n .

Приступим к индукционному шагу.

Возьмем выражение и получим из него выражение для n + 1. Очевидно, что это можно сделать путем умножения на (а + b ):

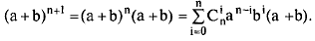
Преобразуем полученное выражение:

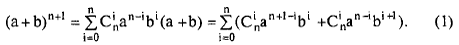
Для выполнения индукционного шага необходимо показать, что это выражение равно выражению

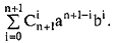
Рассмотрим подвыражение выражения (1): 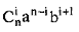и заменим i на i – 1.

Получим 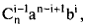т. е. одинаковые коэффициенты 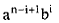перед выражениями для числа сочетаний в первом и втором подвыражении выражения (1).

Это позволит вынести an – i + lbiза скобку. Но в не учтен n -й член подвыражения 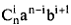(суммирование идет до n ): тогда, учитывая его, получаем:

Нетрудно видеть, что 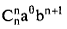можно заменить на 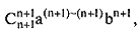кроме того, мы уже доказали, что поэтому: 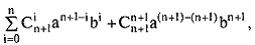что, очевидно, равно выражению

По индукции получаем, что формула бинома Ньютона верна для любого n .