Множества и основные операции над ними

Основные понятия теории множеств

Понятия множества и элемента множества относятся к понятиям, не определимым явно, таким, как, например, точка и прямая. Это связано с тем, что некоторые понятия в математике должны быть исходными, служить теми «кирпичиками», из которых складывается общая теория. Мы определяем только, как соотносятся эти исходные понятия, не говоря о природе рассматриваемых объектов.

Под множеством М понимается совокупность некоторых объектов, которые будут называться элементами множества М . Тот факт, что х является элементом множества М , будем обозначать через х Î М (читается « x принадлежит М »), а если х не является элементом множества M , то будем писать х Ï М (читается « x не принадлежит М »).

Заметим, что элементы множества сами могут являться множествами. Например, множество групп студентов состоит из элементов (групп), которые, в свою очередь, состоят из студентов.

Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы множества должны удовлетворять. Если x 1, x 2, …, xn— все элементы множества М , то будем писать М = { x 1, x 2, …, xn}. Пусть имеется свойство Р , которым могут обладать или не обладать элементы некоторого множества А . Тогда множество М , состоящее из всех элементов множества А , обладающих свойством Р , будет обозначаться через {х Î А | х обладает свойством Р }, а также {х | х обладает свойством Р }, {х | Р {х )} или { x } P(x), когда из контекста ясно, о каком множестве А идет речь.

Мы будем использовать следующие обозначения для числовых множеств: ℕ или ω — множество натуральных чисел, ℤ — множество целых чисел, ℚ — множество рациональных чисел, ℝ — множество вещественных чисел, ℂ — множество комплексных чисел.

Пример 1.1. Множество М арабских цифр можно задать двояко: перечислением М= {0, 1, 2, …, 9} или посредством свойства М = {х | х — арабская цифра}.

Пример 1.2. Множество нечетных чисел {±1, ±3, ±5, ...} можно определить как {х | х = 2k + 1 для некоторого k Î Z }.

Множество А называется подмножеством множества В (обозначается А Í В ), если все элементы множества А принадлежат В :

А Í В Û " x (x Î A Þ x Î B ).

Другими словами, это означает справедливость следующего утверждения: для любого элемента х , если x Î A , то x Î B . Если А Í В , то будем также говорить, что множество А содержится в В , или имеется включение множества А в В . Множества А и В называются равными или совпадающими , (обозначается А = В ), если (они состоят из одних и тех же элементов, т. е. если А Í В и В Í А . Таким образом, чтобы доказать равенство множеств, требуется остановить два включения.

Пример 1.3. Справедливы следующие включения: ℕ Í ℤ , ℤ Í ℚ , ℚ Í ℝ , ℝ Í ℂ .

Запись А Ì В или А ⊊ В означает, что А Í В и А ≠ В (А не равно B ), и в этом случае будем говорить, что А строго включено в В , или является собственным подмножеством В . Так, включения из примера 1.3 являются строгими.

Заметим, что X Í X ; если X Í Y и Y Í Z , то X Í Z ; если X Í Y и Y Í X , то X = Y .

Не следует смешивать отношение принадлежности Î и отношение включения Í . Хотя 0 Î {0} и {0} Î {{0}}, неверно, что 0 Î {{0}}, поскольку единственным элементом множества {{0}} является {0}.

Совокупность всех подмножеств множества А называется его булеаном или множеством-степенью и обозначается через Ƥ ( A ) или 2А. Таким образом, Ƥ ( A ) ⇌ {B | B ⊆ A }.

Мы будем предполагать, что существует множество, не содержащее ни одного элемента, которое называется пустым и обозначается через Æ . Ясно, что Ø ⊆ A для любого множества А .

Пример 1.5. Если А = {1, 2, 3}, то Ƥ ( A ) = {Æ , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, A }.

Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом и обозначается через U . Рассмотрим операции на булеане Ƥ ( U ) . Если А , В Î Ƥ ( U ) , то пересечение А Ç В и объединение A È B множеств А и В определяются равенствами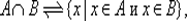

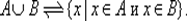
Пересечение множеств А и В называется также их произведением и обозначается А × В , а объединение — суммой : А + В . Множество 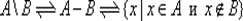называется разностью множеств А и В , множество 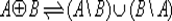— кольцевой суммой или симметрической разностью множеств А и В , множество 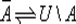— дополнением множества А в U {см. рис. 1.1, на котором изображены так называемые диаграммы Эйлера -Венна , наглядно поясняющие соотношения между множествами).

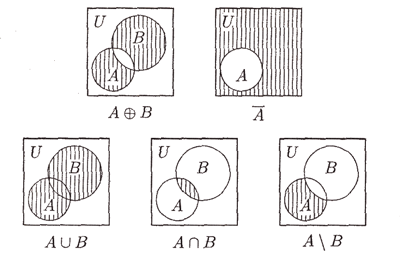
Рис. 1.1

Основные свойства операций пересечения, объединения и дополнения:

1. Ассоциативность операций ∪ и ∩ :

A ∪ (В ∪ С ) = (A ∪ В ) ∪ С , A ∩ (В ∩ С ) = (А ∩ В ) ∩ С .

2. Коммутативность операции ∪ и ∩ :

A ∪ В = В ∪ A , A ∩ В = В ∩ A .

3. Законы идемпотентности :

A ∪ A = A , A ∩ A = A .

4. Законы дистрибутивности :

A ∪ (В ∩ С ) = (A ∪ В ) ∩ (A ∪ С ),

A ∩ (В ∪ С ) = (А ∩ В ) ∪ (A ∩ С ).

5. Законы поглощения :

A ∪ (A ∩ B ) = A , A ∩ (A ∪ B ) = A .

6. Законы де Моргана

.

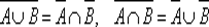7. Законы нуля и единицы : положим 0 ⇌ ∅ , 1 ⇌ U , тогда

A ∪ 0 = A , A ∩ 0 = 0, A ∪ 1 = 1, A ∩ 1 = A ,

.

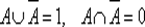8. Закон двойного отрицания

.

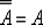Отметим, что операция выражается через операции ∩ и ¯. По закону де Моргана и закону двойного отрицания справедливо соотношение 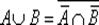, т. е. операция ∪ также выражается через операции ∩ и ¯. По определению операция ⊕ тоже выражается через ∩ и ¯. Таким образом, любая из определенных операций над множествами выражается через операции ∩ и ¯.

Пересечение и объединение могут быть определены для любого множества множеств Ai, где индексы i пробегают множество I . Пересечение ∩ {Ai| i ∈ I } и объединение ∪ {Ai| i ∈ I } задаются равенствами

∩ {Ai| i ∈ I } ⇌ {x | x ∈ Aiдля всех i ∈ I },

∪ {Ai| i ∈ I } ⇌ {x | x ∈ Aiдля некоторого i ∈ I }.

Вместо ∩ {Ai| i ∈ I } и ∪ {Ai| i ∈ I } часто пишут соответственно 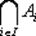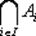, а иногда просто, ∩ Ai, ∪ Aiесли из контекста, ясно, какое множество I имеется в виду. Если I = {1, 2, …, n }, то используются записи

A 1∩ A 2∩ … ∩ Anи A 1∪ A 2∪ … ∪ An, а также 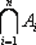и .

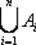Множество {Ai| i ∈ I } непустых подмножеств множества А называется покрытием множества А , если 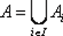. Покрытие называется разбиением , если Ai∩ Aj∅ при i = j . Другими словами, множество {Ai| i ∈ I } непустых подмножеств множества A является его разбиением, если каждый элемент х ∈ А принадлежит в точности одному из подмножеств А i, каждое из которых не является пустым.

Предложение 1.1.Следующие условия эквивалентны :

1) А ⊆ В ; 2) А ∩ В = А ; 3) А ∪ В = В ; 4) A В = 0; 5) .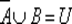

Доказательство. 1 ⇒ 2. Так как А ∩ В ⊆ А , то достаточно показать, что А ⊆ В влечет А ⊆ A ∩ В . Но если x ∈ A , то по условию x ∈ B , и, следовательно, x ∈ А ∩ В .

2 ⇒ 3. Так как А ∩ В = A , то A ∪ B = (A ∩ B ) ∪ B ). По закону поглощения и закону коммутативности имеем (A ∩ B ) ∪ B ) = B . Тогда А ∪ В = В .

3 ⇒ 4. Предположим, что А ∪ В = В . Так как 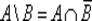, то по закону де Моргана, закону ассоциативности, закону коммутативности и законам нуля и единицы имеем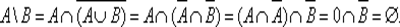

4 ⇒ 5. Предположим, что А В = ∅ , т. е. 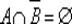. Тогда 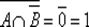. По закону де Моргана и закону двойного отрицания получаем .

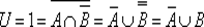5 ⇒ 1. Предположим, что 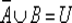и не выполняется условие А ⊆ В , т. е. найдется элемент x такой, что x ∈ A и x ∉ B . Тогда 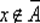и, значит, 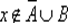, а это противоречит равенству .

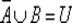Упорядоченную последовательность из n элементов x 1, x 2, …, xnбудем обозначать через (x 1, x 2, …, xn) или á x 1, x 2, …, xnñ . Здесь круглые или угловые скобки используются для того, чтобы указать на порядок, в котором записаны элементы. Будем называть такую последовательность упорядоченным набором длины п , кортежем длины п или просто п -кой. Элемент xiназывается i - й координатой кортежа á x 1, x 2, …, xnñ . В теории множеств кортежи кодируются с помощью операции взятия множества по двум элементам в соответствии со следующими правилами:

áñ ⇌ ∅, á x 1ñ ⇌ x 1, á x 1, x 2ñ ⇌ {{x 1}, {x 1, x 2}}, á x 1, x 2, …, xn+ 1ñ ⇌ áá x 1, x 2, …, xnñ , xn+ 1ñ .

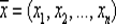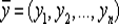Заметим, что две n -ки и равны 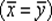тогда и только тогда, когда x 1= y 1, x 2= y 2, …, xn= yn.

Пример 1.5.Пары (1, 2) и (2, 1) не совпадают, хотя множества {1, 2} и {2, 1} равны.

Декартовым (прямым ) произведением множеств A 1, A 2, …, Апназывается множество {(x 1, x 2, …, xn) | x 1∈ A 1, x 2∈ A 2, …, xn∈ An}, обозначаемое через A 1× A 2× … × Апили 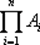. Если A 1= A 2= … = Ап= A то множество A 1× A 2× … × Апназывается n -й декартовой степенью множества А и обозначается An. Положим по определению A 0⇌ {∅ }.

Пример 1.6. Пусть А = {1, 2}, В = {3, 4}. Тогда А × В = {(1, 3), (1, 4), (2, 3), (2, 4)}, В × А = {(3, 1), (3, 2), (4, 1), (4, 2)}, А × A = {(1, 1), (1, 2), (2, 1), (2, 2)}.

Пример 1.7. (шахматная доска). Рассмотрим два множества А = {a , b , c , d , e , f , g , h } и B = {1, 2, 3, 4, 5, 6, 7, 8}. Тогда множеству пар (x , y ) ∈ А × В соответствует множество клеток шахматной доски.

Пример 1.8. Множество [0, 1]2равно множеству {(а , b ) | 0 ≤ a ≤ 1, 0 ≤ b ≤ 1}, которому соответствует множество точек на плоскости, имеющих неотрицательные координаты, не превосходящие единицы (рис. 1.2).

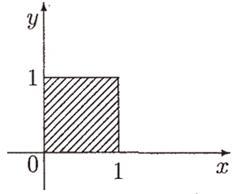
Рис. 1.2

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов , Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ , 2003. — С. 10–16. — (Серия «Высшее образование»).