Кортеж. Декартово произведение

Пусть А и В — произвольные множества. Неупорядоченная пара на множествах А и В — это любое множество {а , b }, где а ∈ А , b ∈ В или a ∈ B , b ∈ A .

Если А = В , то говорят о неупорядоченной паре на множестве А . Исходя из понятия равенства множеств , можно утверждать, что неупорядоченная пара {а , b } равна неупорядоченной паре {с , d } если и только если а = с и b = d или а = d и b = с . Заметим, что равенство элементов множества понимается здесь (и далее в аналогичных ситуациях) как равенство индивидных констант.

В том случае, когда в неупорядоченной паре {а , b } элементы а и b совпадают, получаем, что {а , b } = {а , a }. Но такая запись, как мы условились выше, задает то же самое множество, что и { a }. Таким образом, при а = b неупорядоченная пара {а , b } «вырождается» в одноэлементное множество {а }. При а ≠ b неупорядоченная пара будет двухэлементным множеством.

Упорядоченная пара на множествах А и В , обозначаемая записью ( a , b ), определяется не только самими элементами а ∈ А и b ∈ В , но и порядком, в котором они записаны. И в этом состоит ее существенное отличие от неупорядоченной пары. Если А = В , то говорят об упорядоченной паре на множестве А.

Существенная роль порядка, в котором перечисляются элементы упорядоченной пары, фиксируется определением равенства упорядоченных пар.

Определение 1.1.Две упорядоченные пары (а , b ) и (а ', b ') на множествах А и В называют равными, если а = a ' и b = b '.

Замечание 1.2.Упорядоченную пару (а , b ) не следует связывать с множеством {а , b }, так как упорядоченная пара характеризуется не только составом, но и порядком элементов в ней. Более того, определение этого объекта вообще не позволяет рассматривать его как множество. Но упорядоченную пару можно определить и как множество, полагая, что упорядоченная пара (а , b ) есть неупорядоченная пара {{ a }){а , b }}, включающая в себя одноэлементное множество {а } и неупорядоченную пару {а , b }. При a = b получаем (а , а ) = {{а }}. Такое определение не изменит сути понятия, но тогда следует не определять явно равенство упорядоченных пар, а доказывать теорему о равенстве упорядоченных пар как определенного вида множеств.

Простейший и важнейший пример использования упорядоченных пар дает аналитическая геометрия.Если на плоскости введена некоторая прямоугольная система координат , то каждая точка плоскости однозначно задается упорядоченной парой действительных чисел — координатами этой точки. Ни у кого не возникает сомнений в том, что порядок, в котором перечисляются координаты точки, является существенным: точка, заданная координатами (1, 3), совсем не то же самое, что точка с координатами (3, 1).

Обобщением понятия упорядоченной пары является упорядоченный п-набор, или кортеж. В отличие от конечного множества { a 1, .., an} кортеж ( a 1, ..., an) на множествах A 1, ..., Апхарактеризуется не только входящими в него элементами a 1∈ А 1, ..., ап∈ Ап, но и порядком, в котором они перечисляются. Как и для упорядоченных пар, роль порядка в кортеже фиксируется определением равенства кортежей.

Определение 1.2.Два кортежа ( a 1, ..., an) и ( b 1, ..., bn) на множествах A 1, ..., Ап равны, если

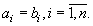
Число n называется длиной кортежа (или размерностью кортежа), а элемент ai— i -й проекцией(компонентой) кортежа. Для двух кортежей одинаковой размерности их компоненты с одинаковыми номерами называют одноименными компонентами. Определение 1.2 равенства кортежей можно переформулировать так: два кортежа одинаковой размерности равны тогда и только тогда, когда их одноименные компоненты совпадают.

Простейшим примером кортежа является арифметический вектор.

Определение 1.3.Множество всех кортежей длины п на множествах A 1, ..., Апназывают декартовым (прямым) произведением множеств A 1, ..., Апи обозначают A 1× ... ×Ап.

Таким образом,

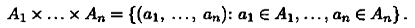
Если все множества 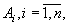равны между собой, то указанное декартово произведение называют n -й декартовой степенью множества А и обозначают Ап. В частности, при п = 2 получаем декартов квадрат, а при п = 3 — декартов куб множества А.

По определению полагают, что первая декартова степень любого множества А есть само множество A , т. е. А 1= А. Декартово произведение имеет следующие свойства:

1) А × ( B ∪ C ) = (А × В ) ∪ (А × С );

2) А × (В ∩ С ) = (А × В ) ∩ (А × С );

3) А × ∅ = ∅ × А = ∅.

Обратим внимание на последнее из записанных выше трех тождеств. Из него вытекает, что пустое множество при построении декартовых произведений множеств играет ту же роль, что и нуль при умножении чисел. Докажем справедливость этого тождества. В самом деле, множество ∅ × А (для любого A ) есть множество всех упорядоченных пар ( x , y ), таких, что х ∈ ∅ и y ∈ А. Но таких элементов х , что х ∈ ∅ , не существует, и, следовательно, упорядоченных пар ( x , y ), принадлежащих декартову произведению ∅ × А , не существует, т. е. ∅ × А = ∅ . Аналогично доказывается, что и А × ∅ = ∅ .

Мощность множества

Множество А равномощно множеству В , если существует биекция f : A → В.

Из того, что существует биекция f : A → В , следует, что соответствие f –1есть биекция B на А . Поэтому если А равномощно В , тон В равномощно А, и мы можем говорить, что множества Ал В равномощны.

Факт равномощности множеств А и В будем записывать так: А ~ В.

Из определения равномощности и свойств биекции также следует, что для любого множества А имеет место А ~ А (тождественное отображение есть биекция множества А на себя); а для любых множеств А , В , С из А ~ В и В ~ С следует А ~ С (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть отношение эквивалентности* , заданное на «множестве всех множеств» (на самом деле на множестве всех подмножеств некоторого универсального множества).

Если мы обозначим через |А | класс эквивалентности множества А по отношению ~, то утверждение о равномощности множеств Аи В можно записать так: |А | = | B |.

Этот класс эквивалентности |А | называют мощностью множества А.

Конечные множества А = { a 1, ..., an} и В = { b 1, ..., bm} равномощны тогда и только тогда, когда множества А и В состоят из одного и того же числа элементов, т. е. п = т. Отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству. Это свойство конечных множеств можно сформулировать так.

Теорема 1.8.Если А — конечное множество и f : A → A — инъекция, то она является сюръекцией и, следовательно, биекцией.

В силу приведенных выше соображений мощностью конечного множества А = { a 1, ..., an} можно считать натуральное число п , так как, задавая такое число, мы задаем и класс всех (попарно равномощных) множеств вида { a 1, ..., an}. Обратно, каждый такой класс однозначно определяет натуральное число п как число элементов в каждом множестве данного класса. Естественно считается, что мощность пустого множества равна нулю.

Перейдем теперь к исследованию мощности бесконечных множеств. Таковы хорошо известные нам числовые множества ℕ , ℤ , ℚ , ℝ и ℝ .

Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают ℵ 0(читается «алеф нуль»).

Любую биекцию v : ℕ → М называют нумерацией счетного множества М ; если элемент М есть v ( n ) для некоторого п ∈ ℕ , то этот элемент М обозначаем через а nназывая натуральное число п номером элемента а nотносительно данной нумерации v .

Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности a 1, ..., an... или { an}п ∈ ℕ . Другими словами, счетное множество есть область значений некоторой функции натурального аргумента.

Рассмотрим свойства счетных множеств.

Свойство 1 .Любое бесконечное множество содержит счетное подмножество.

Свойство 2 .В любом бесконечном множестве можно выделить два не пересекающихся между собой счетных подмножества.

Свойство 3 .Любое подмножество счетного множества конечно или счетно.

Если множество конечно или счетно, его называют не более чем счетным. Семейство (А i) i ∈ Iмножеств называют не более чем счетным, если множество (индексов) / не более чем счетно.

Свойство 4 .Объединение любого не более чем счетного семейства счетных множеств счетно.

Свойство 5 .Объединение конечного и счетного множеств счетно.

Свойство 6 .Пусть М — бесконечное множество, a N — его не более чем счетное подмножество. Если множество M N бесконечно, то оно равномощно множеству М.

Следствие .Если М — бесконечное множество, а N — не более чем счетное множество, то М ~ М ∪ N.

Существуют бесконечные множества, не являющиеся счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и единиц, т. е. последовательностей вида { α 1, α 1, ..., αn,…}, где αi∈ {0,1} для каждого i ≥ 1.

Обозначим множество таких «двоичных» последовательностей через {0,1}ω.

Свойство 7 . (теорема Кантора). Множество {0,1}ωне есть счетное множество.

Свойство 8 . Множество 2 ℕ всех подмножеств множества натуральных чисел и множество {0,1}ωравномощны.

Следующие множества равномощны:

1) множество действительных чисел отрезка [0,1];

2) множество действительных чисел интервала (0,1);

3) множество действительных чисел отрезка [ a , b ];

4) множество действительных чисел интервала ( a , b );

5) множество действительных чисел (числовая ось) ℝ ;

6) множество всех подмножеств множества натуральных чисел 2 ℕ .

Покажем равномощность множеств [0,1] и (0,1). Из множества действительных чисел отрезка [0,1] выделим двухэлементное подмножество {0,1}. Разностью этих множеств будет множество действительных чисел интервала (0,1), и, согласно свойству 6, [0,1] ~ (0,1).

Отображение у = ( b – а )х + а задает биекцию множества [0,1] на множество [а , b ]. Следовательно, эти множества равномощны. Заметим, что аналогично доказывается равномощность (0,1) и (а , b ).

Покажем, что (0,1) ~ ℝ . Биекцию можно установить, например, с помощью функции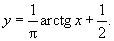

Поскольку равномощность [0,1] и 2 ранее доказана, имеем [0,1] ~ (0,1) ~ [а , b ] ~ (а , b ) ~ ℝ ~ 2 ℕ .

До сих пор речь шла о равенстве мощностей. Однако мощности разных множеств можно в определенном смысле сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества А не превышает мощность множества В (|А | ≤ | B |), если А равномощно некоторому подмножеству множества В. Можно показать, что из соотношений |А | ≤ |В | и |В | ≤ |А | следует, что |А | = | B |.

Мощность множества А считается строго меньшей мощности множества В (|А | < |В |), если множества А и В неравномощны и существует собственное подмножество С множества В , равномощное множеству А , т. е.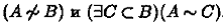

Можно доказать, что из |А | ≤ |В | и | B | ≤ | C | следует |А | ≤ | C |. Таким образом, на множестве всех мощностей (т. е. на множестве всех классов эквивалентности по отношению ~) установлено отношение порядка.

Из определения сразу следует, что мощность любого конечного множества строго меньше мощности ℵ 0, а из доказательства теоремы 1.15 вытекает, что ℵ 0< с. Кроме того, согласно теореме 1.9, мощность счетного множества ℵ 0является наименьшей на множестве всех бесконечных мощностей (т. е. мощностей бесконечных множеств). Можно сказать, что всякое бесконечное множество не менее чем счетно.

Без доказательства приведем важные теоремы.

Теорема 1.19 (теорема Кантора — Бернштейна). Для любых двух множеств А и В имеет место в точности одно из следующих трех условий: либо |А | < |В |, либо | B | < | A |, либо |А | = |В |.

Таким образом, любые два множества сравнимы по мощности. Другими словами, «шкала мощностей» линейно упорядочена.

Теорема 1.20.Для любого множества А верно неравенство |2А| > |А |.

В силу теоремы 1.20 нет наибольшей мощности, так как для любого множества А существует множество большей мощности — его булеан. Заметим, что для счетного множества А теорема 1.20 сводится к теореме Кантора.

Теорема 1,21 (теорема о квадрате). Для любого бесконечного множества М его декартов квадрат М × М равномощен самому множеству М.

В заключение приведем сводку результатов по мощностям некоторых конечных множеств.

Теорема 1.22.Если М и N — конечные множества и | M | = m , a | N |= n , то:

1) мощность множества всех отображений М в N равна nm;

2) мощность множества всех биекций из N на себя равна Рп= п !;

3) мощность множества всех инъекций из М в N ( m ≤ n )

4) мощность множества всех подмножеств множества N равна 2 n;

5) мощность множества всех k -элементных подмножеств множества N равна ;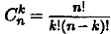

6) мощность прямого произведения М × N равна тп.

Напомним, что в комбинаторике число Рпназывают числом перестановок п элементов, число 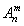— числом размещений без повторений из п элементов по т , число 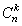(обозначаемое также 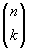) — числом сочетаний из п элементов по k . Эти числа называются также биномиальными коэффициентами , поскольку 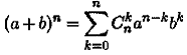(формула бинома Ньютона).

Цит. по: Дискретная математика: учебник для вузов /
А.И. Белоусов , С.Б. Ткачев; под ред. В.С. Зарубина , А.П. Крищенко. —
3-е изд. , стереотип. — М.: Изд-во МГТУ им. Баумана , 2004. — С. 37–40 , 89–100. —
(Сер. Математика в техническом университете; Вып. XIX).