Рекуррентные соотношения. Возвратные последовательности

Рекуррентным соотношением , рекуррентным уравнением , или рекуррентной формулой называется соотношение вида an + k = F ( n , an, an + 1 , …, an + k – 1 ), которое позволяет вычислять все члены последовательности a 0, a 1, a 2, …, если заданы ее первые k членов.

Пример 6.1.1. Формула an + 1 = an+ d задает арифметическую прогрессию.

2. Формула an + 1 = q · anопределяет геометрическую прогрессию.

3. Формула an + 2 = an + 1 + anзадает последовательность чисел Фибоначчи .

В случае, когда рекуррентное соотношение линейно и однородно, т. е. выполняется соотношение вида

an + k + p 1an + k – 1+ … + pkan = 0 (5.4)

( p = const ), последовательность a 0, a 1, a 2, … называется возвратной . Многочлен

Pa( x ) = xk+ p 1xk – 1 + … + pk (5.5)

называется характеристическим для возвратной последовательности { an}. Корни многочлена Pa( x ) называются характеристическими .

Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением .

Описание общего решения соотношения (5.4) имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами.

Теорема 6.1.1. Пусть λ — корень характеристического многочлена (5.5). Тогда последовательность { c λ n}, где с — произвольная константа, удовлетворяет соотношению (5.4).

2. Если λ 1, λ 2, …, λ k— простые корни характеристического многочлена (5.5), то общее решение рекуррентного соотношения (5.4) имеет вид ап= c 1λ 1n+ c 2λ 2n+ … + ckλ kn, где c 1, c 2, …, ck— произвольные константы.

3. Если λ j— корень кратности ri( i = 1, …, s ) характеристического многочлена (5.5), то общее решение рекуррентного соотношения (5.4) имеет вид 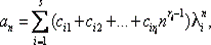где cij— произвольные константы.

Зная общее решение рекуррентного уравнения (5.4), по начальным условиям a 0, a 1, a 2, …, ak – 1 можно найти неопределенные постоянные cijи тем самым получить решение уравнения (5.4) с данными начальными условиями.

Пример 6.2.Найти последовательность {ап}, удовлетворяющую рекуррентному соотношению an + 2 – 4 an + 1 + 3 an= 0 и начальным условиям a 1= 10, a 2= 16.

Корнями характеристического многочлена Pa( x ) = x 2– 4 x + 3 являются числа x 1= 1 и x 2= 3. Следовательно, по теореме 6.1. общее решение имеет вид ап = c 1 + c 23 n. Используя начальные условия, получаем систему

решая которую, находим c 1= 7 и c 2= 1. Таким образом, а n= 7 + 3 n.

Рассмотрим неоднородное линейное рекуррентное уравнение

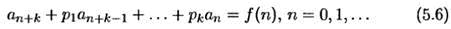
Пусть { bn} — общее решение однородного уравнения (5.4), а {сп} частное (конкретное) решение неоднородного уравнения (5.6). Тогда последовательность { b п+ сп} образует общее решение уравнения (5.6), и тем самым справедлива.

Теорема 6.2.Общее решение неоднородного линейного рекуррентного уравнения представляется в виде суммы общего решения соответствующего однородного линейного рекуррентного уравнения и некоторого частного решения неоднородного уравнения.

Таким образом, в силу теоремы 6.1. задача нахождения общего решения рекуррентного уравнения (5.6) сводится к нахождению некоторого частного решения.

В отдельных случаях имеются общие рецепты нахождения частного решения.

Если f ( n ) = β n (где β не является характеристическим корнем), то, подставляя ап= cβ пв (5.6), получаем с (β k+ p 1β k – 1 + … + p k) · β nи отсюда с · Ра( b ) = 1, т. е. частное решение можно задать формулой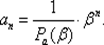

Пусть f ( n ) — многочлен степени k от переменной п , и число 1 не является характеристическим корнем. Тогда Ра(1) = 1 + p 1+ … + pk≠ 0 и частное решение следует искать в виде 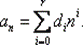Подставляя многочлены в формулу (5.6), получаем

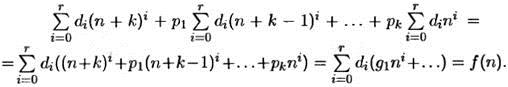
Сравнивая коэффициенты в левой и правой частях последнего равенства, получаем соотношения для чисел di, позволяющие эти числа определить.

Пример 6.3.Найти решение уравнения

an + 1 + 2ап= п + 1 (5.7)

с начальным условием а 0= 1.

Рассмотрим характеристический многочлен Ра(х ) = х + 2. Так как Р a(1) = 3 ≠ 0 и правая часть f ( n ) уравнения (5.6) равна n + 1, то частное решение будем искать в виде сп = d 0+ d 1· п . Подставляя спв уравнение (5.7), получаем ( d 0+ d 1(п + 1)) + 2( d 0+ d 1п ) = (3 d 0+ d 1)+ 3 d 1п = 1 + п . Приравнивая коэффициенты в левой и правой частях последнего равенства, получаем систему

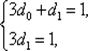
откуда, находим 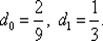Таким образом, частное решение уравнения (5.7) имеет вид 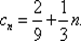По теореме 6.1. общее решение однородного уравнения an + 1 + 2ап= 0 задается формулой b п= с · (–2) n, и по теореме 6.2. получаем общее решение уравнения (5.7): 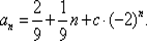Из начального условия а 0= 1 находим 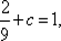, т. е. 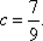Таким образом,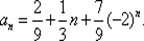

Цит. по: Элементы дискретной математики: учебник /
С.В. Судоплатов , Е.В. Овчинникова. — М.: ИНФРА-М;
Новосибирск: НГТУ , 2003. — С. 166–170 .— (Серия «Высшее образование»).