Вычисление спектра объединенной последовательности по спектрам расщепленных.
Пусть на периоде T имеем два сигнала 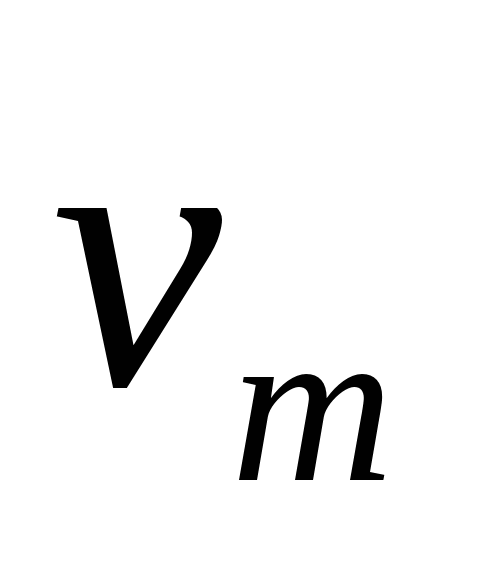 и
и 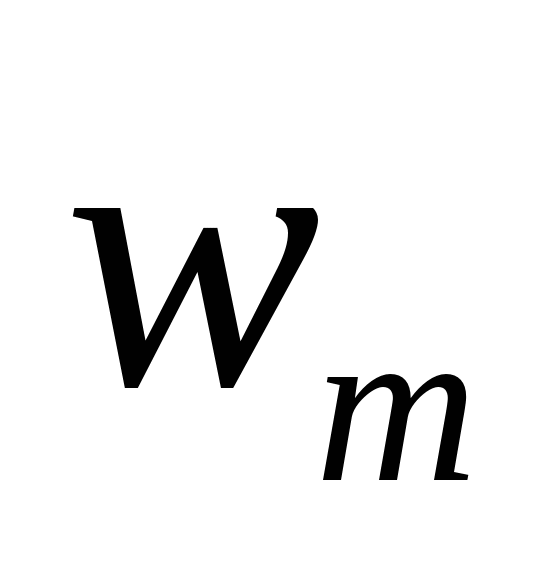 ,
, 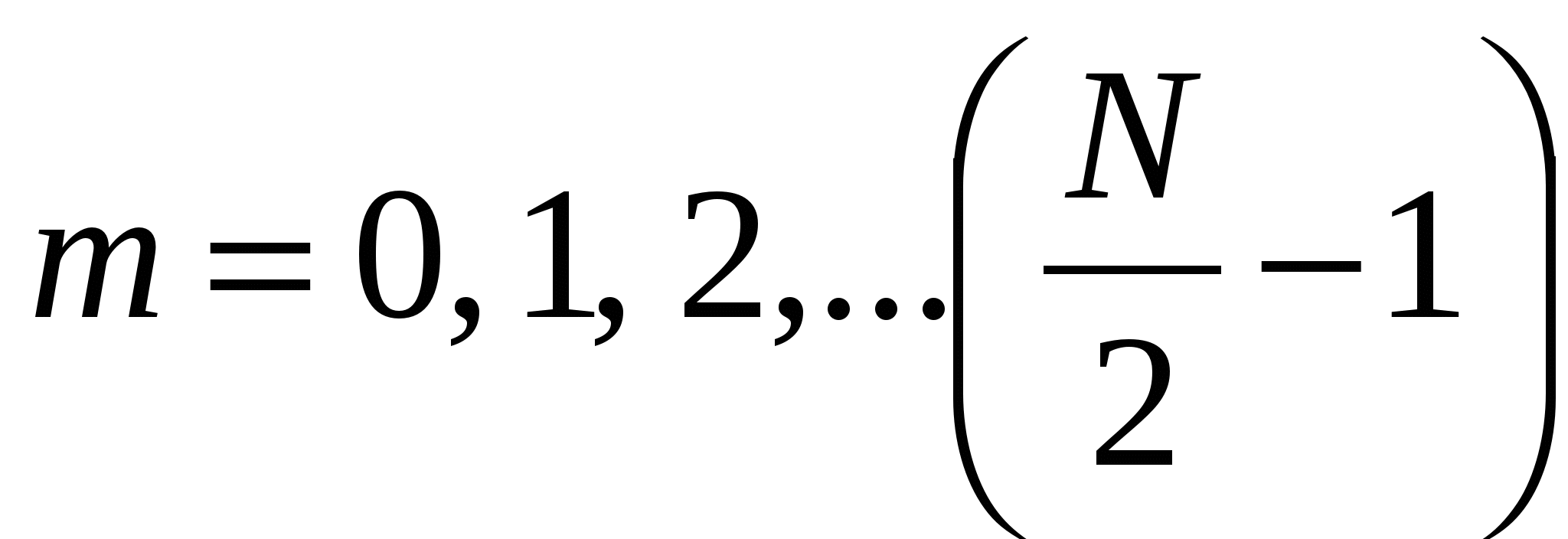 , каждый из которых содержит N/2 точек и имеет безразмерный шаг дискретизации
, каждый из которых содержит N/2 точек и имеет безразмерный шаг дискретизации 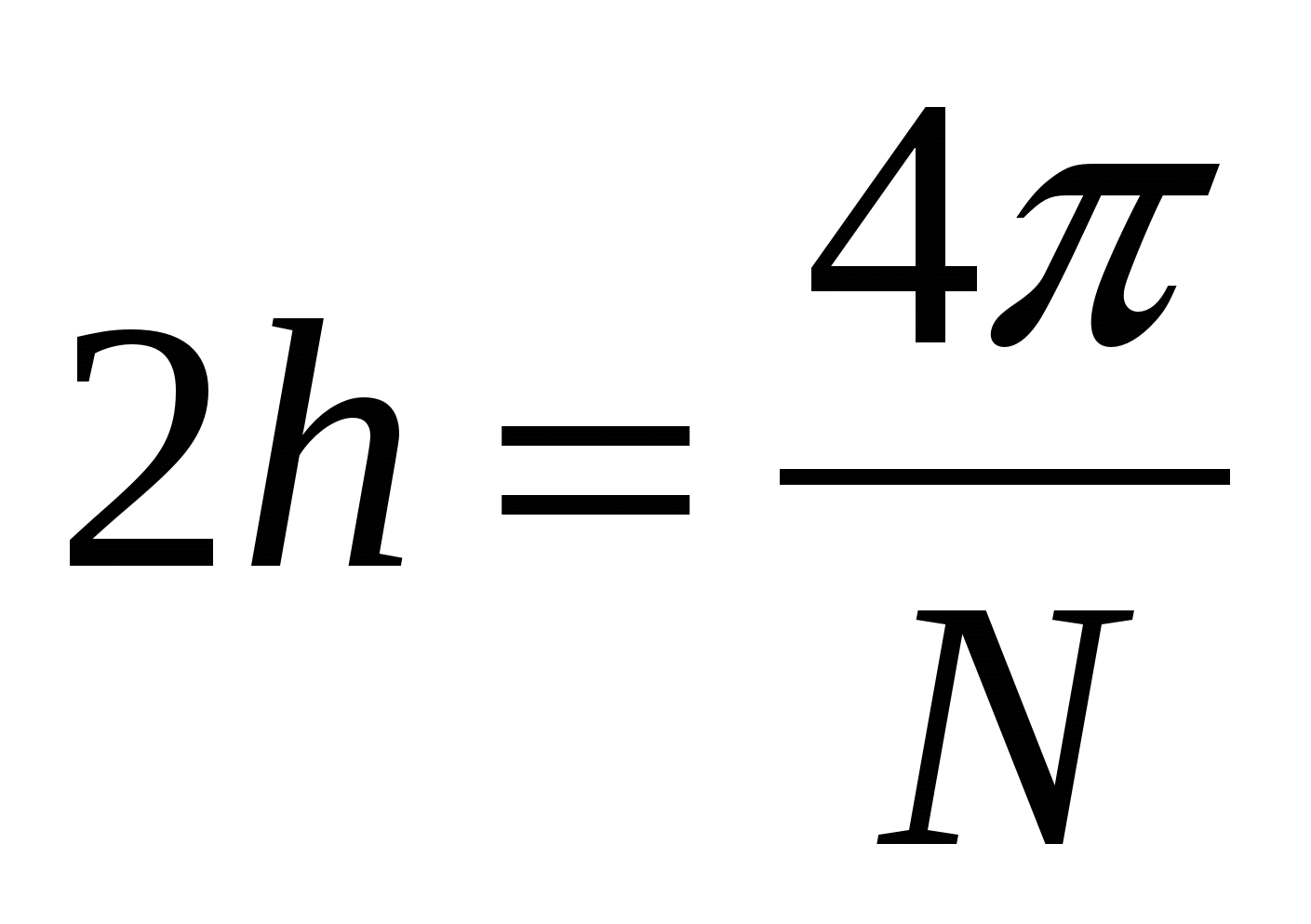 . Из этих двух сигналов, объединяя их в виде “гребенки”, получаем объединенную последовательность
. Из этих двух сигналов, объединяя их в виде “гребенки”, получаем объединенную последовательность 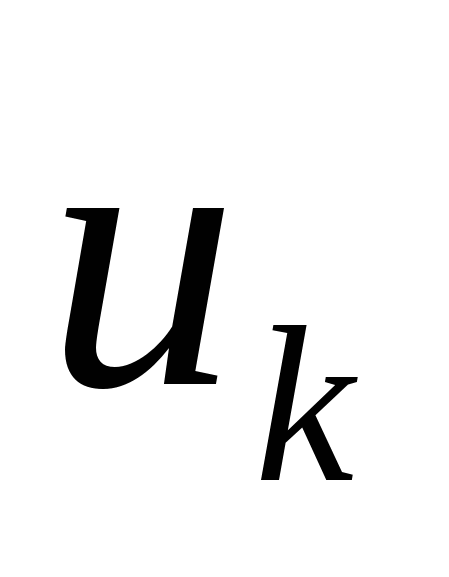 ,
, 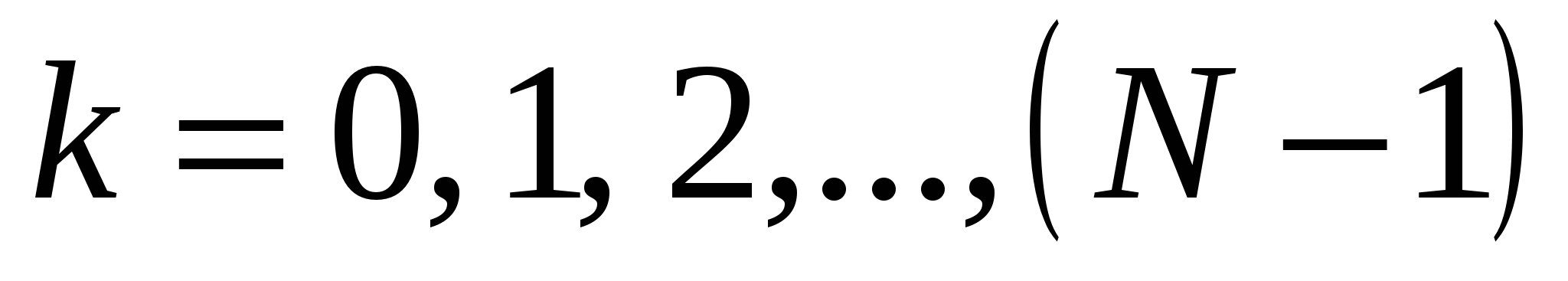 , состоящую из
, состоящую из  отсчетов. При таком объединении для четных
отсчетов. При таком объединении для четных 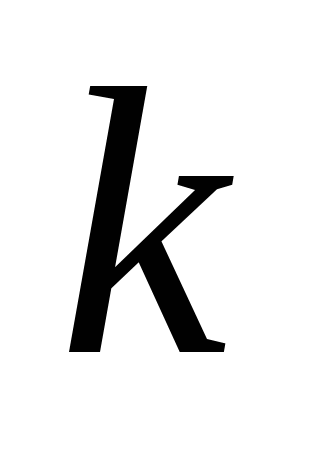 при
при 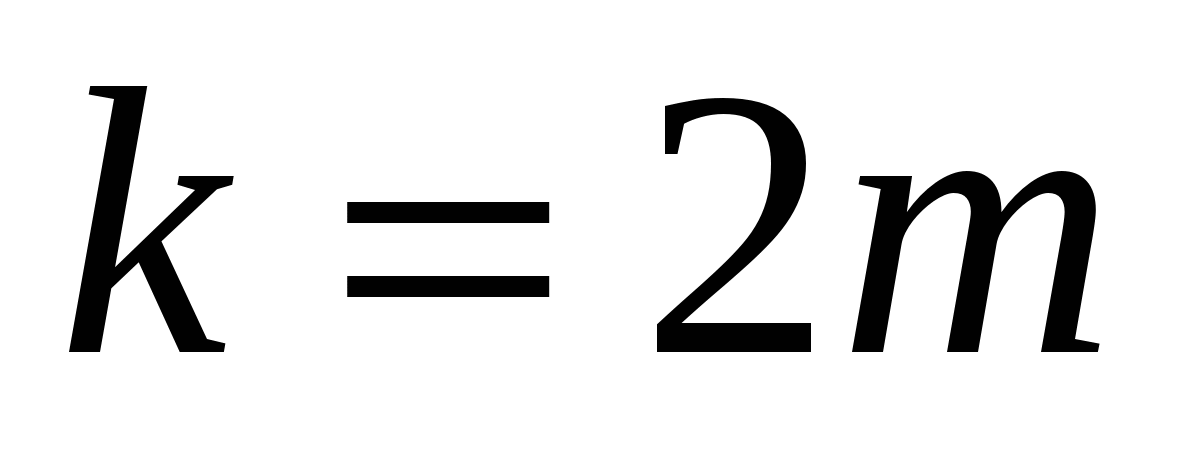 имеем
имеем 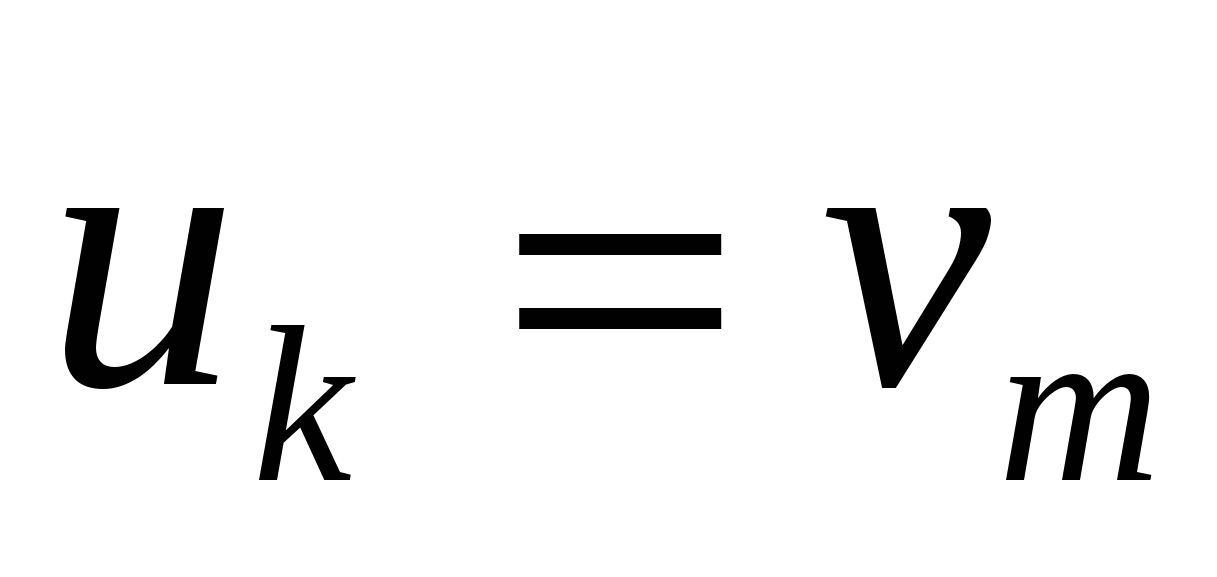 , для нечетных
, для нечетных 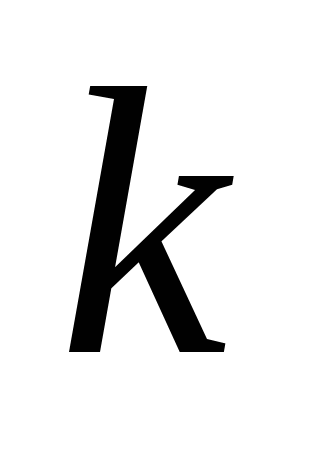 при
при 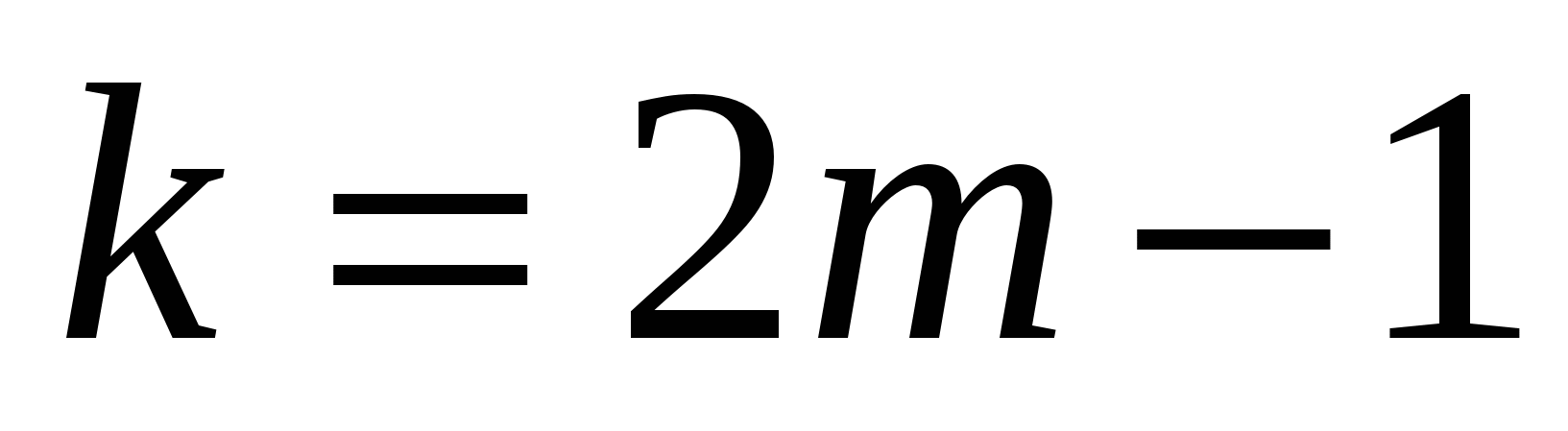 имеем
имеем 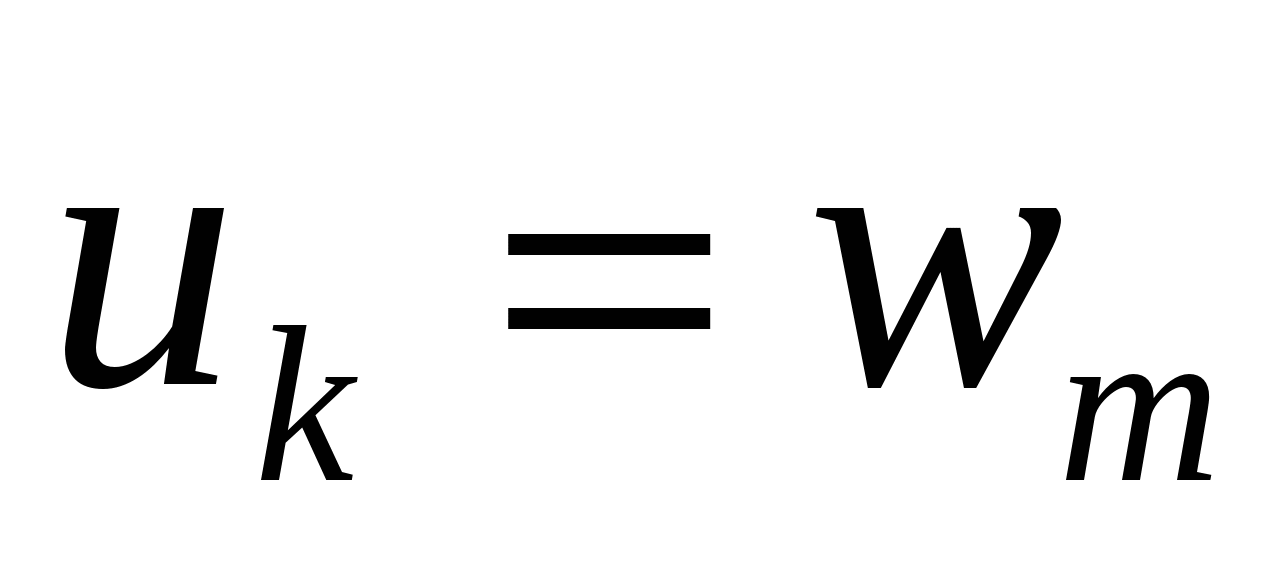 . Например,
. Например, 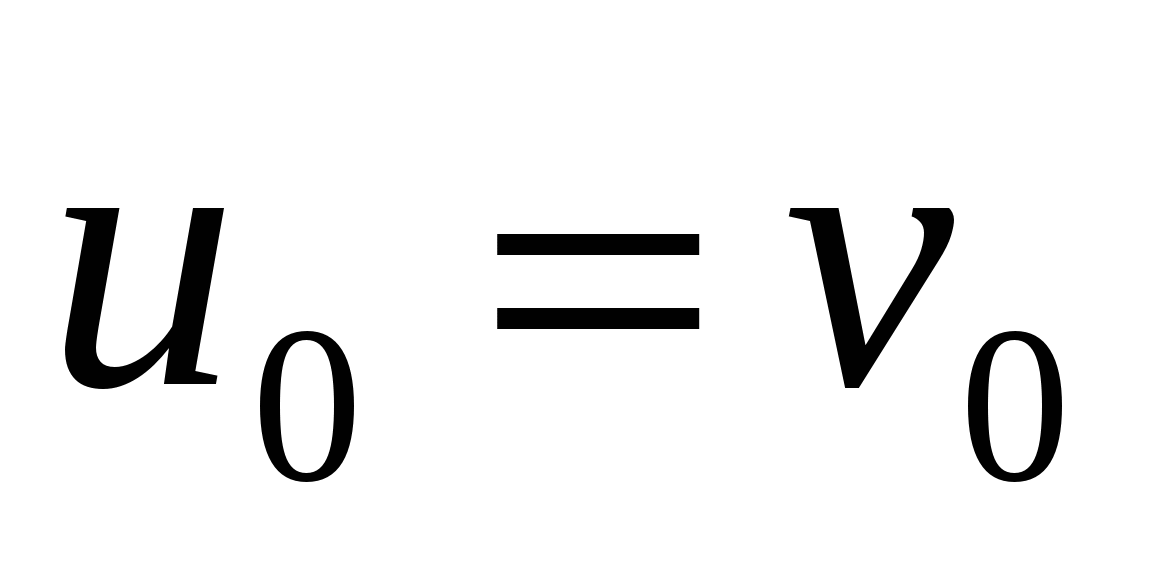 ,
, 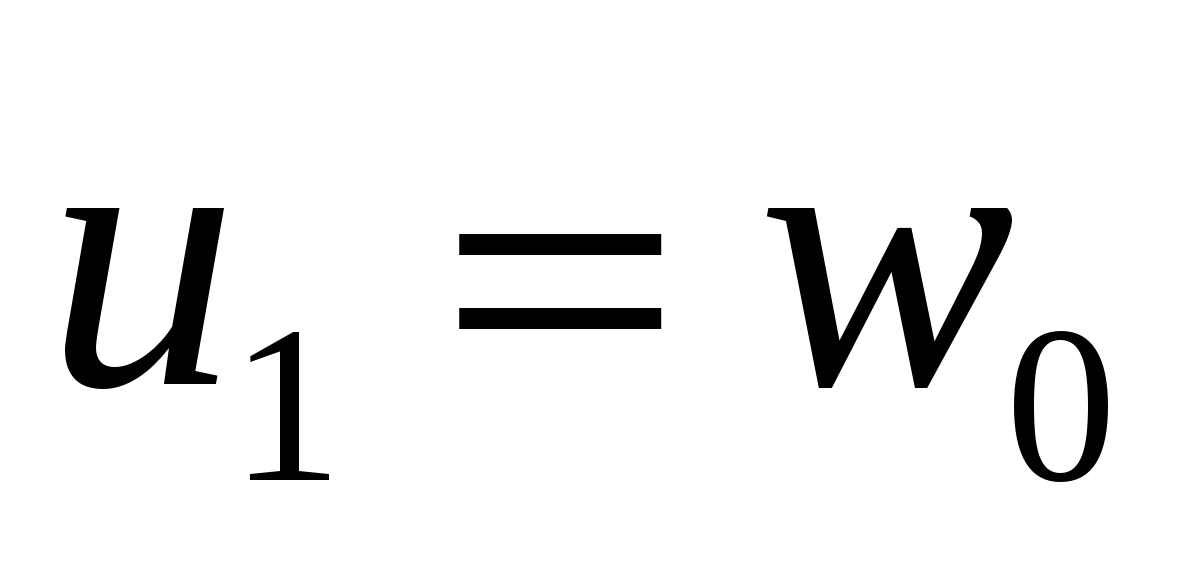 ,
, 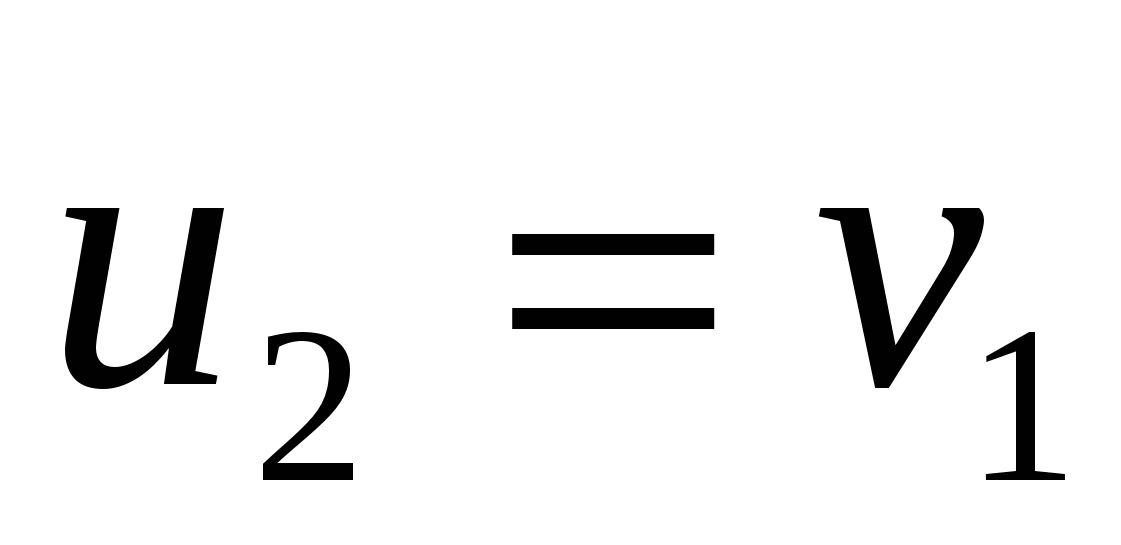 ,
, 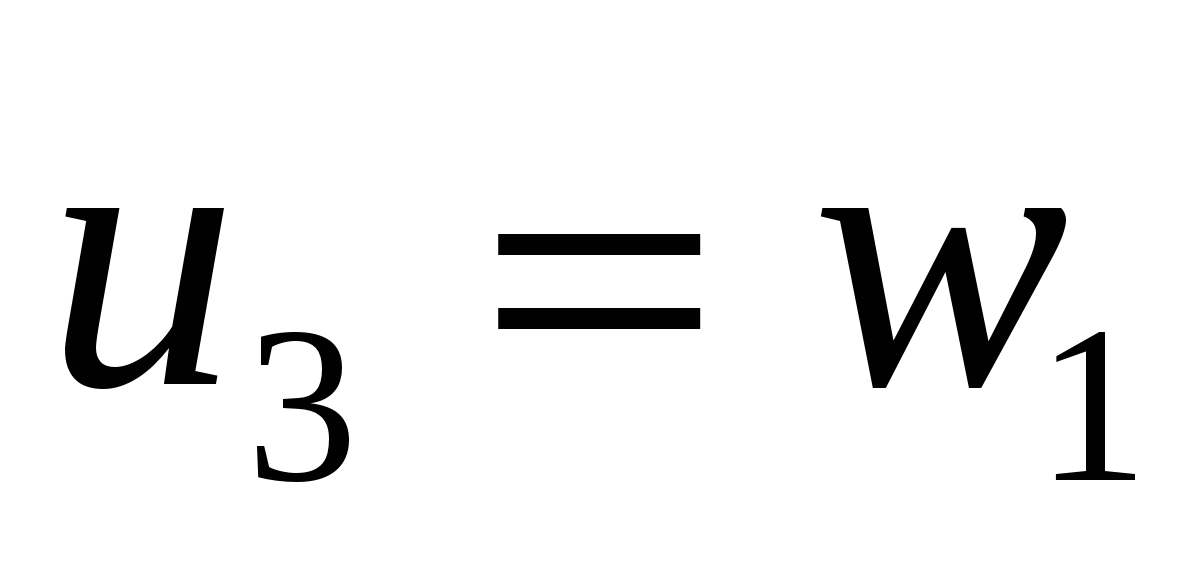 и т.д. Для объединенного сигнала получается шаг
и т.д. Для объединенного сигнала получается шаг 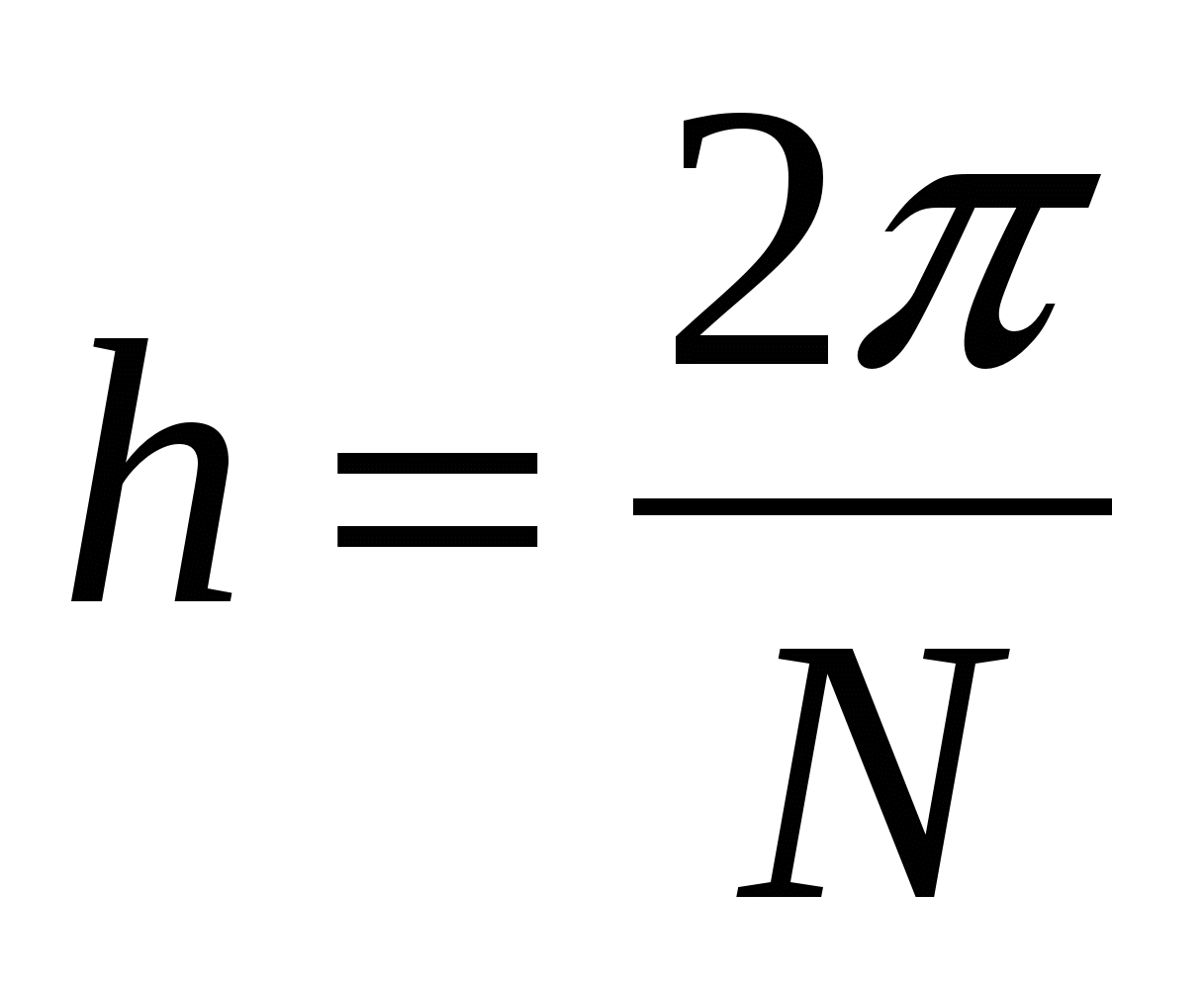 .
.
Рассматриваемые сигналы даны на рисунке 2.6

|
| Рис. 2.6 Две расщепленных и объединенная последовательности отсчетов. |
Запишем спектры этих трех сигналов в комплексной форме (14.7), причем для спектров будем использовать заглавные буквы, соответственно строчные - для сигналов.
ДПФ для исходного сигнала (15.3) требует  опреаций в строке (
опреаций в строке ( 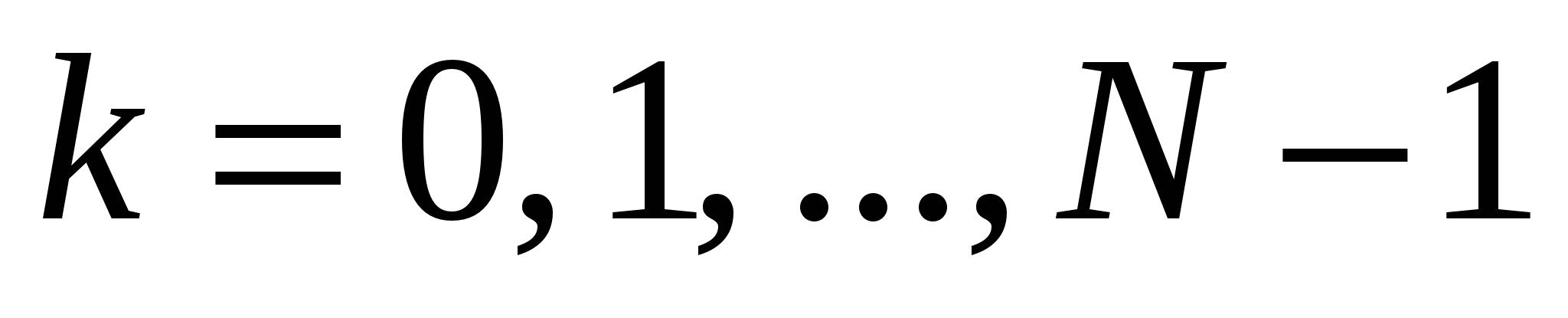 ) (операция – это вычисление константы, умноженное на
) (операция – это вычисление константы, умноженное на 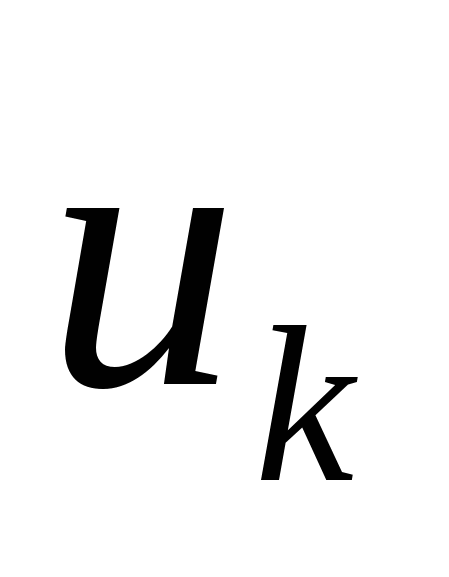 , прибавление к предыдущему), всего
, прибавление к предыдущему), всего 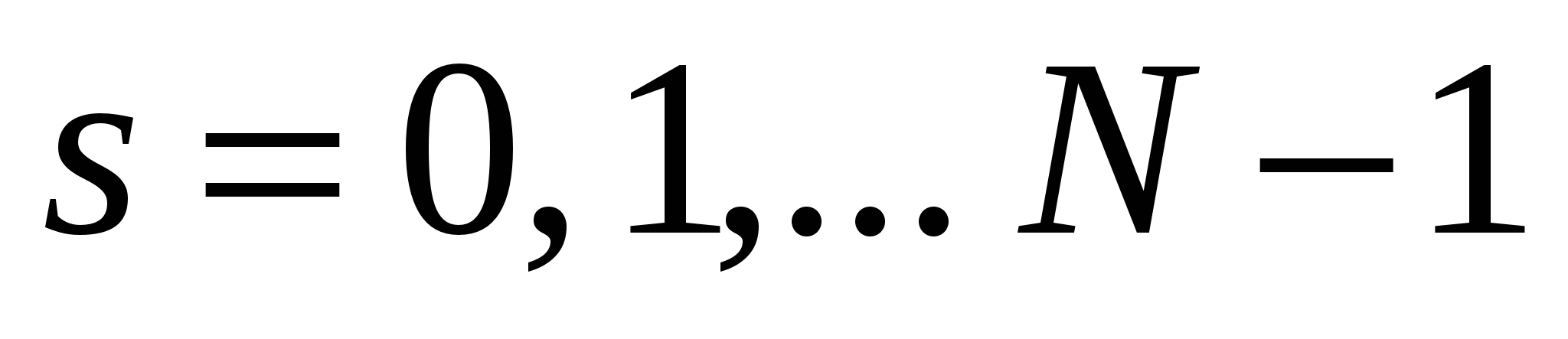 , т.е.
, т.е.  строк, операций
строк, операций 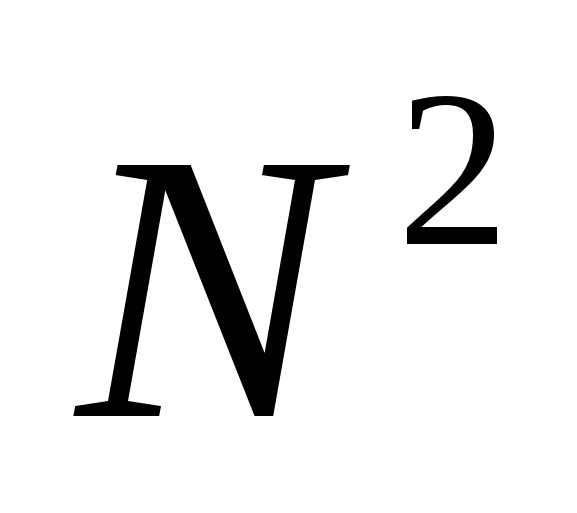 .
.
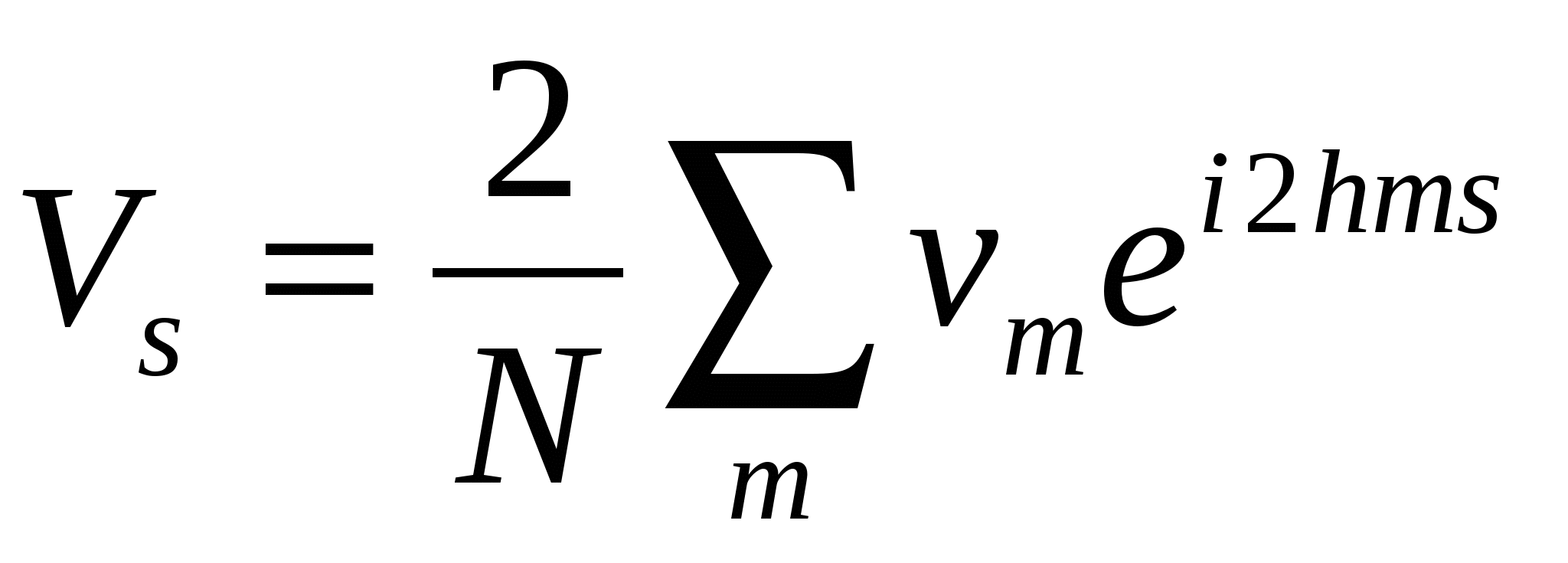
| (2.33) |
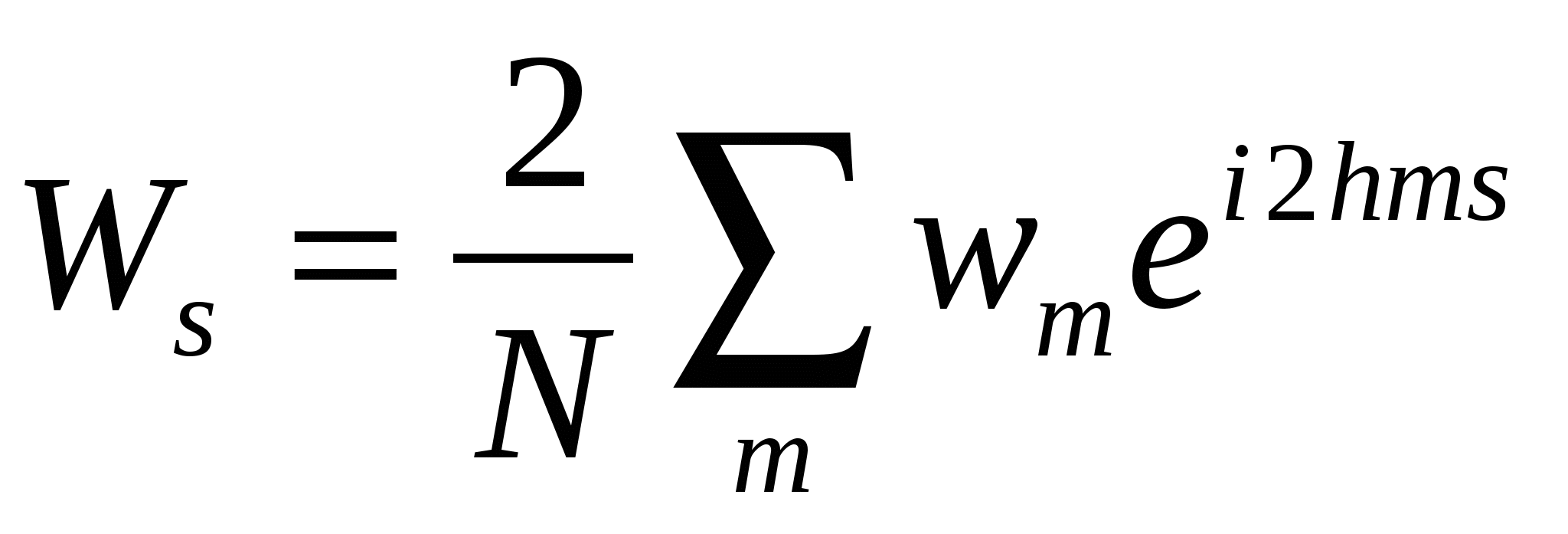
| (2.34) |
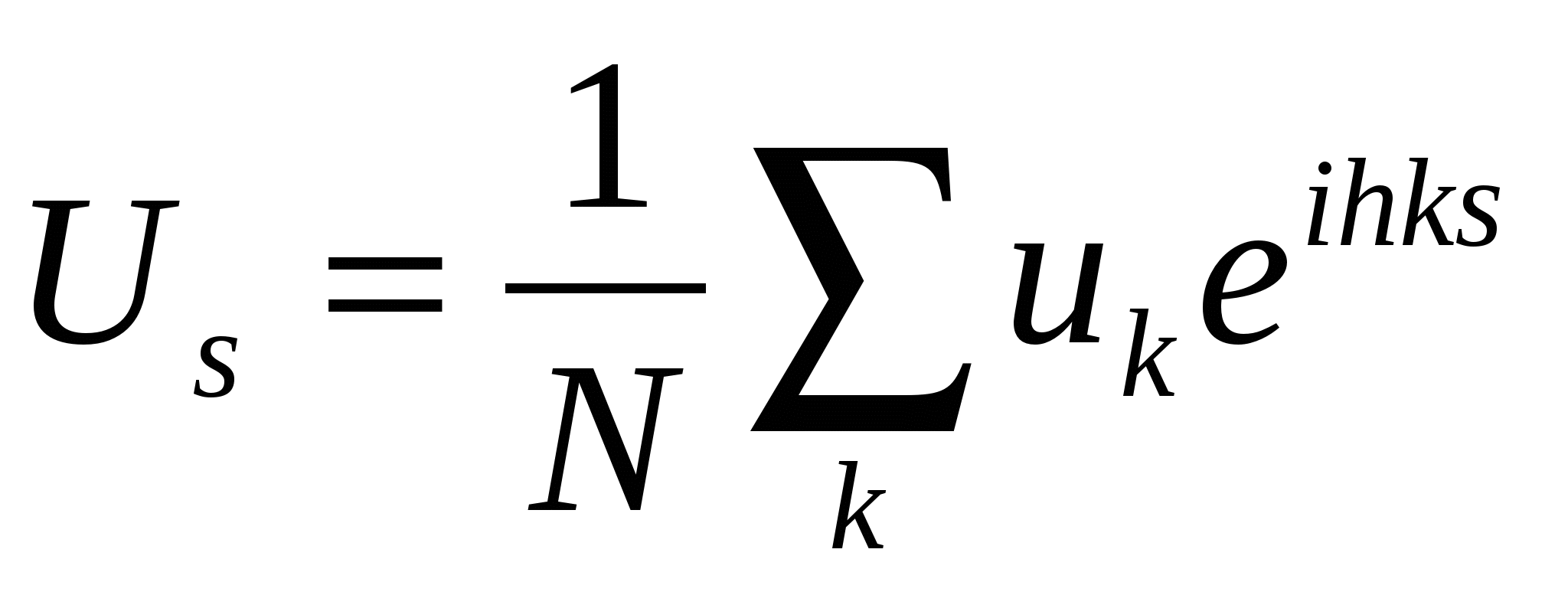
| (2.35) |
Здесь суммы по 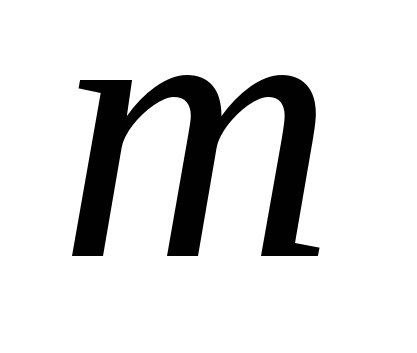 вычисляются по
вычисляются по 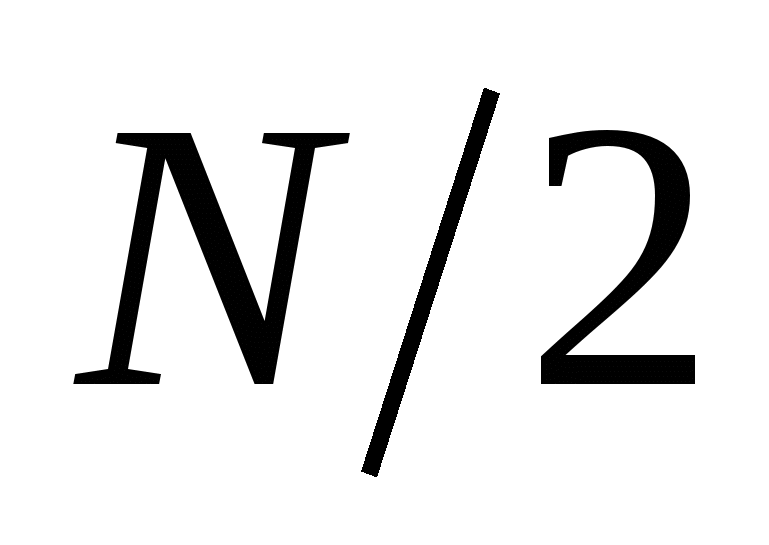 точкам и по этому появляются множители 2 перед суммой и в показателе степени. Количество гармоник в (2.33 – 2.34) равно
точкам и по этому появляются множители 2 перед суммой и в показателе степени. Количество гармоник в (2.33 – 2.34) равно 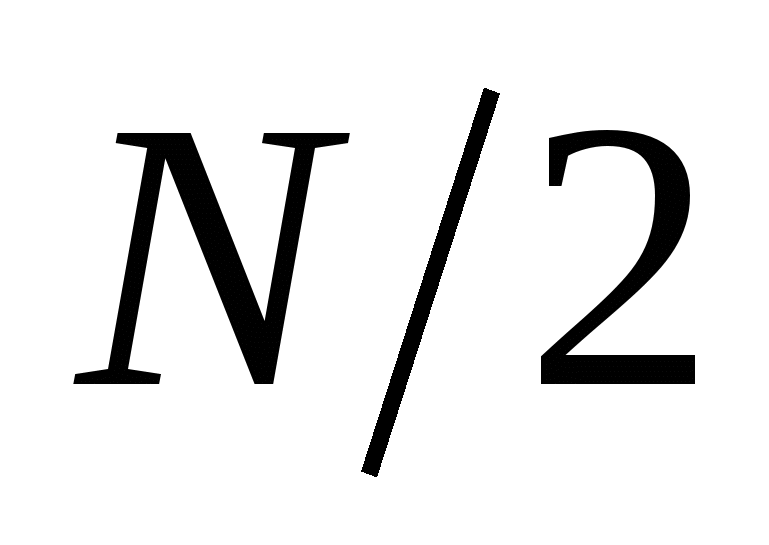 , а в (2.35) оно равно
, а в (2.35) оно равно  . Покажем, как спектр
. Покажем, как спектр 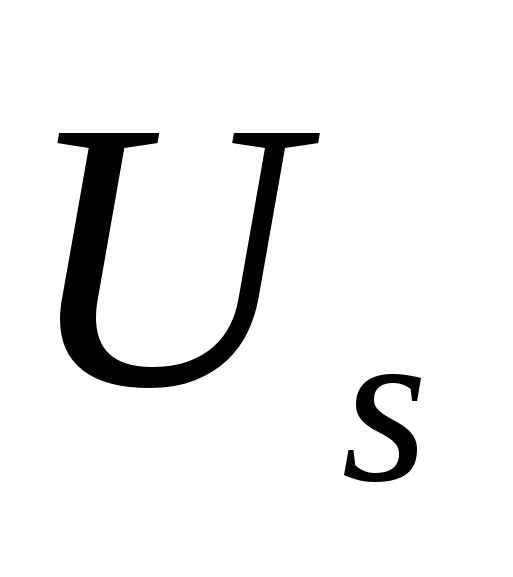 можно вычислить по спектрам
можно вычислить по спектрам 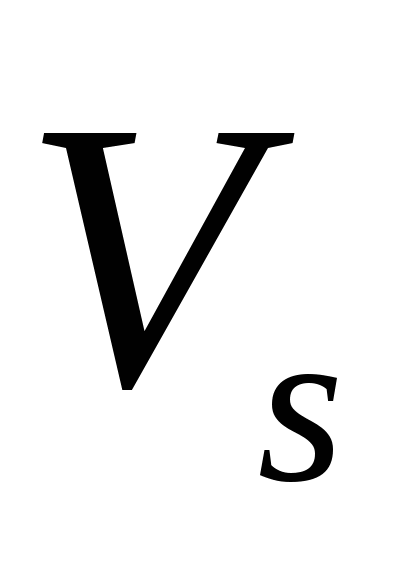 и
и 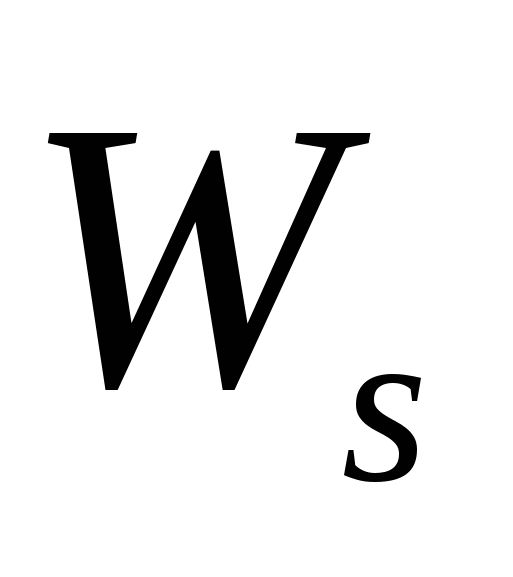 :
:
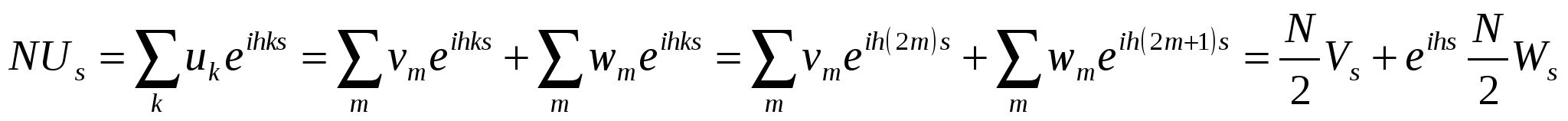 , ,
| (2.36) |
т.е. 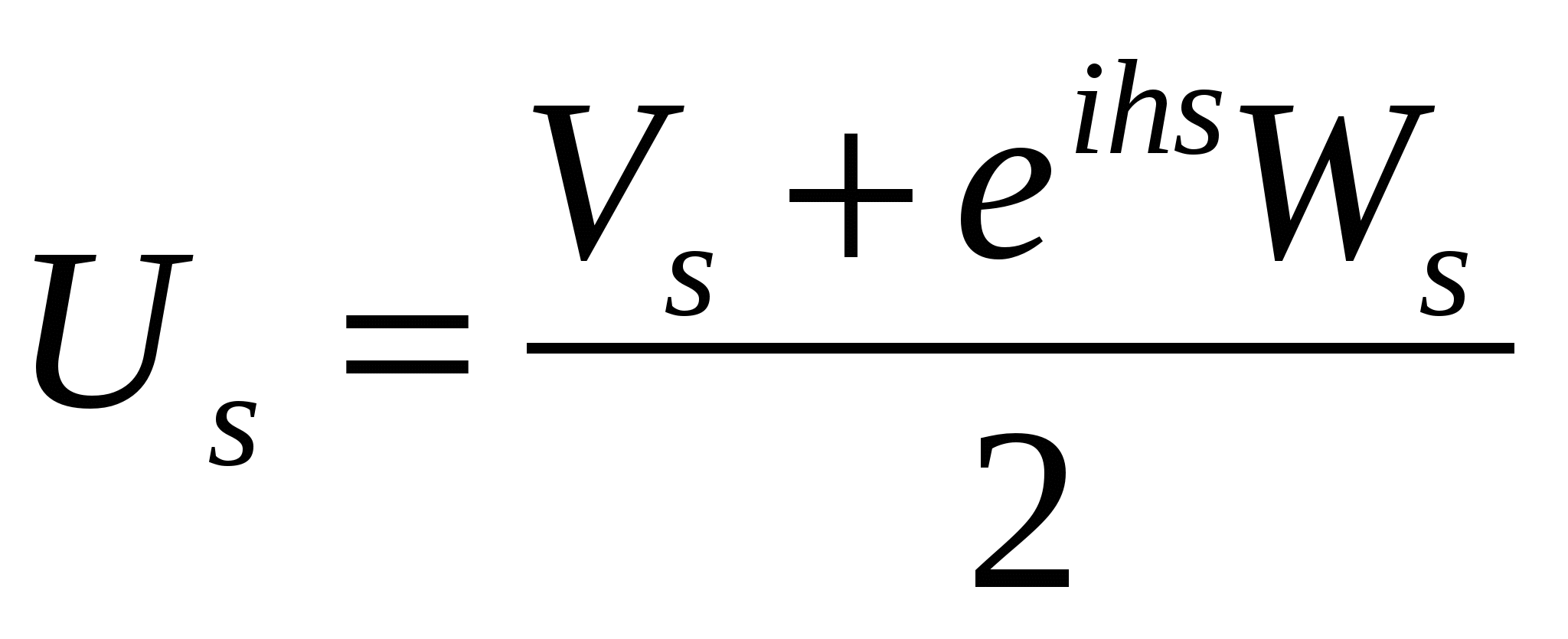 ,
, 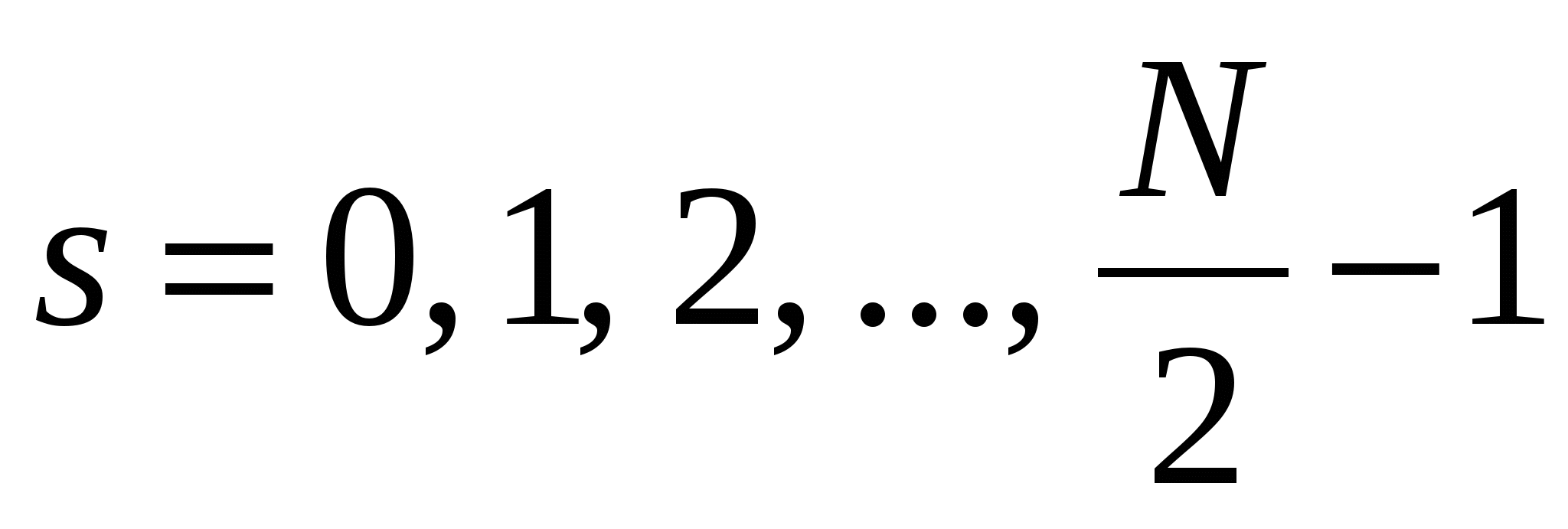 .
.
При выводе вместо отсчетов с четными номерами 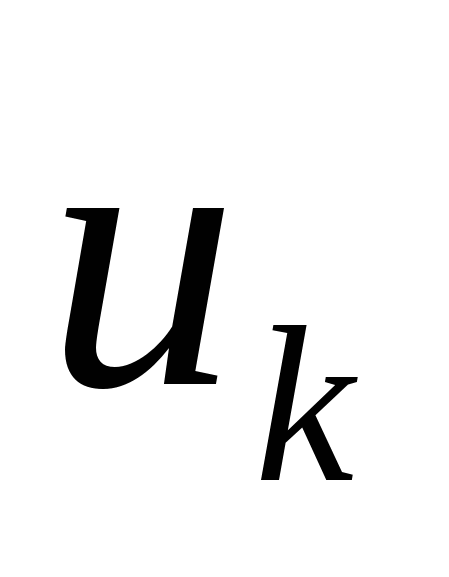 подставлены значения
подставлены значения 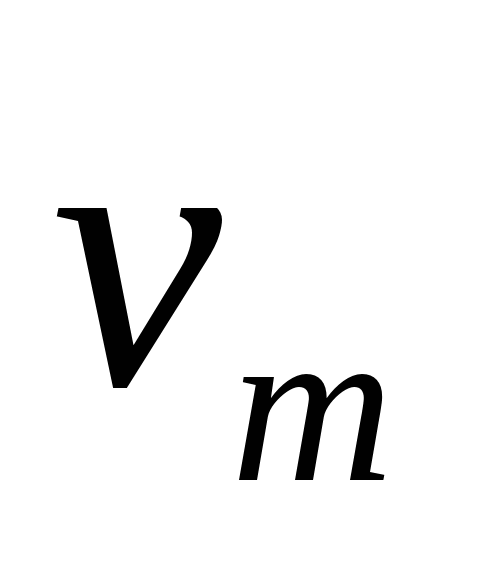 , а вместо отсчетов
, а вместо отсчетов 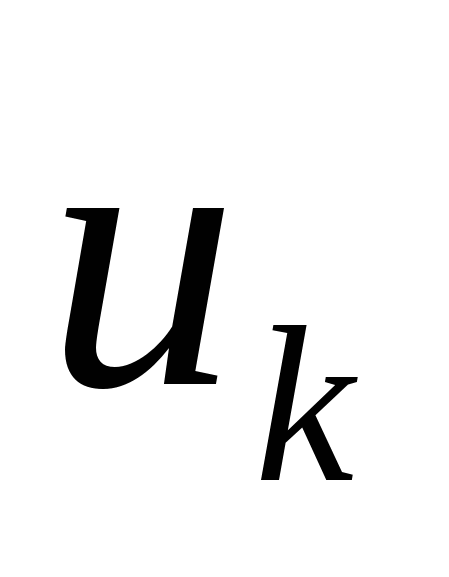 c нечетными номерами – значения
c нечетными номерами – значения 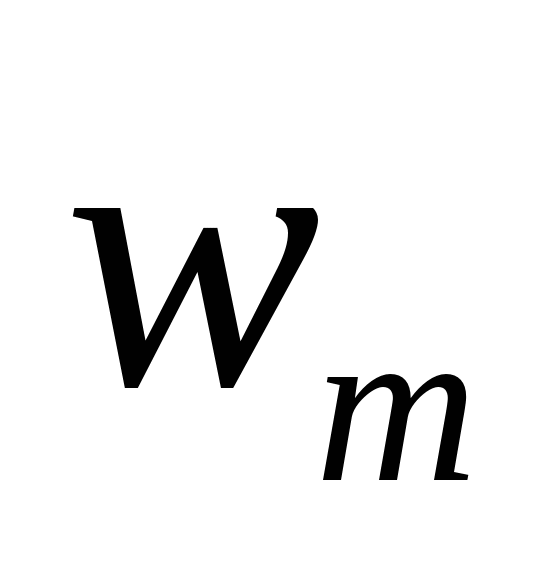 . Формулу (2.36) можно применять для
. Формулу (2.36) можно применять для 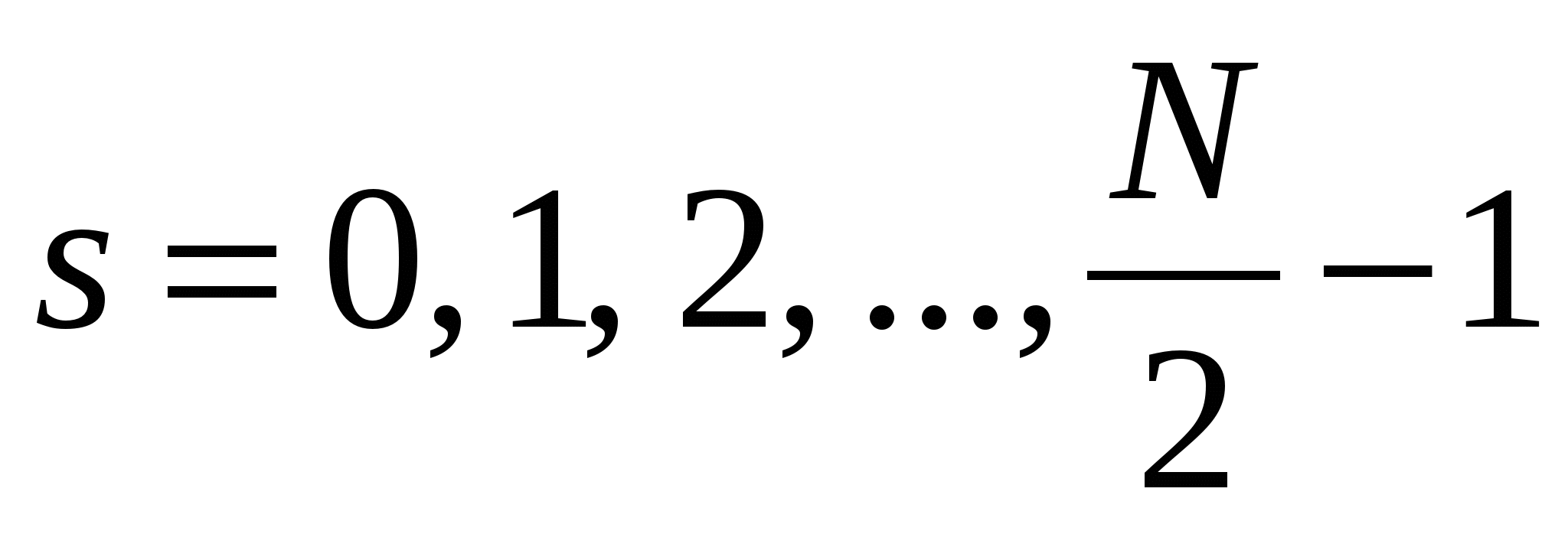 , т.к. спектры
, т.к. спектры 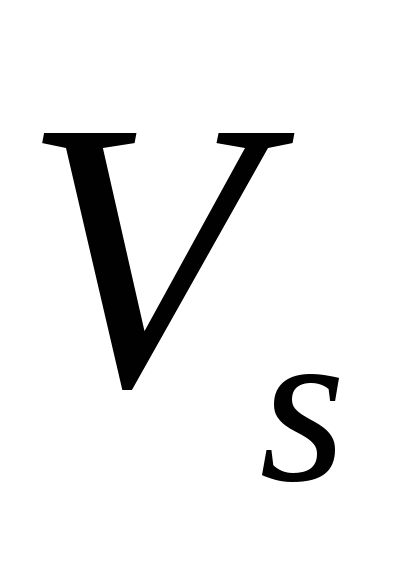 и
и 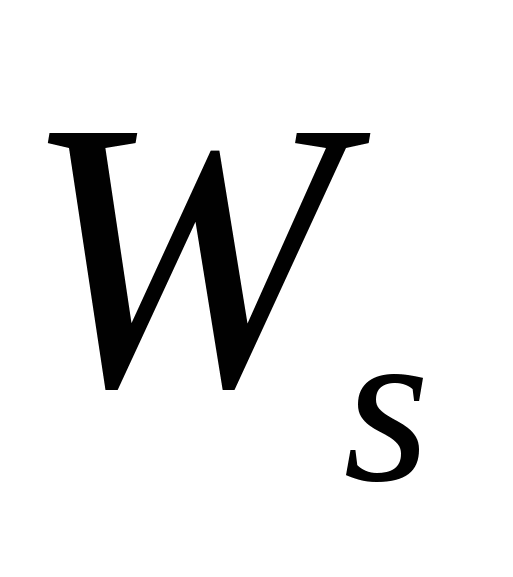 содержат
содержат 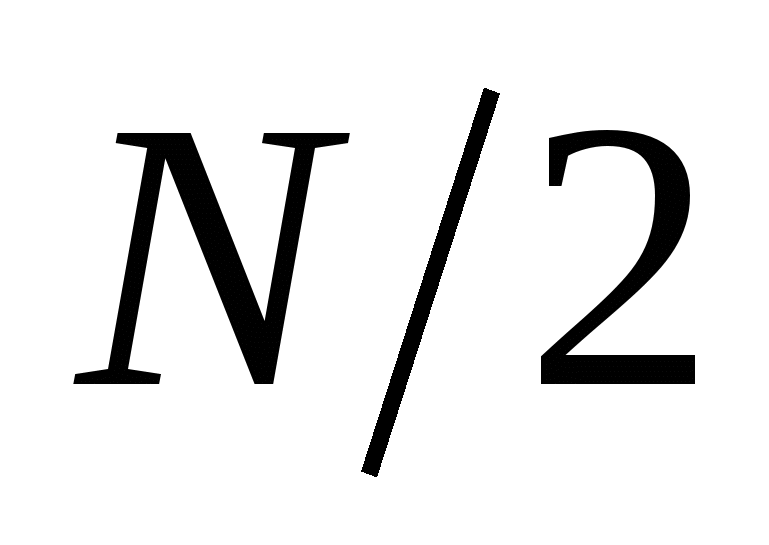 гармоник. Но учитывая их периодичность:
гармоник. Но учитывая их периодичность: 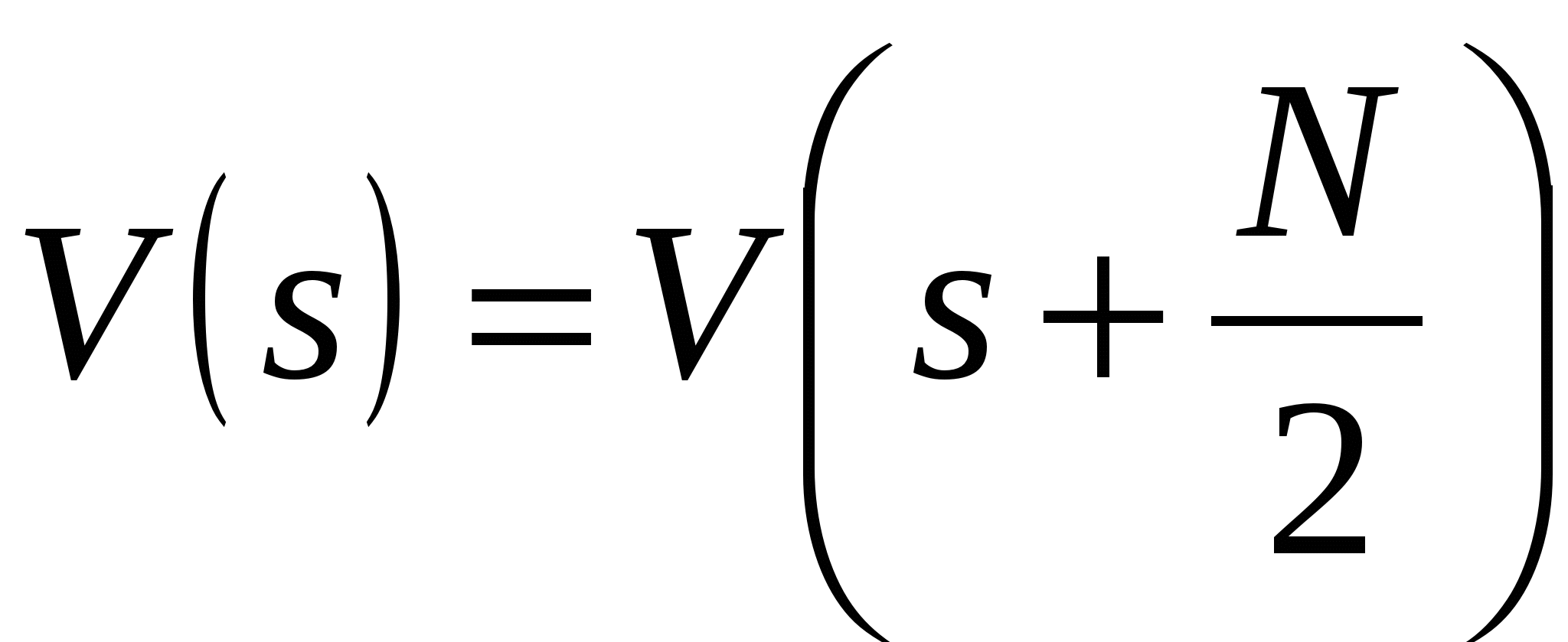 ,
, 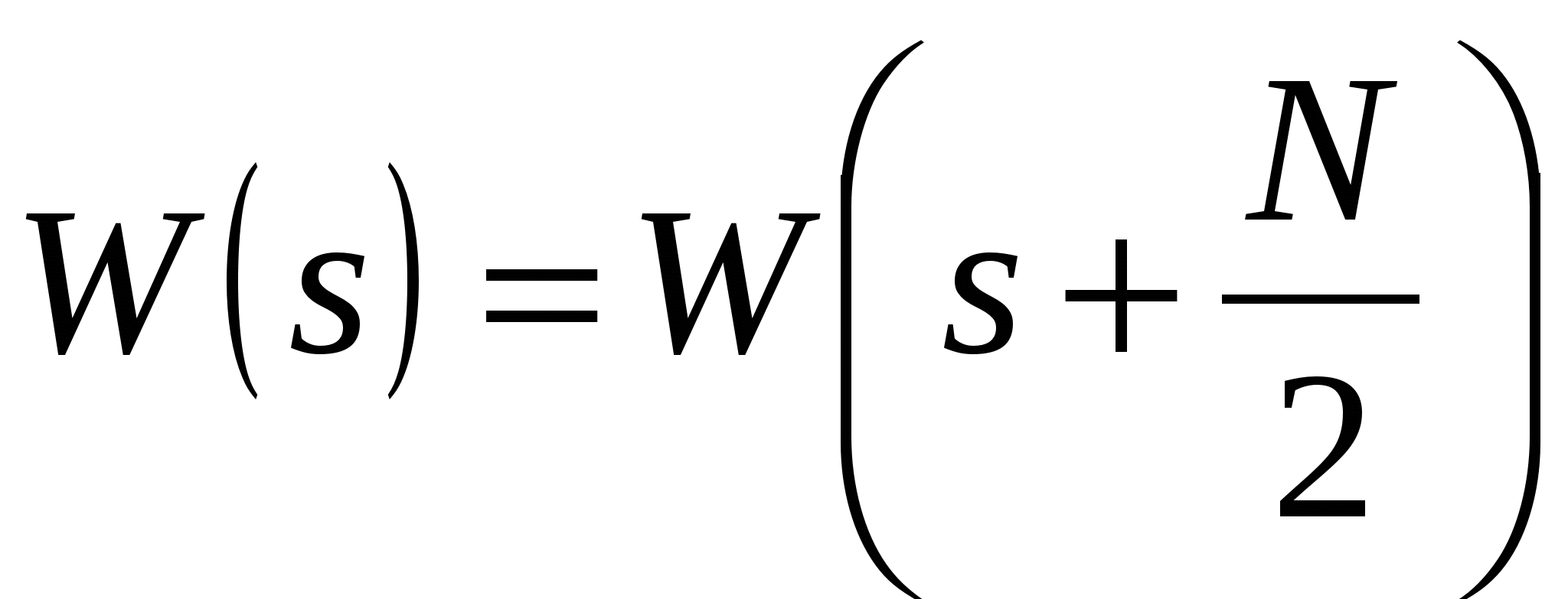 а также равенство
а также равенство 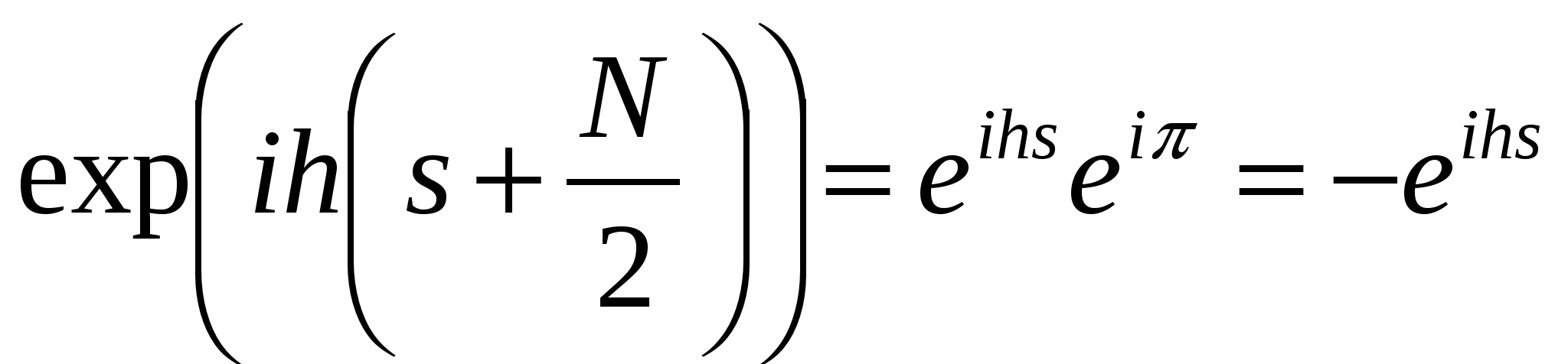 , получаем для гармоник с номерами
, получаем для гармоник с номерами 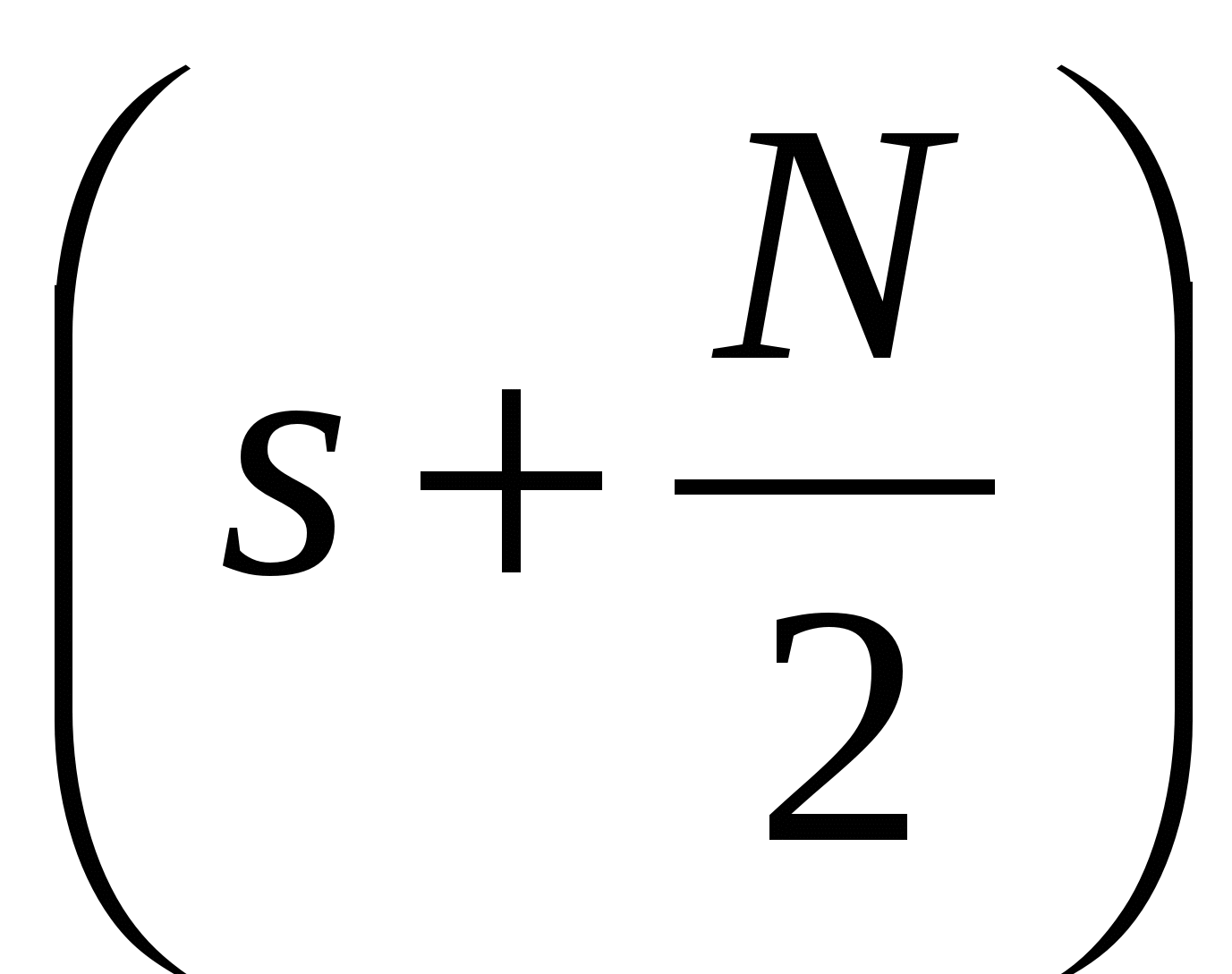
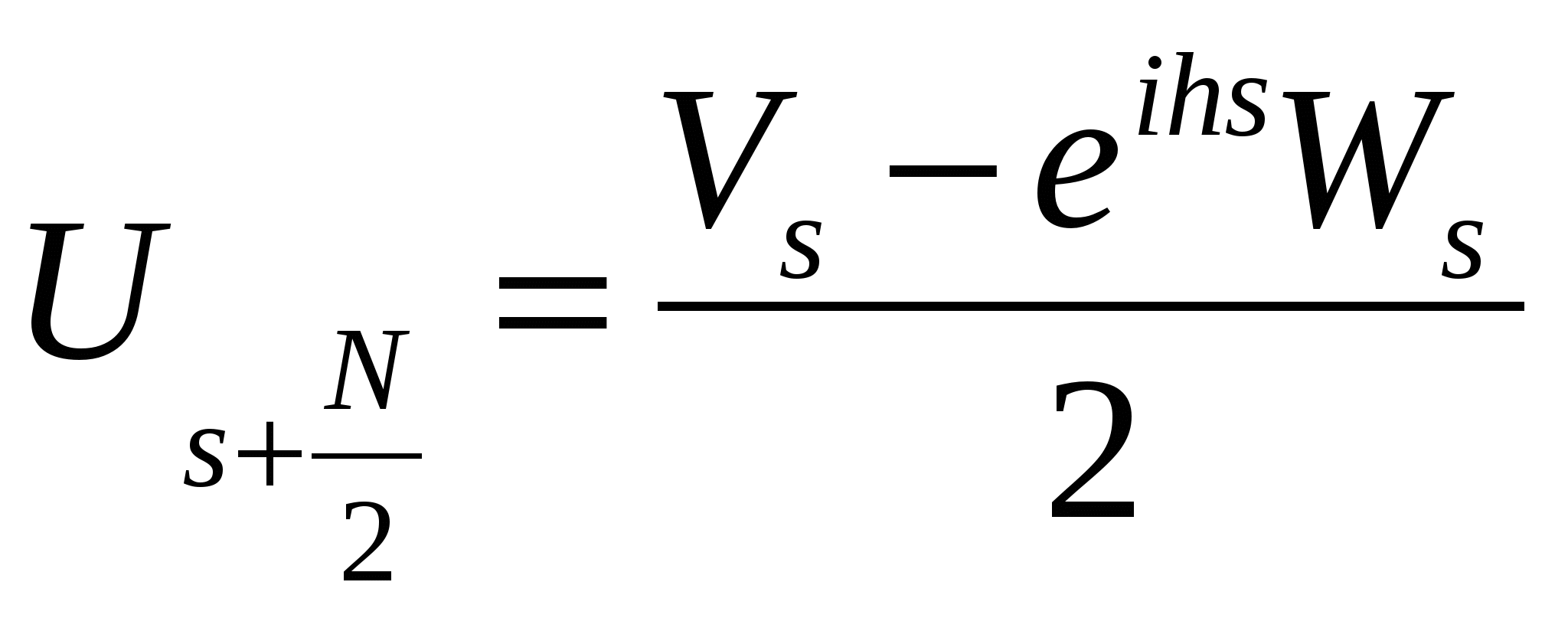
| (2.37) |
Формулы (2.36-2.37) составляют суть алгоритма “бабочка”, т.к. для его иллюстрации используют рисунок, похожий на бабочку.
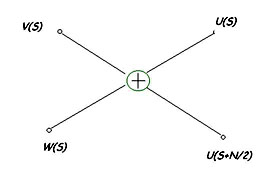
|
| Рис.2.7 Иллюстрация к алгоритму “бабочка”. |
Алгоритм БПФ
Дан массив 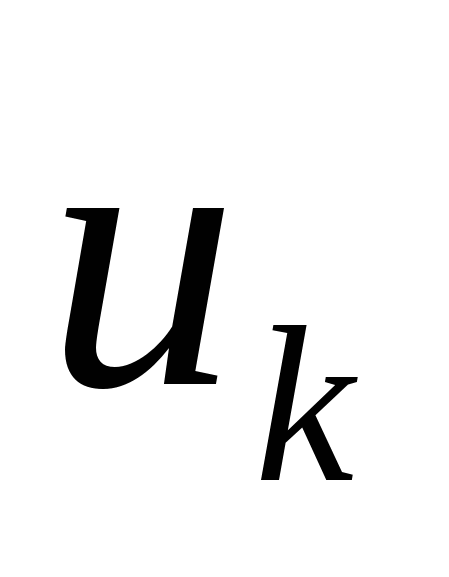 из
из  отсчетов сигнала, причем
отсчетов сигнала, причем 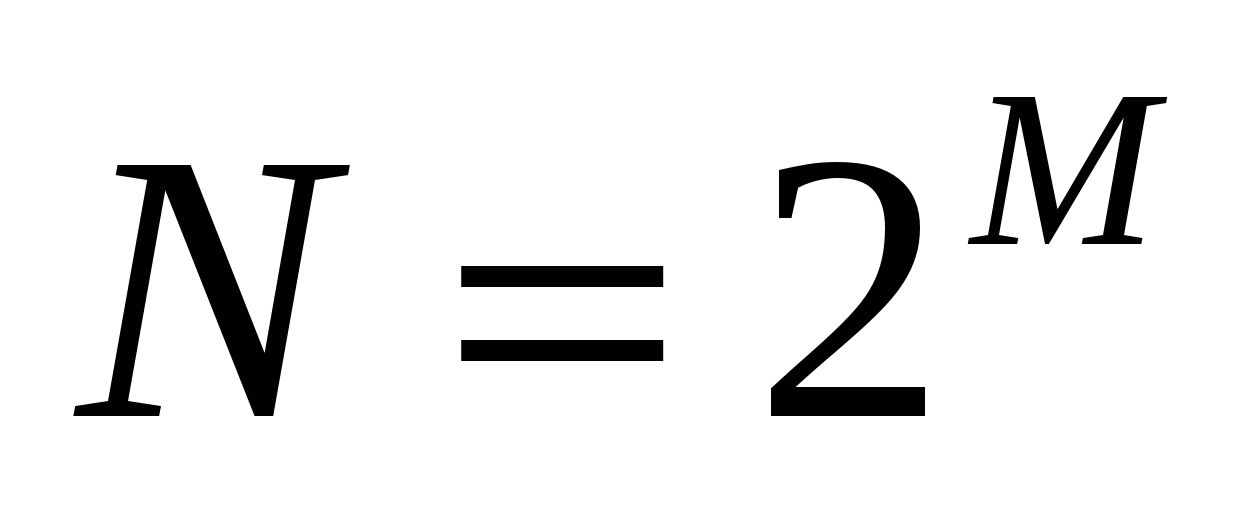 .
.
1. Расщепляем его многократно на четные и нечетные последовательности до получения  последовательностей из одного отсчета в каждой, см. рис 13.3.
последовательностей из одного отсчета в каждой, см. рис 13.3.
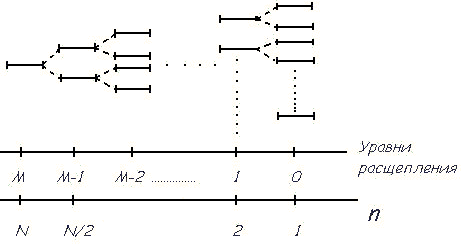
|
| Рис.2.8 Расщепление последовательностей. |
На рис. 2.8 значение  дает количество отсчетов в каждой из расщепленных последовательностей. Всего уровней расщепления
дает количество отсчетов в каждой из расщепленных последовательностей. Всего уровней расщепления 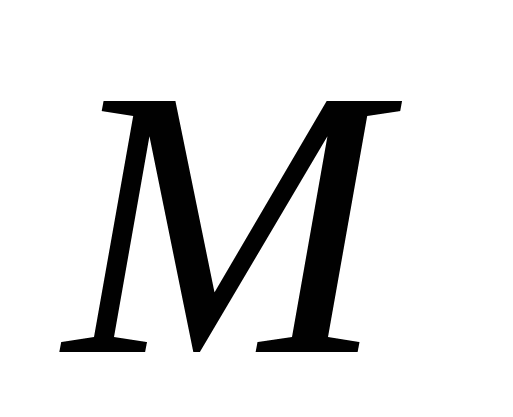 , т.е. расщепляем
, т.е. расщепляем 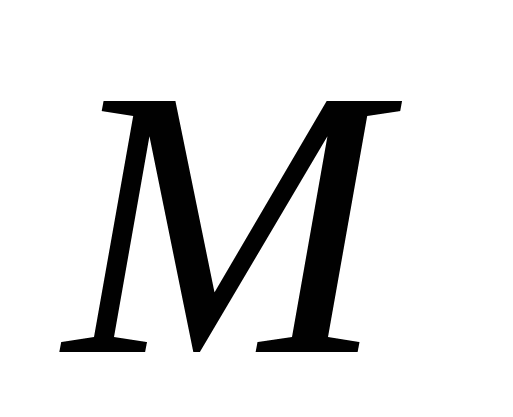 раз. Будем считать, что
раз. Будем считать, что  – это новый массив
– это новый массив  точек. В нем порядок следования точек отличен от исходного, т.е.
точек. В нем порядок следования точек отличен от исходного, т.е. 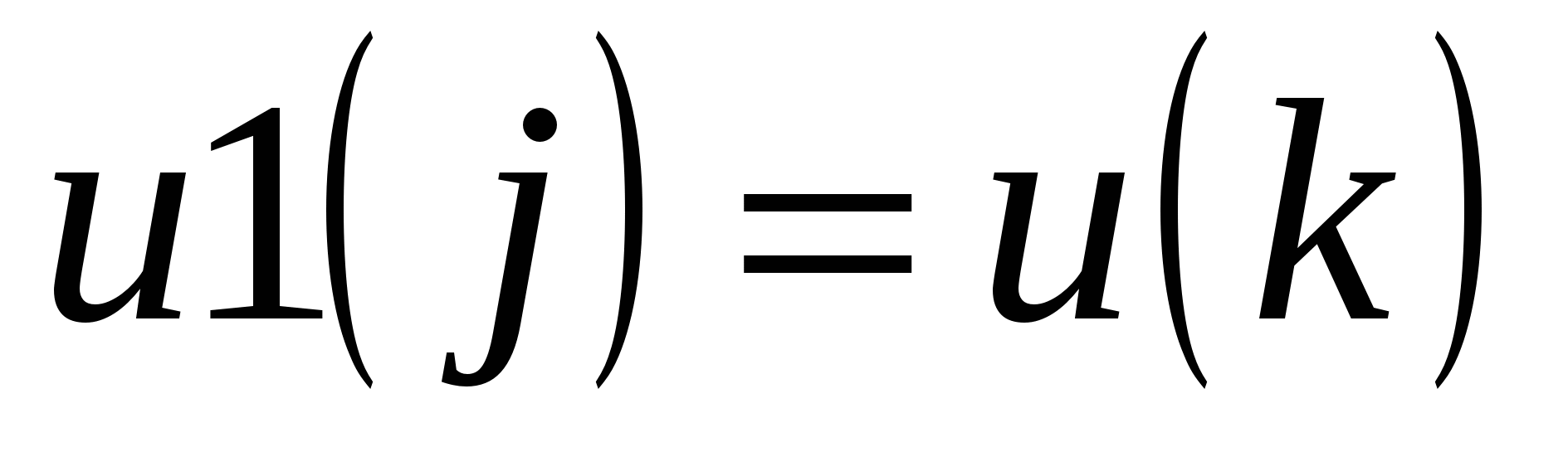 , где
, где  , а индекс
, а индекс 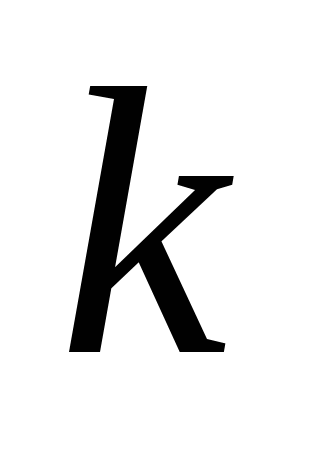 вычисляется по
вычисляется по 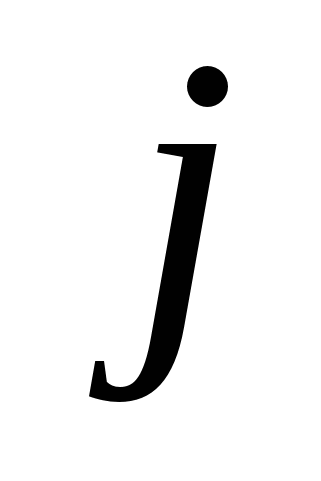 .
.
Оказывается, что преобразование  дает обратный битовый порядок, например,
дает обратный битовый порядок, например,  .
.
Для 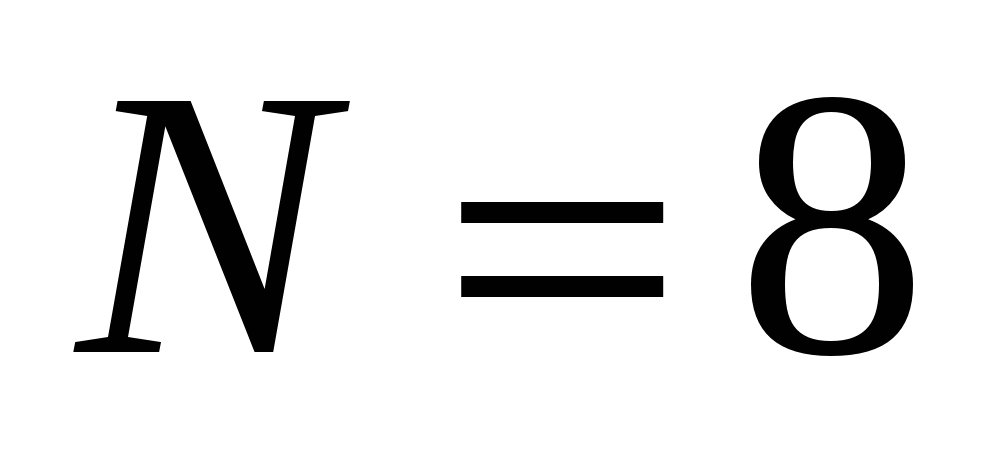 получаем следующее преобразования индексов:
получаем следующее преобразования индексов:
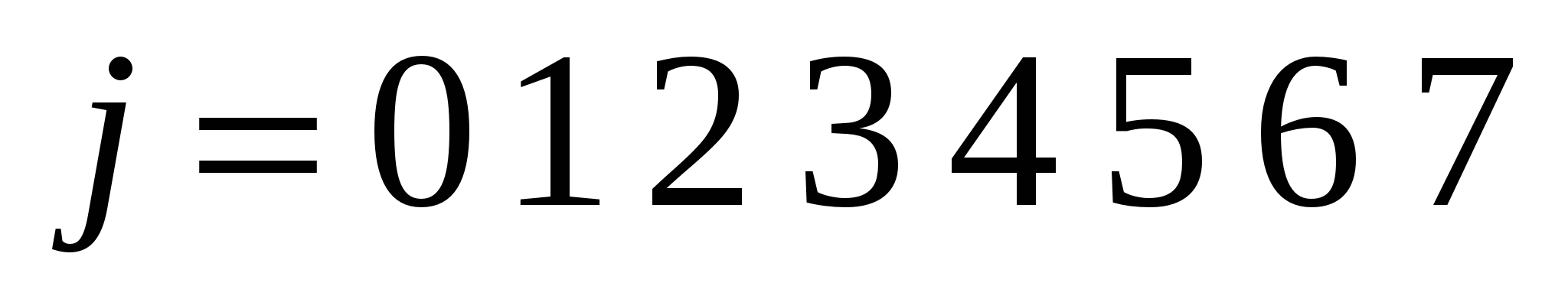
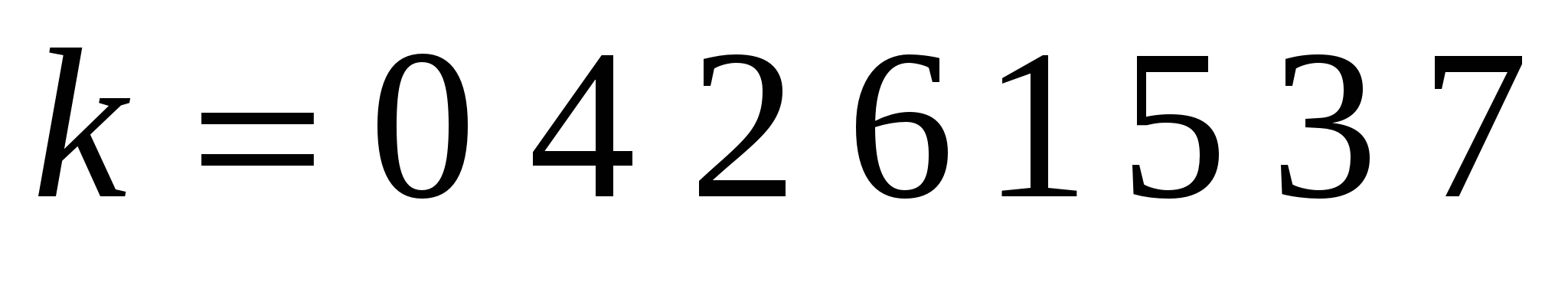
Столь простое преобразование можно не учитывать при оценках времени работы алгоритма.
2. Так как при 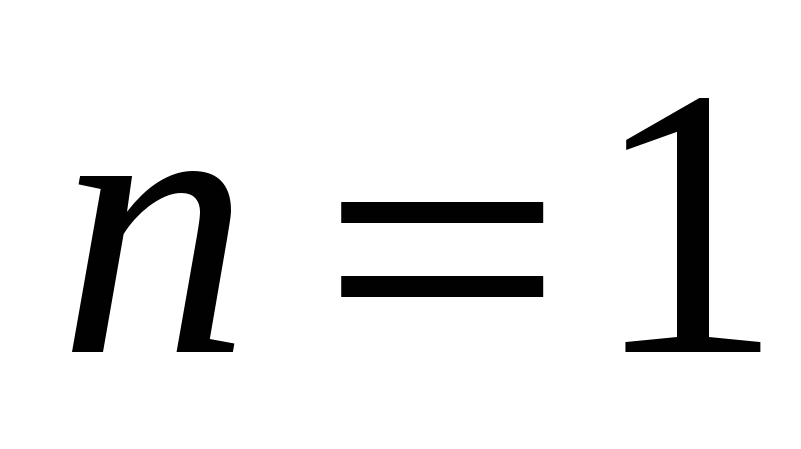 , т.е. при одном отсчете на периоде, спектр равен самому отсчету, то на последнем уровне расщепления (
, т.е. при одном отсчете на периоде, спектр равен самому отсчету, то на последнем уровне расщепления ( 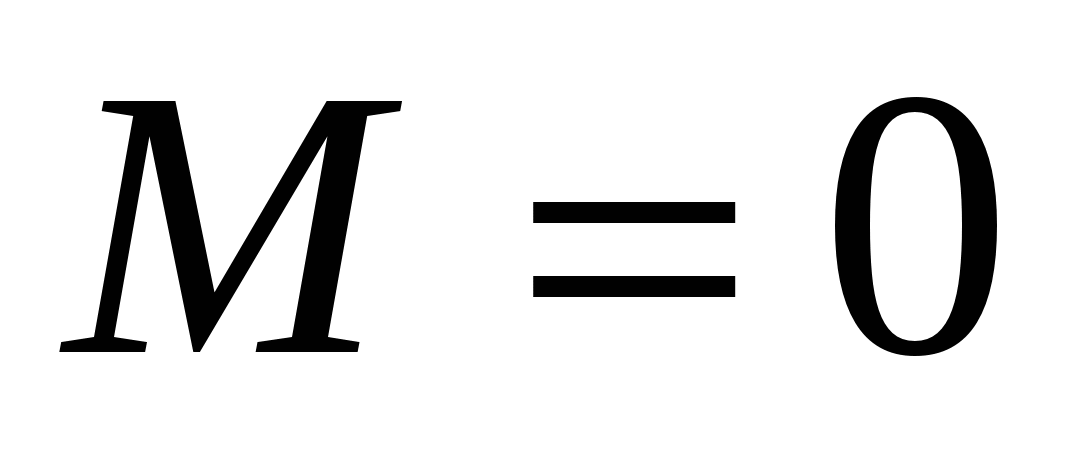 ) спектры всех
) спектры всех  последовательностей известны. Всего имеем
последовательностей известны. Всего имеем  спектров, каждый из которых состоит только из нулевой гармоники (
спектров, каждый из которых состоит только из нулевой гармоники ( 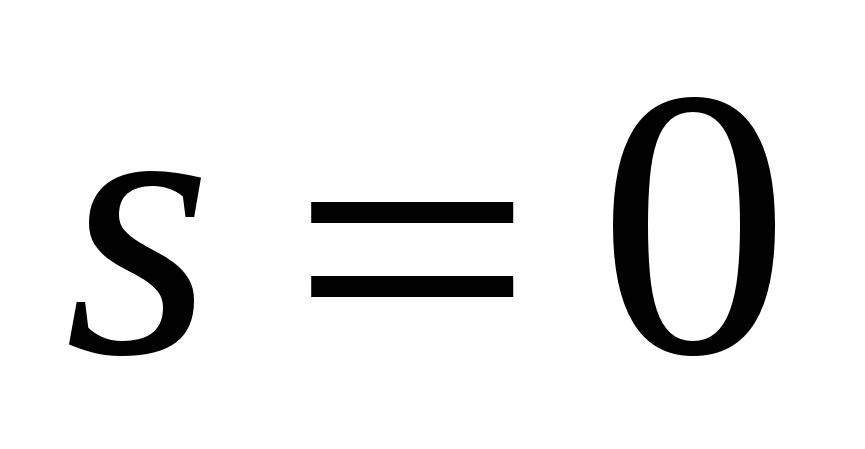 ), т.е. среднее значение.
), т.е. среднее значение.
3. Объединение последовательностей, т.е. обратный ход.
При каждом объединении используются формулы для вычисления спектра (13.4-13.5). Вычисления завершаются после получения спектра 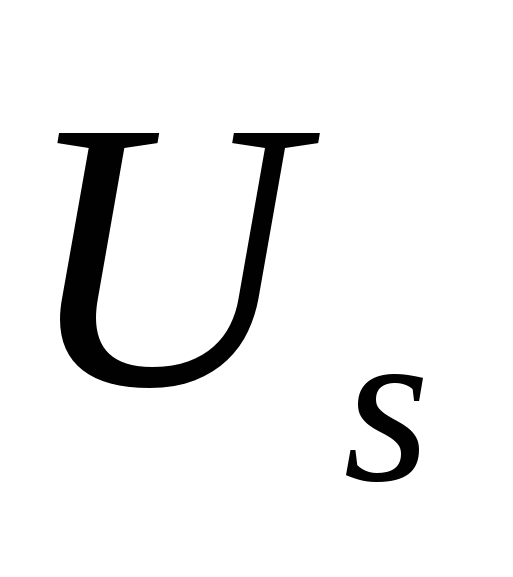 из
из  гармоник для исходной последовательности уровня
гармоник для исходной последовательности уровня 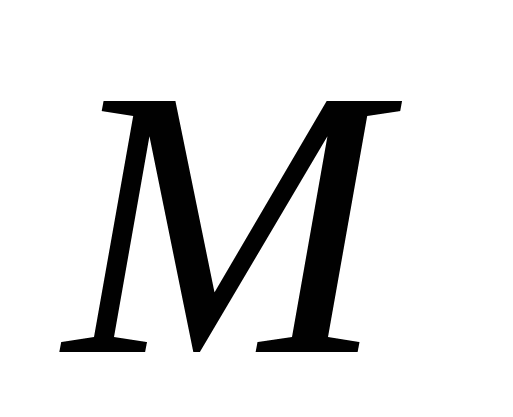 .
.
Дата добавления: 2016-02-20; просмотров: 1009;
