Количество операций в ДПФ.

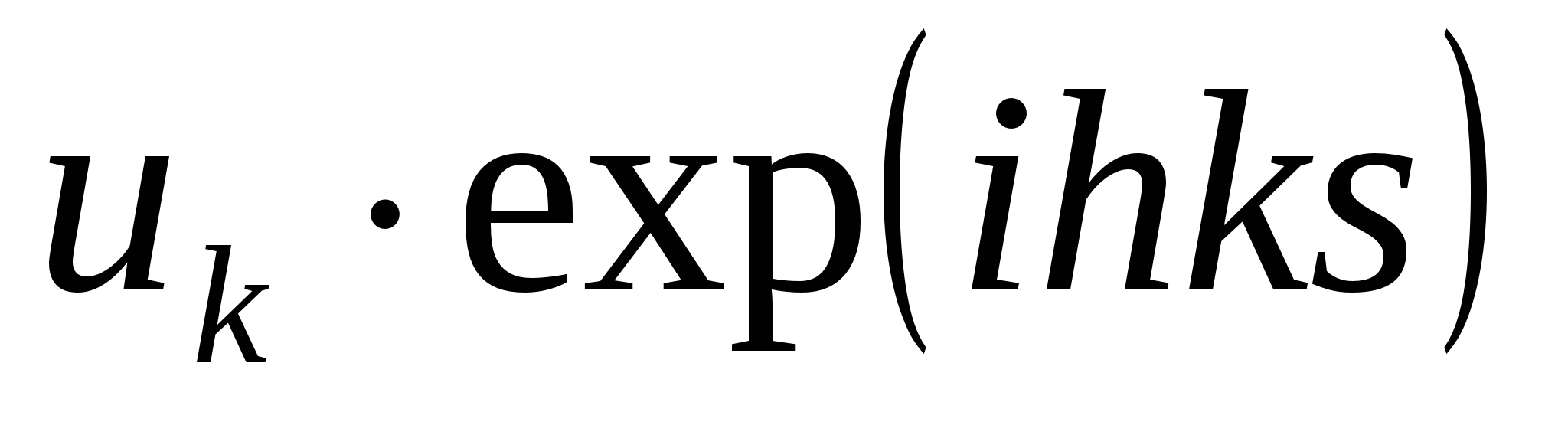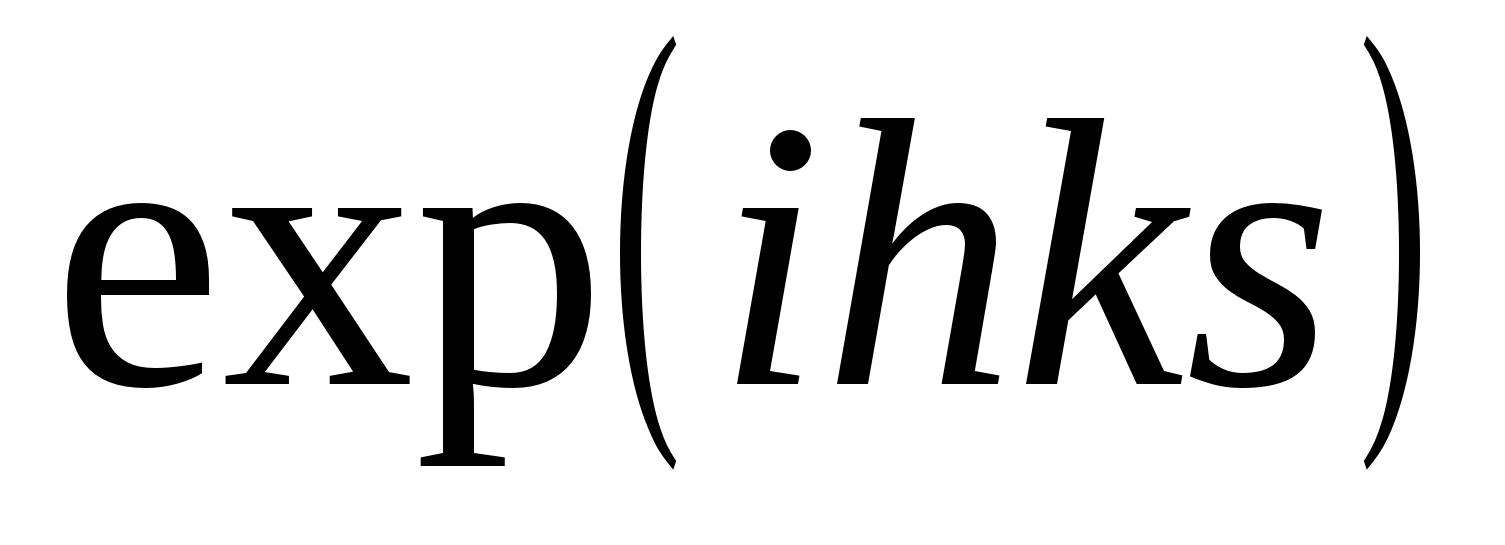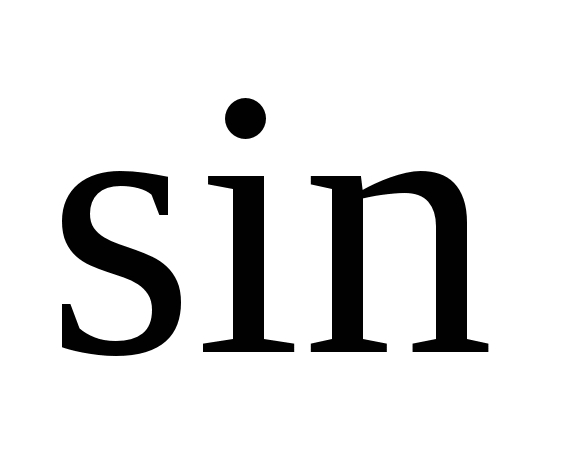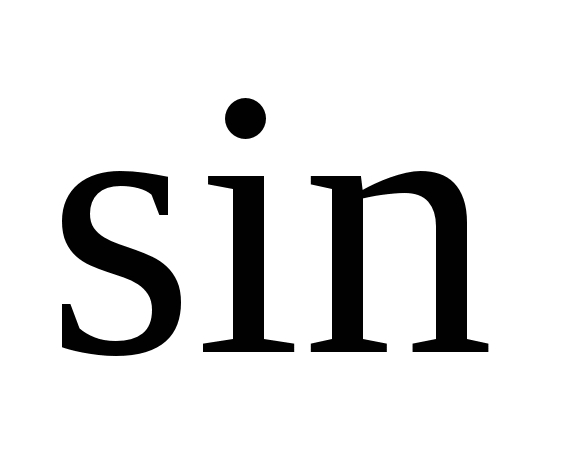Оценим количество операций по (2.31). Операцией будем считать умножение на комплексную экспоненту, т.е. . Операции здесь очень сложные, т.к. вычисляется через , , а , через полиномы.
Имеем слагаемых для вычисления одной гармоники по (2.31) и поэтому для вычисления одной гармоники нужно операций. Так как всего вычисляется гармоник 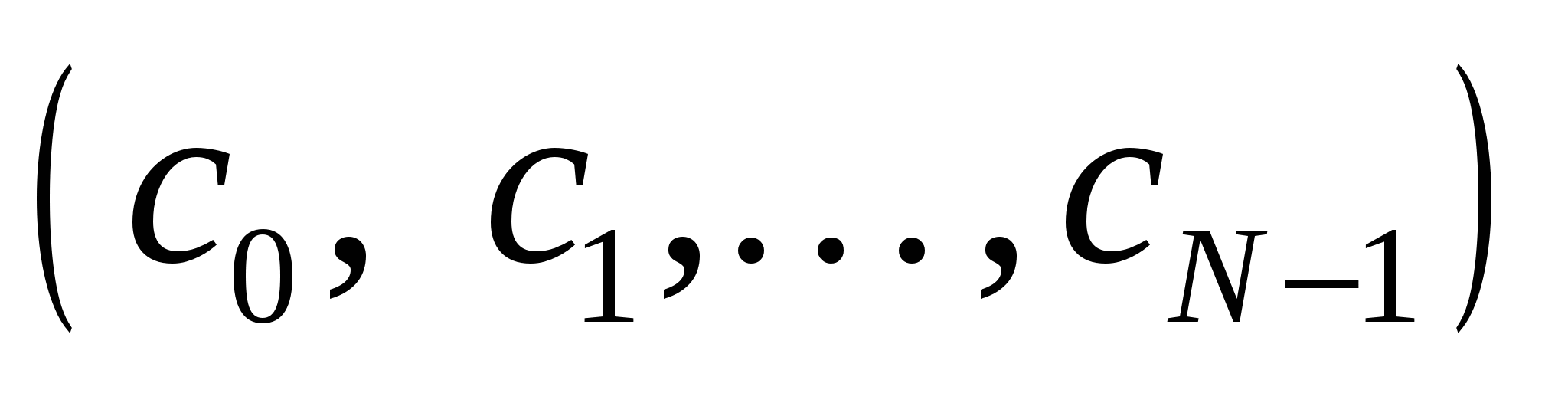, то прямое ДПФ требует примерно 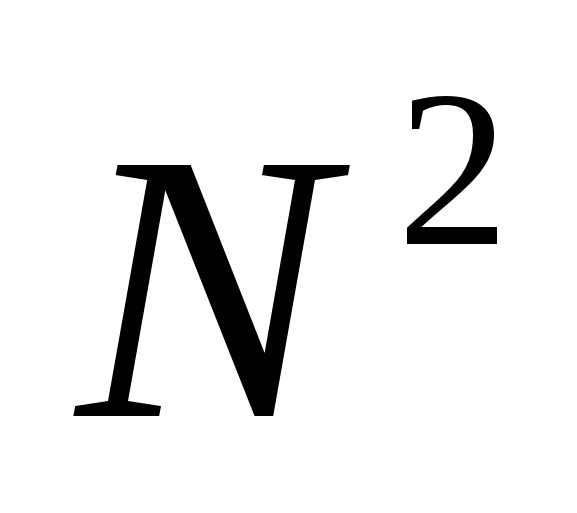операций, т.е. сложность алгоритма ДПФ 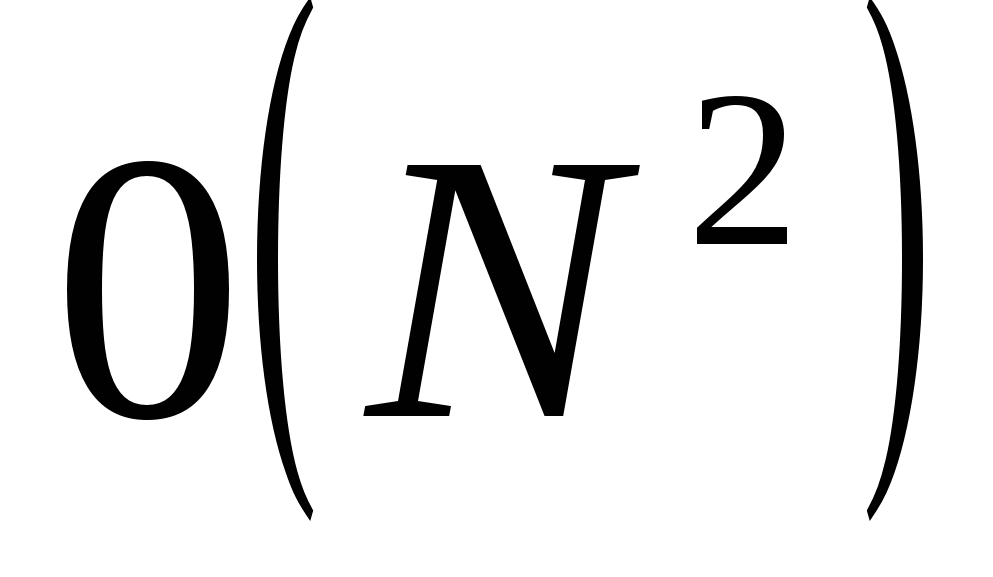. Это означает, что при увеличении в 10 раз, количество операций увеличится в 100 раз.

БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (БПФ)

Понятие о БПФ

БПФ – это группа алгоритмов для программной реализации ДПФ, сокращающих количество операций примерно в раз, т.е. 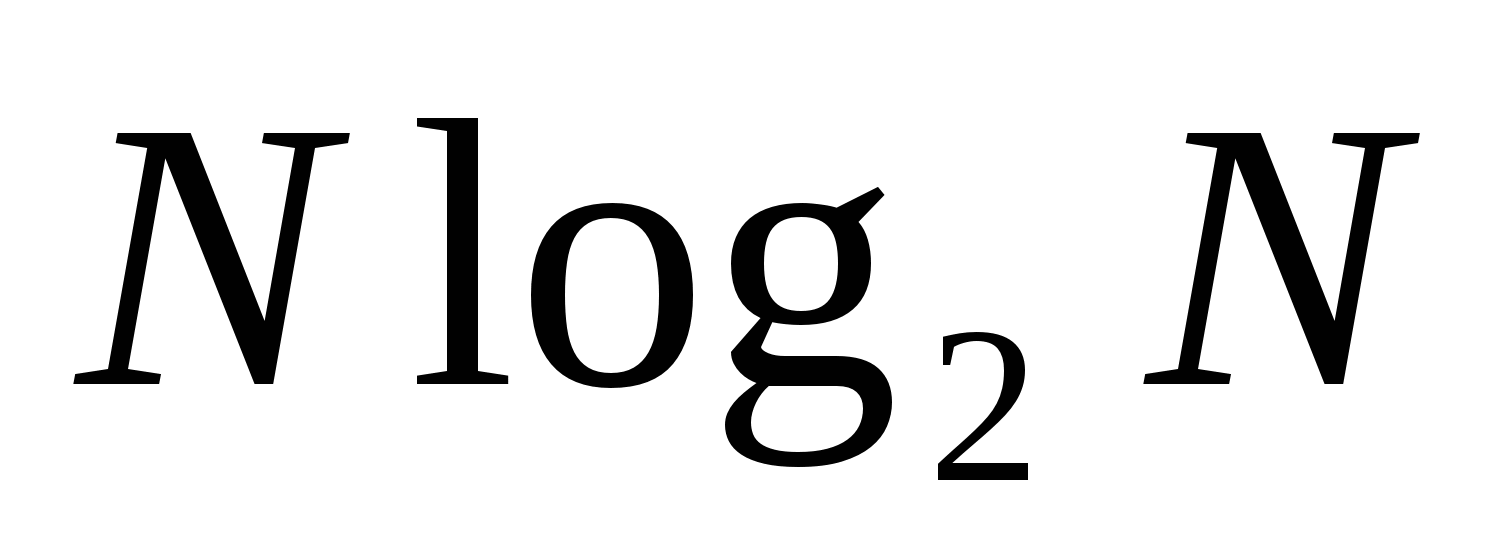операций вместо 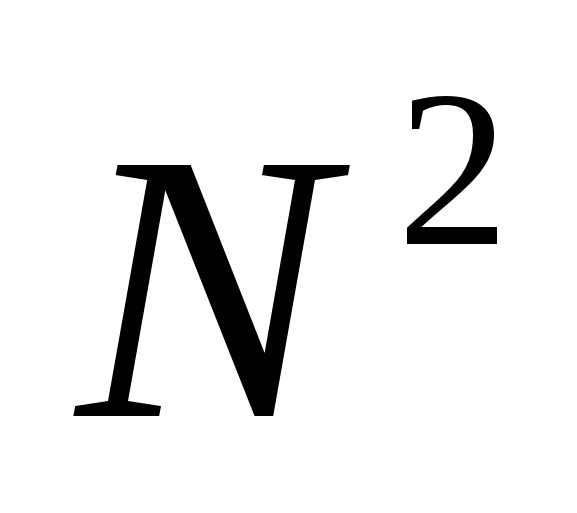. Другими словами, БПФ - это ДПФ, выполняемое очень быстро. Первый алгоритм БПФ предложен в 1965г, а сейчас их много и они очень сложные. Мы рассмотрим один из них, наиболее простой для понимания. Этот алгоритм, иногда называемый алгоритмом “бабочки”, основан на расщеплении исходного массива отсчетов сигнала. Появление БПФ сделало переворот в цифровой обработке, т.к. позволило легко переходить к преобразованиям спектров в случае больших значений .

Основу БПФ составляют 4 идеи:

1. Спектр ДПФ – периодический, .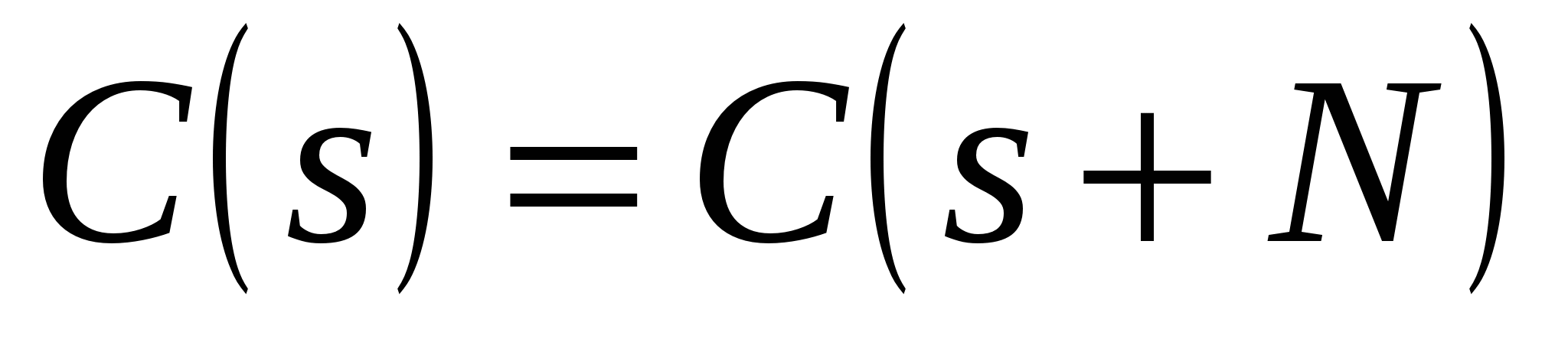
2. Спектр ДПФ легко вычисляется в случае 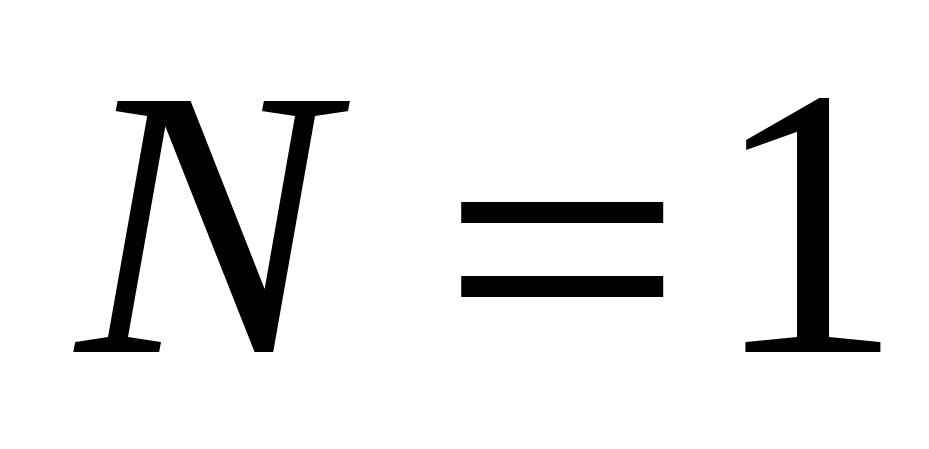, когда имеется только одна гармоника и по (14.7)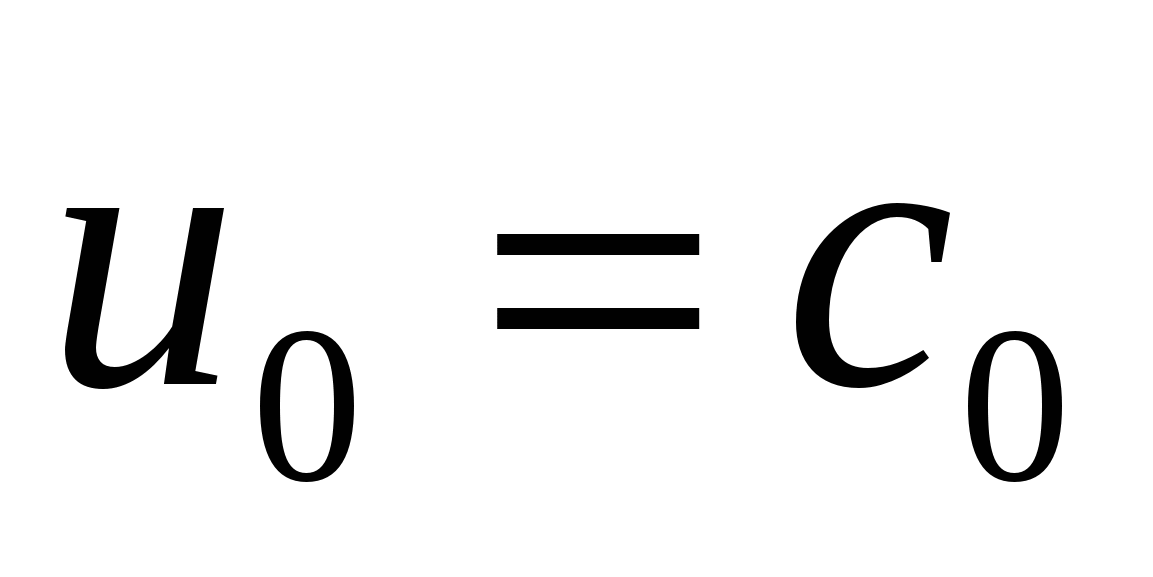
3. Выбирается 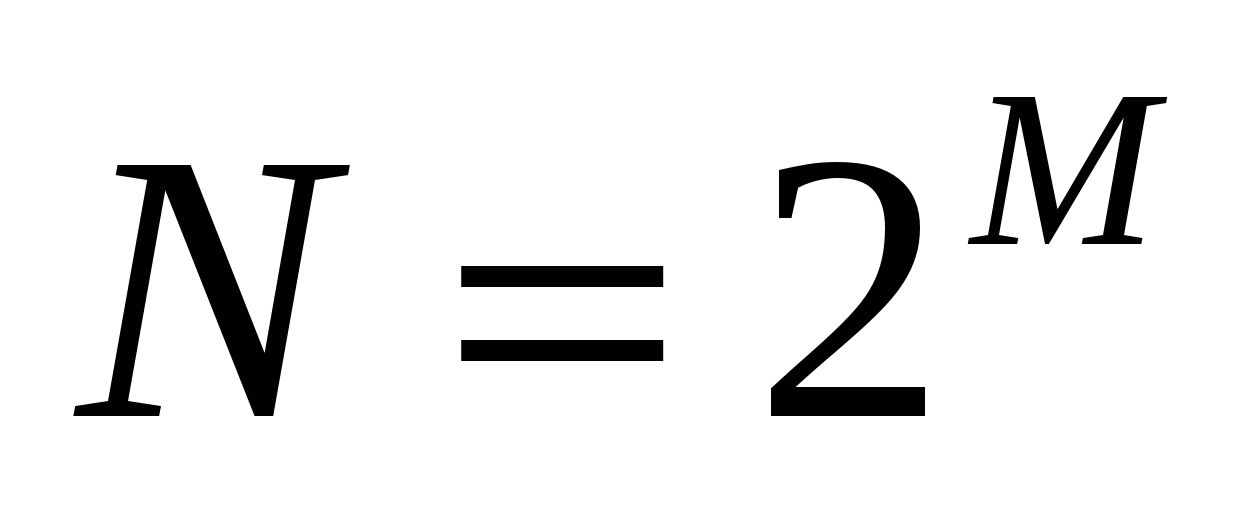, где 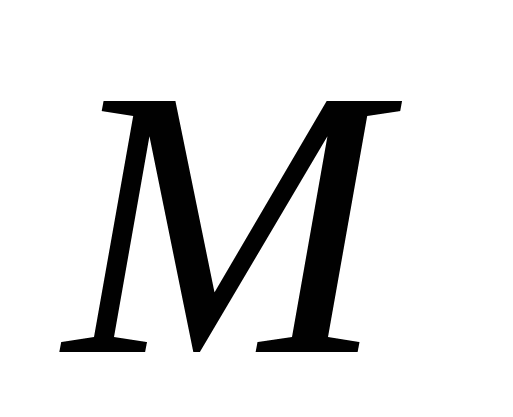– целая степень, т.е. количество отсчетов не может быть произвольным целым числом. Например, при 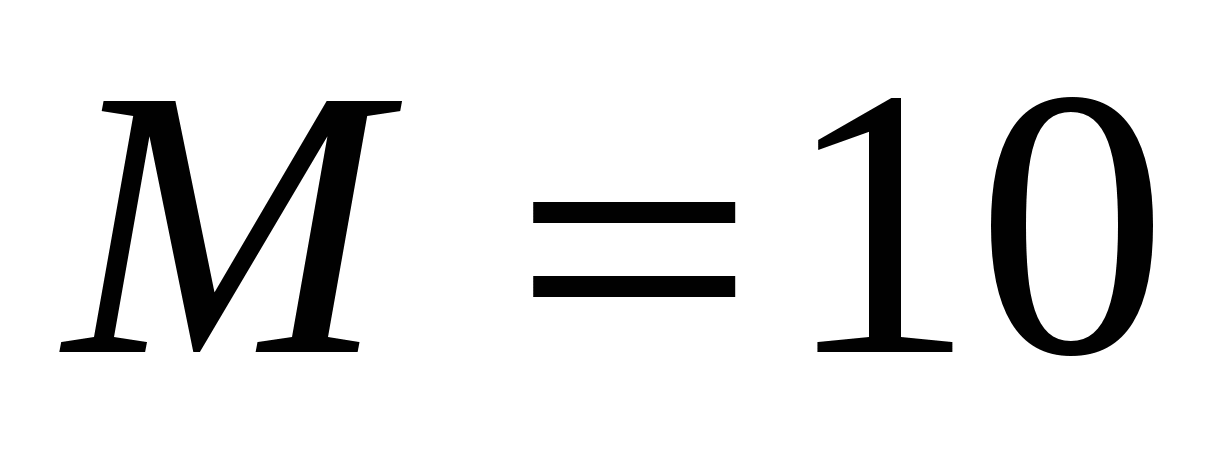имеем .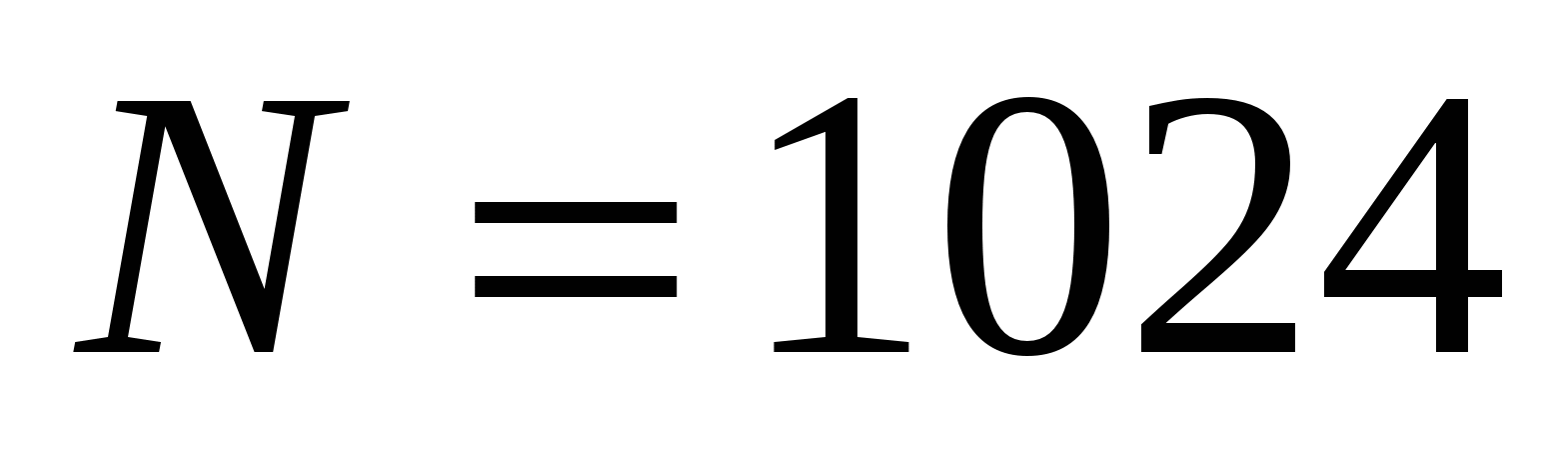
4. Спектр исходной последовательности несложно найти по спектрам расщепленных последовательностей. При каждом расщеплении от одного массива из отсчетов переходят к двум массивам из 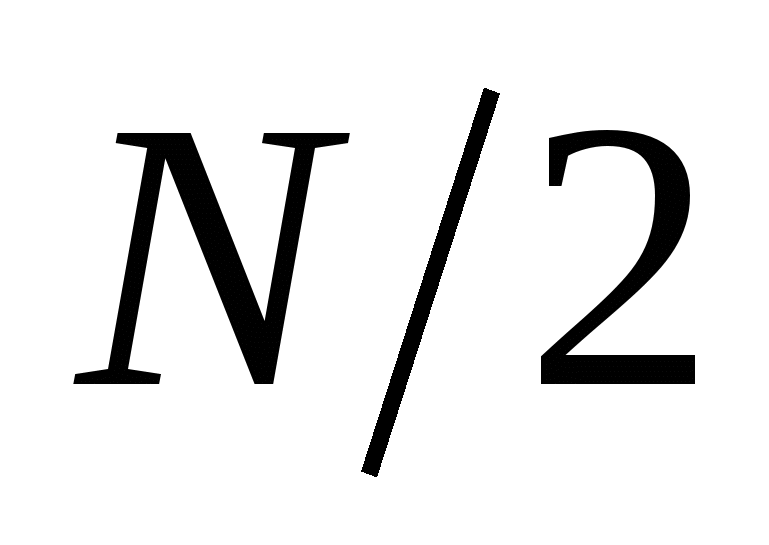отсчетов каждый.