Оценка количества операций в БПФ.

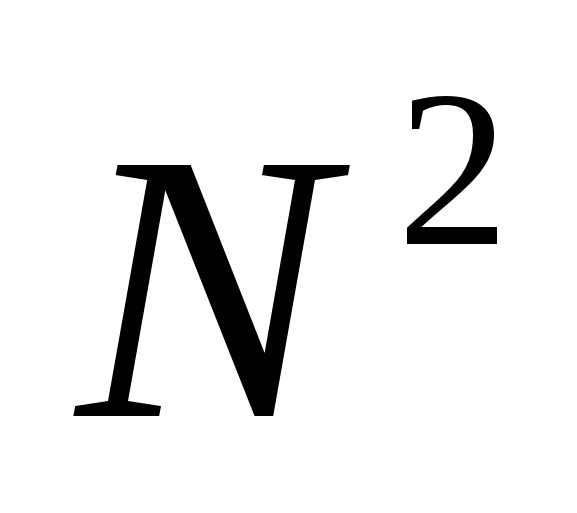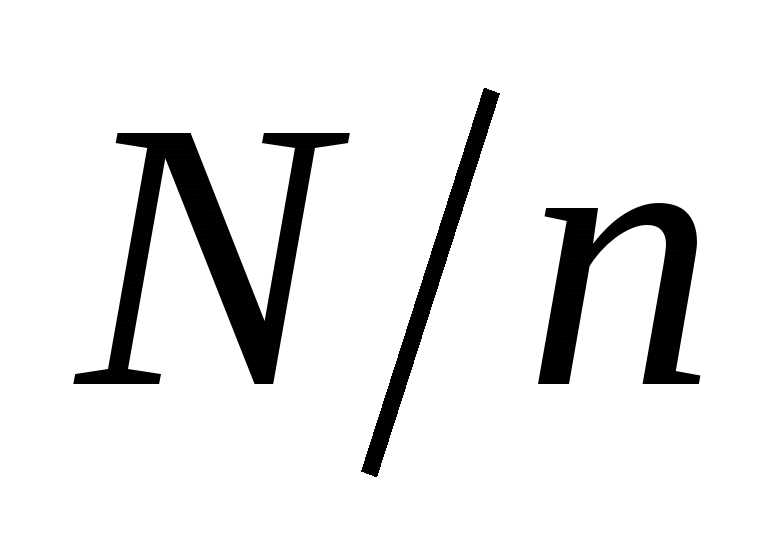В ДПФ было примерно операций, см. раздел 14.6. В БПФ одна гармоника требует одной операции в соответствии с (2.35) или (2.36). На каждом уровне расщепления вычисляется гармоник (равное числу отсчетов) для каждого из сигналов, т.е. всего гармоник. Так как количество уровней расщепления равно 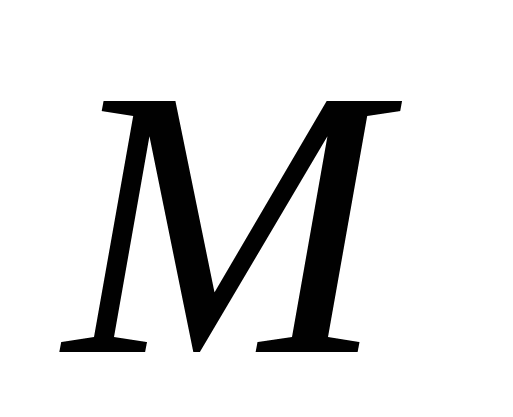, то всего нужно определить гармоник, т.е.выполнить 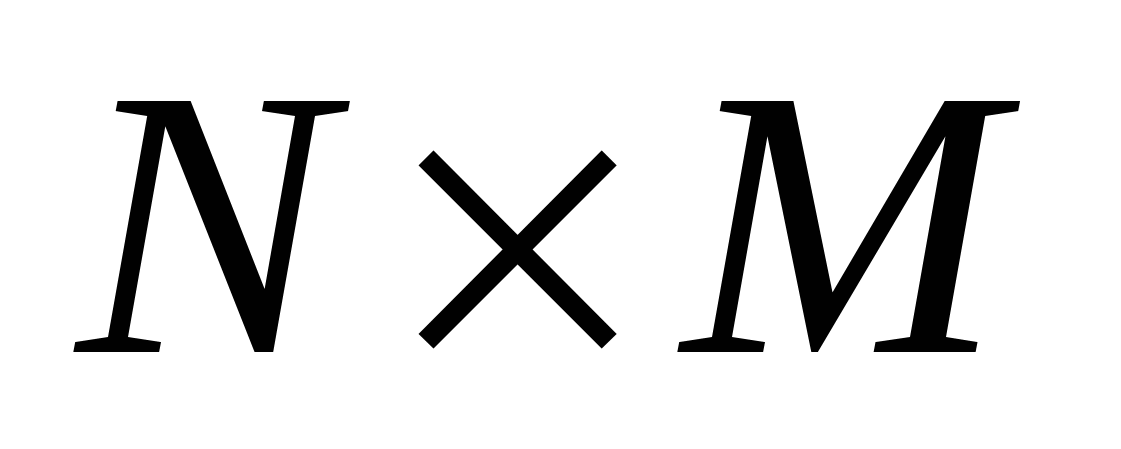операций, где 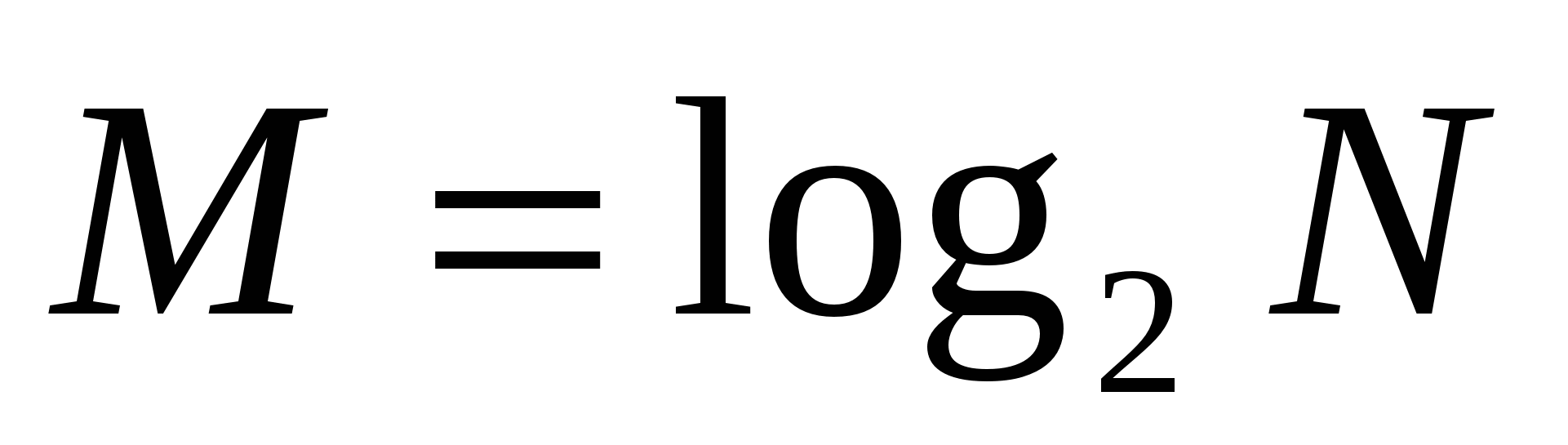. Следовательно, БПФ требует 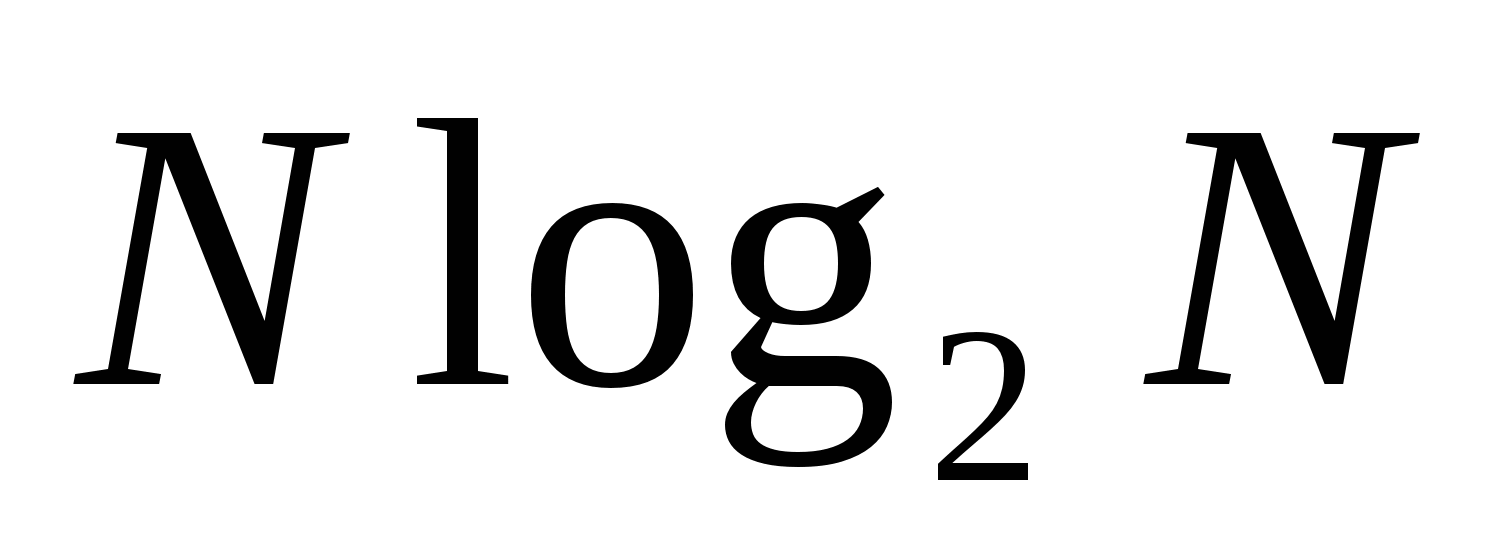операций вместо 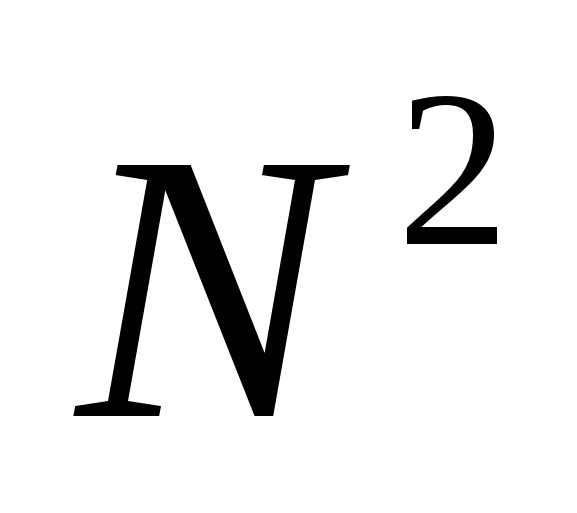в ДПФ, т.е. оно в 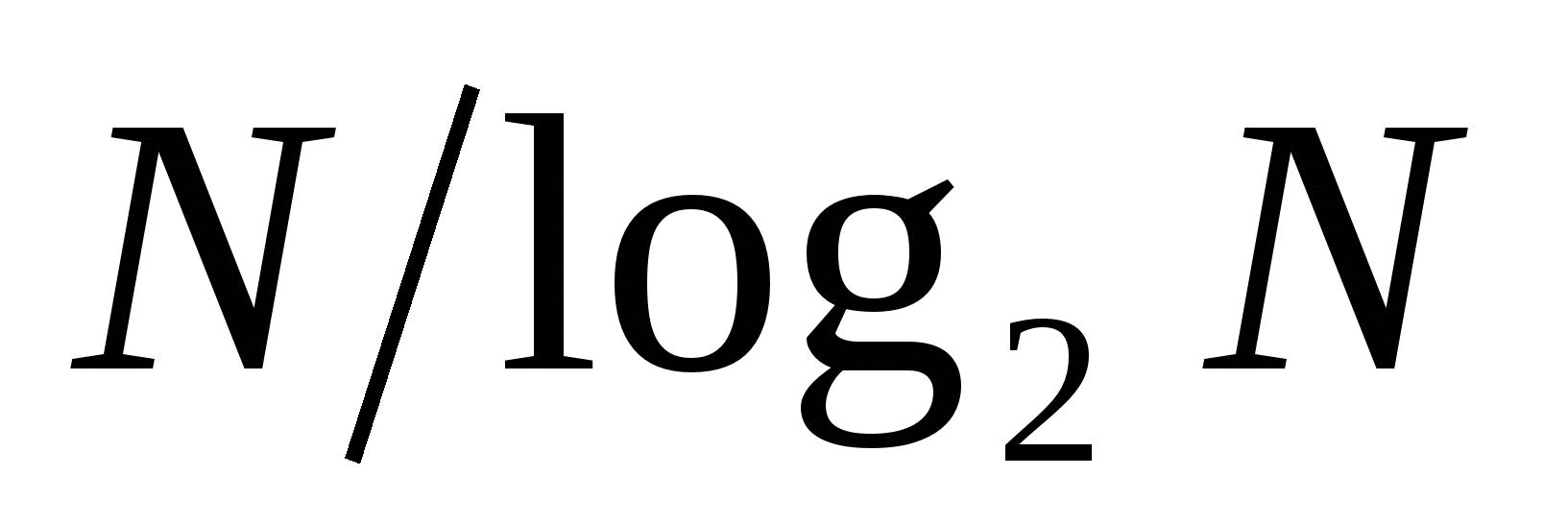раз эффективнее.
Следует отметить, что БПФ дает существенный выигрыш при вычислениях всех гармоник, но если нужны только некоторые гармоники, то можно использовать ДПФ.
Оценим время выполнения БПФ, положив производительность ПК равной тактовой частоте 1000МГц, т.е. 10⁹ опер./сек. Пусть 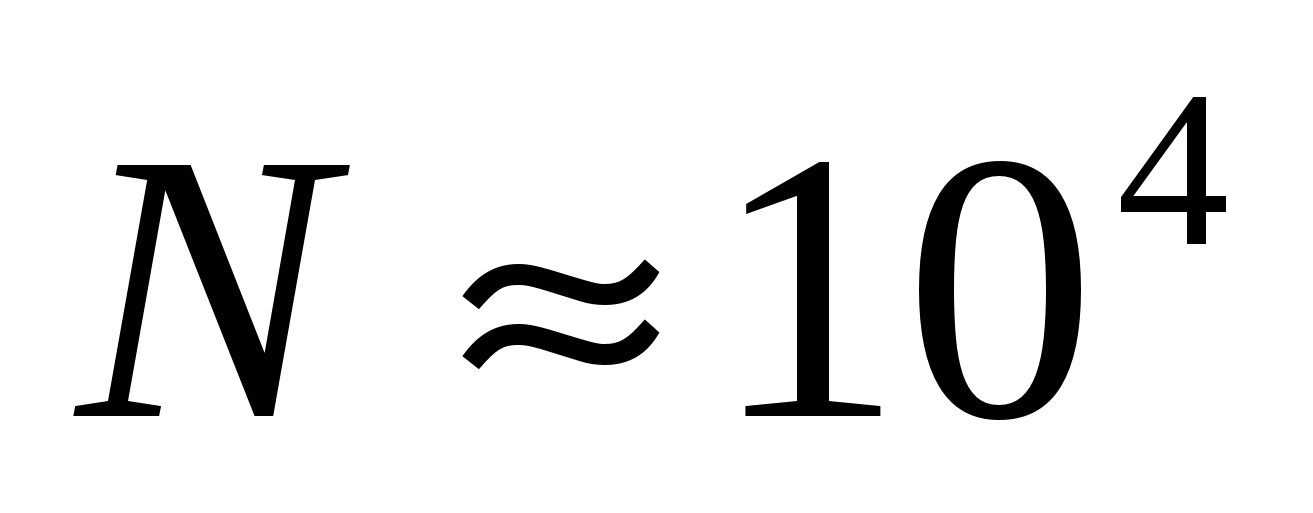, а количество операций 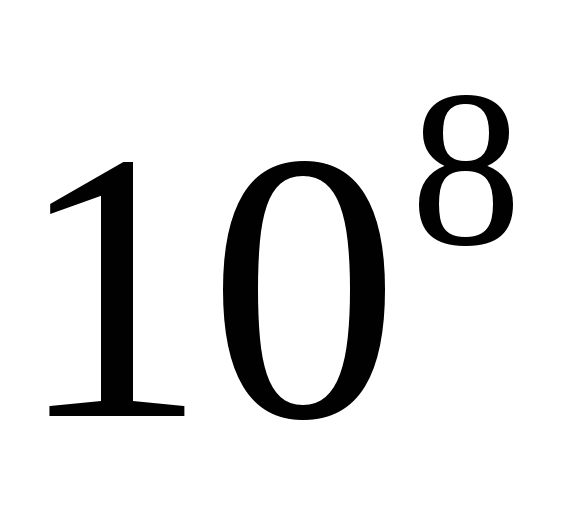и при этом учитываем, что вычисление комплексной exp(ihks) и комплексное умножение соответствуют нескольким десяткам машинных операций. В таблице 2.2 приведены оценки времени выполнения БПФ, а также количества телевизионных строк и пути ракеты за это время.
Таблица 2.2

	ДПФ	БПФ ПК	Специальный процессор для БПФ
Операции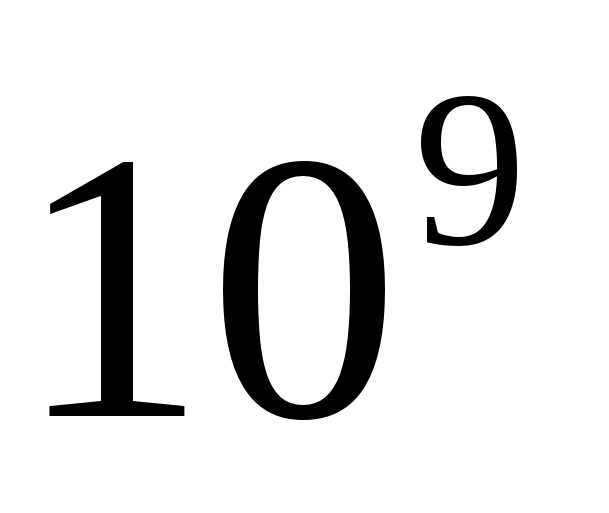
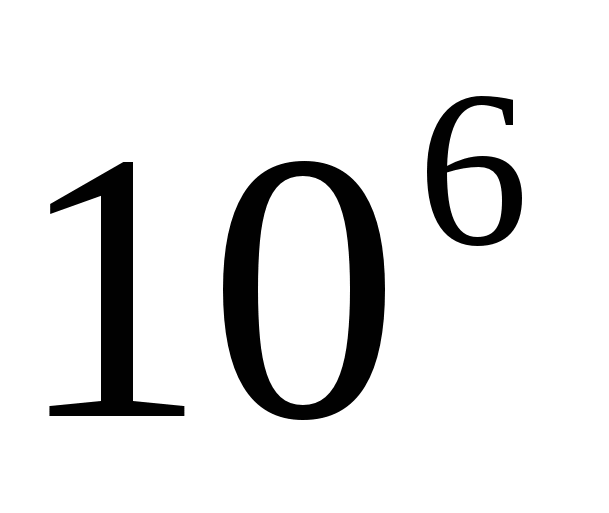
Время выполнения	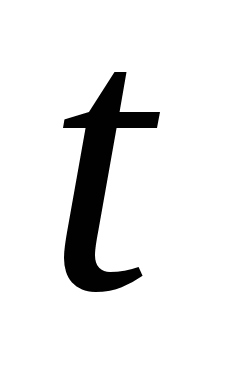10 сек =	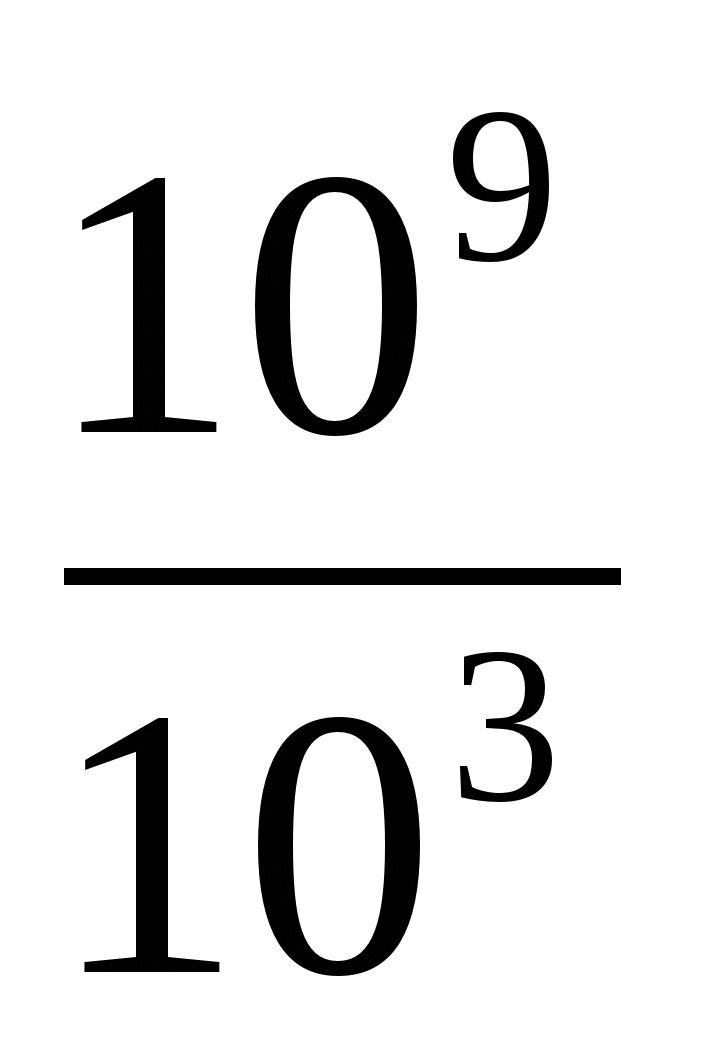10 мсек =	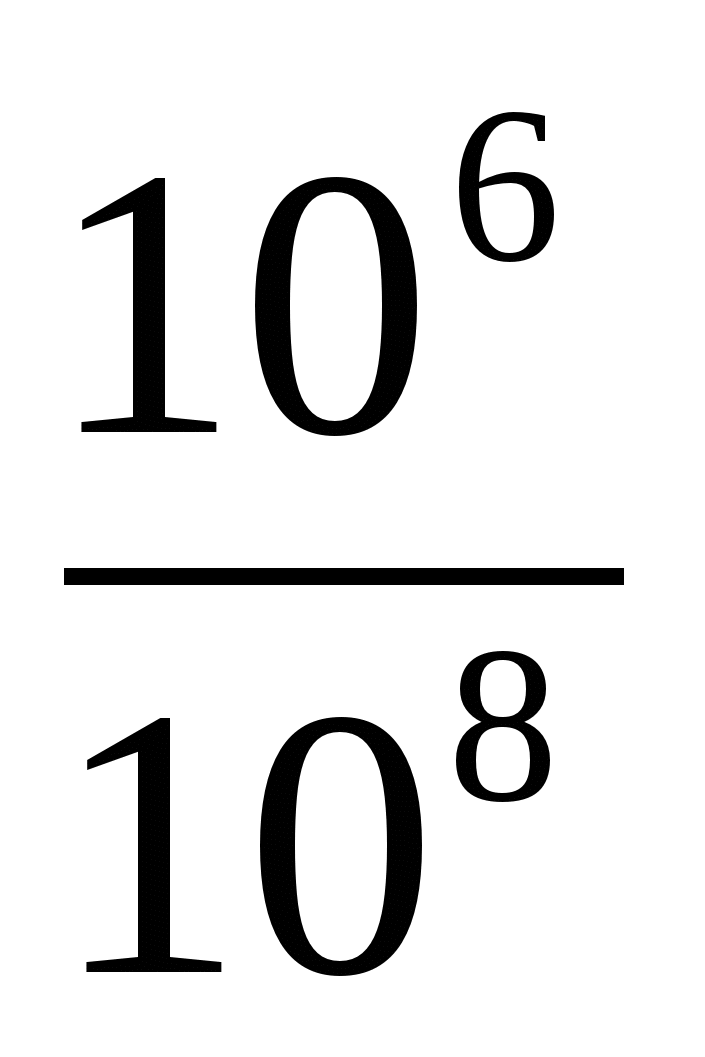1мсек
Телевизионных строк за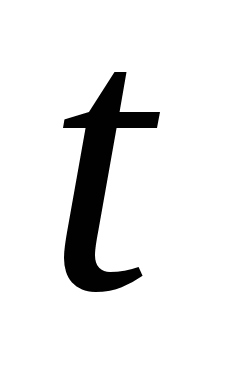
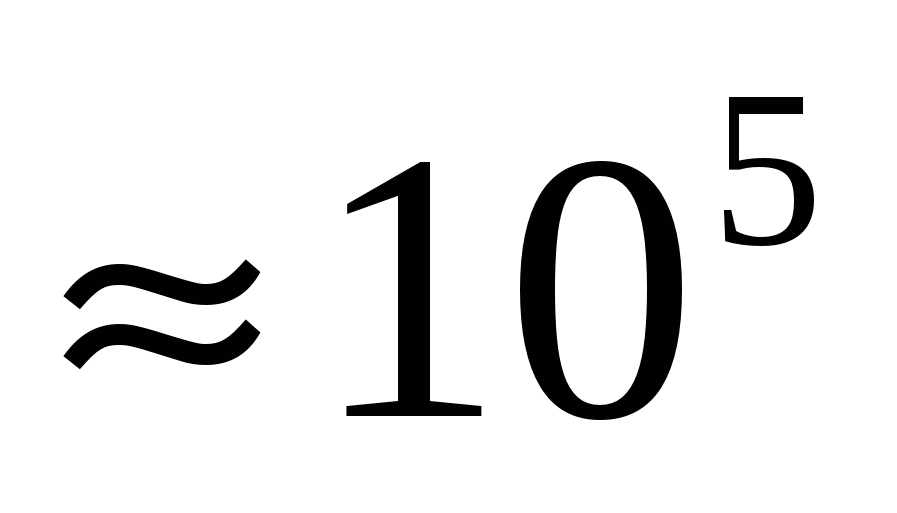
Путь ракеты за	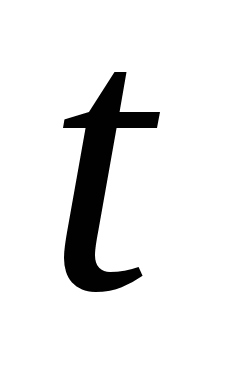10 км	10	1м

Таблица показывает, что БПФ можно использовать при цифровой обработке сигналов для практических задач.

ВЕЙВЛЕТ АНАЛИЗ

Основные понятия

Вейвлетное преобразование сигналов является обобщением спектрального

анализа, типичный представитель которого – классическое преобразование Фурье. Термин "вейвлет" (wavelet) в переводе с английского означает "маленькая (короткая) волна". Вейвлеты – это обобщенное название семейств математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени. Вейвлет-преобразования рассматривают анализируемые временные функции в терминах колебаний, локализованных по времени и частоте. Как правило, вейвлет-преобразования (WT) подразделяют на дискретное (DWT) и непрерывное (CWT). DWT используется для преобразований и кодирования сигналов, CWT - для анализа сигналов. Вейвлет-преобразования в настоящее время принимаются на вооружение для огромного числа разнообразных применений, нередко заменяя обычное преобразование Фурье. Это наблюдается во многих областях, включая молекулярную динамику, квантовую механику, астрофизику, геофизику, оптику, компьютерную графику и обработку изображений, анализ ДНК, исследования белков, исследования климата, общую обработку сигналов и распознавание речи.

Вейвлетный анализ представляет собой особый тип линейного преобразования

сигналов и физических данных. Базис собственных функций, по которому проводится вейвлетное разложение сигналов, обладает многими специфическими свойствами и возможностями. Вейвлетные функции базиса позволяют сконцентрировать внимание на тех или иных локальных особенностях анализируемых процессов, которые не могут быть выявлены с помощью традиционных преобразований Фурье и Лапласа. К таким процессам в геофизике относятся поля различных физических параметров природных сред. В первую очередь это касается полей температуры, давления, профилей сейсмических трасс и других физических величин. Вейвлеты имеют вид коротких волновых пакетов с нулевым средним значением, локализованных по оси аргументов (независимых переменных), инвариантных к сдвигу и линейных к операции масштабирования (сжатия/растяжения). По локализации во временном и частотном представлении вейвлеты занимают промежуточное положение между гармоническими функциями, локализованными по частоте, и функцией Дирака, локализованной во времени.

Теория вейвлетов не является фундаментальной физической теорией, но она дает удобный и эффективный инструмент для решения многих практических задач. Основная область применения вейвлетных преобразований – анализ и обработка сигналов и функций, нестационарных во времени или неоднородных в пространтве, когда результаты анализа должны содержать не только частотную характеристику сигнала (распределение энергии сигнала по частотным составляющим), но и сведения о локальных координатах, на которых проявляют себя те или иные группы частотных составляющих или на которых происходят быстрые изменения частотных составляющих сигнала. По сравнению с разложением сигналов на ряды Фурье вейвлеты способны с гораздо более высокой точностью представлять локальные особенности сигналов, вплоть до разрывов 1-го рода (скачков). В отличие от преобразований Фурье, вейвлет-преобразование одномерных сигналов обеспечивает двумерную развертку, при этом частота и координата рассматриваются как независимые переменные, что дает возможность анализа сигналов сразу в двух простран-ствах.

Одна из главных и особенно плодотворных идей вейвлетного представления сигналов на различных уровнях декомпозиции (разложения) заключается в разделении функций приближения к сигналу на две группы: аппроксимирующую – грубую, с достаточно медленной временной динамикой изменений, и детализирующую - с локальной и быстрой динамикой изменений на фоне плавной динамики, с последующим их дроблением и детализацией на других уровнях декомпозиции сигналов. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами.