Принцип вейвлет-преобразования

Гармонические базисные функции преобразования Фурье предельно локали-

зованы в частотной области (до импульсных функций Дирака при 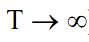) и не локализованы во временной (определены во всем временном интервале от 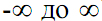). Их противоположностью являются импульсные базисные функции типа импульсов Кронекера, которые предельно локализованы во временной области и "размыты" по всему частотному диапазону. Вейвлеты по локализации в этих двух представлениях можно рассматривать как функции, занимающие промежуточное положение между гармоническими и импульсными функциями. Они должны быть локализованными как во временной, так и в частотной области представления. Однако при проектировании таких функций мы неминуемо столкнемся с принципом неопределенности, связывающим эффективные значения длительности функций и ширины их спектра. Чем точнее мы будем осуществлять локализацию временного положения функции, тем шире будет становиться ее спектр, и наоборот, что наглядно видно на рис. 3.5.

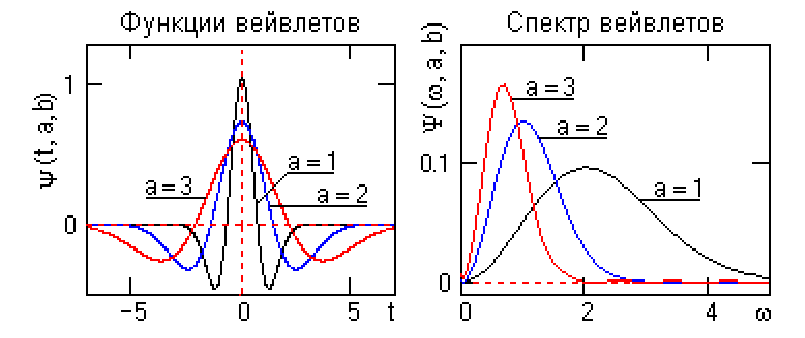
Рисунок 16.5 – Спектры функции

Отличительной особенностью вейвлет-анализа является то, что в нем можно использовать семейства функций, реализующих различные варианты соотношения неопределенности. Соответственно, исследователь имеет возможность гибкого вы-бора между ними и применения тех вейвлетных функций, которые наиболее эффективно решают поставленные задачи.

Вейвлетный базис пространства L² 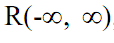, целесообразно конструировать из финитных функций, принадлежащих этому же пространству, которые должны стремиться к нулю на бесконечности. Чем быстрее эти функции стремятся к нулю, тем удобнее использовать их в качестве базиса преобразования при анализе ре-

альных сигналов. Допустим, что такой функцией является psi - функция 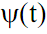, равная нулю за пределами некоторого конечного интервала и имеющая нулевое среднее значение по интервалу задания. Последнее необходимо для задания локализации спектра вейвлета в частотной области. На основе этой функции сконструируем базис в пространстве L² (R) с помощью масштабных преобразований независимой переменной.

Функция изменения частотной независимой переменной в спектральном пред-

ставлении сигналов отображается во временном представлении растяжени-

ем/сжатием сигнала. Для вейвлетного базиса это можно выполнить функцией типа

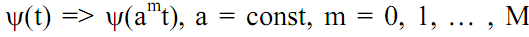, т.е. путем линейной операции растяжения/сжатия, обеспечивающей самоподобие функции на разных масштабах представления. Однако локальность функции на временной оси требует дополнительной независимой переменной последовательных сдвигов функции вдоль оси, типа 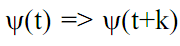, для перекрытия всей числовой оси пространства 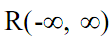. C учетом обеих условий одновременно структура базисной функции может быть принята следующей:

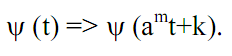(3.10)

Для упрощения дальнейших выкладок значения переменных m и k примем це-

лочисленными. При приведении функции (3.10) к единичной норме, получаем:

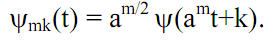(3.11)

Если для семейства функций 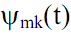выполняется условие ортогональности:

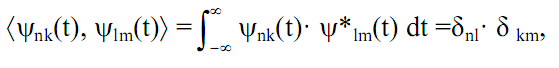(3.12)

то семейство 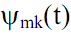можно использовать в качестве ортонормированного базиса пространства L² (R). Произвольную функцию этого пространства можно разложить в ряд по базису :

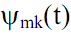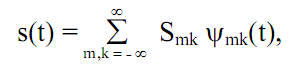(3.13)

где коэффициенты Smk – проекции сигнала на новый ортогональный базис

функций, как и в преобразовании Фурье, определяются скалярным произведением

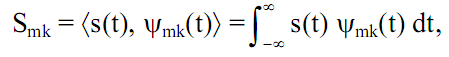(3.14)

при этом ряд равномерно сходиться:

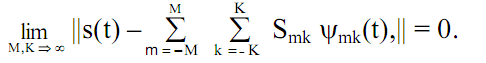При выполнении этих условий базисная функция преобразования 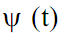называется ортогональным вейвлетом.

Простейшим примером ортогональной системы функций такого типа являются функции Хаара. Базисная функция Хаара определяется соотношением

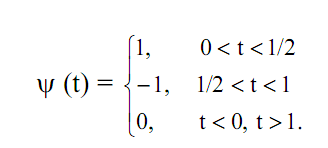( 16.15)

Легко проверить, что при а = 2, m = 0, 1, 2, ..., k = 0, 1,2, … две любые функции, полученные с помощью этого базисного вейвлета путем масштабных преобразований и переносов, имеют единичную норму и ортогональны. На рис. 3.6 приведены примеры функций для первых трех значений m и b при различных их комбинациях, где ортогональность функций видна наглядно.

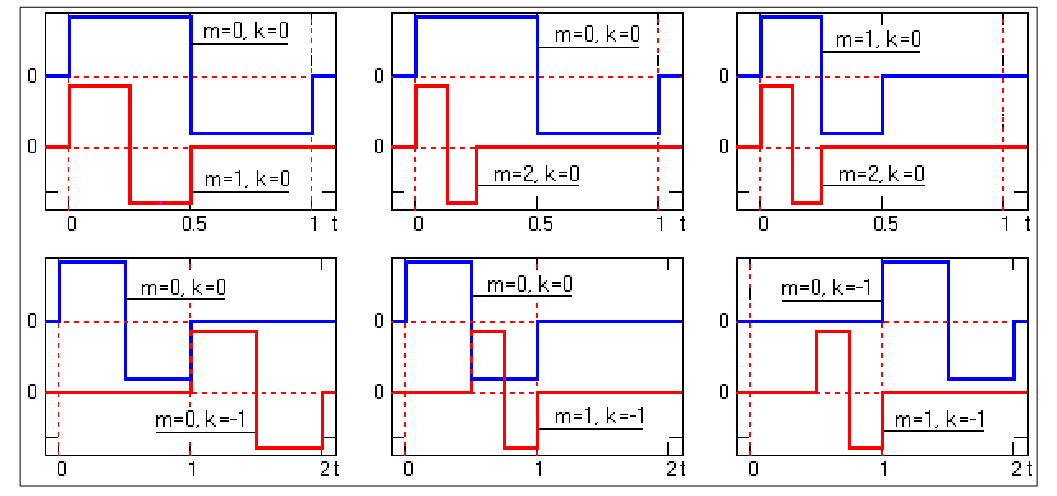
Рисунок 3.6 – Функции Хаара

Вейвлетный спектр

Вейвлетный спектр, в отличие от преобразования Фурье, является двумерным

и определяет двумерную поверхность в пространстве переменных m и k. При гра-

фическом представлении параметр растяжения/сжатия спектра m откладывается по оси абсцисс, параметр локализации k по оси ординат – оси независимой переменной сигнала. Математику процесса вейвлетного разложения сигнала в упрощенной форме рассмотрим на примере разложения сигнала s(t) вейвлетом Хаара с тремя последовательными по масштабу m вейвлетными функциями с параметром а=2, при этом сам сигнал s(t) образуем суммированием этих же вейвлетных функций с одинаковой амплитудой с разным сдвигом от нуля, как это показано на рис. 3.7.

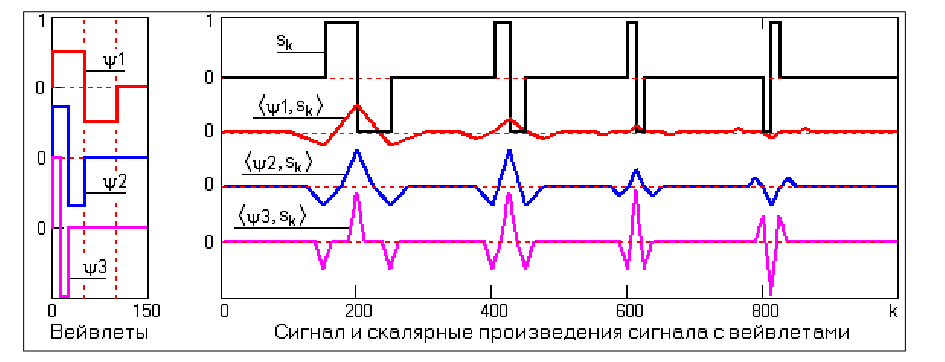
Рисунок 3.7 – Скалярные произведения сигнала с вейвлетами

Для начального значения масштабного коэффициента сжатия m определяется

функция вейвлета ( 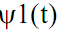на рис. 3.7), и вычисляется скалярное произведение сигнала с вейвлетом 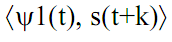с аргументом по сдвигу k. Для наглядности результаты вычисления скалярных произведений на рис. 3.7 построены по центрам вейвлетных функций (т.е. по аргументу k от нуля со сдвигом на половину длины вейвлетной функции). Как и следовало ожидать, максимальные значения скалярного произведения отмечаются там, где локализована эта же вейвлетная функция. После построения первой масштабной строки разложения, меняется масштаб вейвлетной функции ( 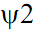на рис. 3.7) и выполняется вычисление второй масштабной строки спектра, и т.д.

Как видно на рис. 3.7, чем точнее локальная особенность сигнала совпадает с

соответствующей функцией вейвлета, тем эффективнее выделение этой особенности на соответствующей масштабной строке вейвлетного спектра. Можно видеть, что для сильно сжатого вейвлета Хаара характерной хорошо выделяемой локальной особенностью является скачок сигнала, причем выделяется не только скачок функции, но и направление скачка.

На рис. 3.8 приведен пример графического отображения вейвлетной поверхности реального физического процесса. Вид поверхности определяет изменения во времени спектральных компонент различного масштаба и называется частотно-временным спектром. Поверхность изображается на рисунках, как правило, в виде изолиний или условными цветами. Для расширения диапазона масштабов может применяться логарифмическая шкала.

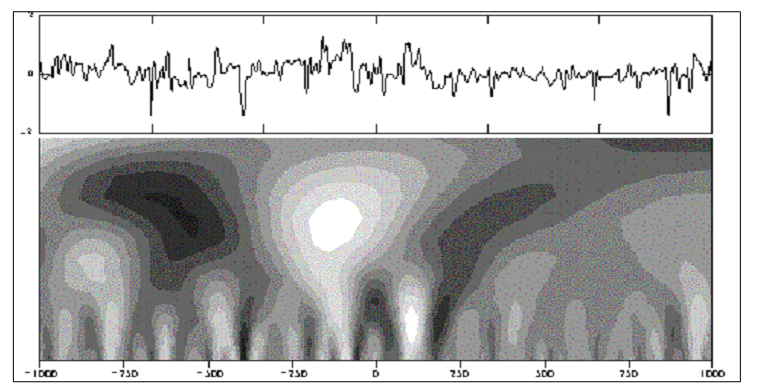
Рисунок 3.8 – Пример вейвлетного преобразования

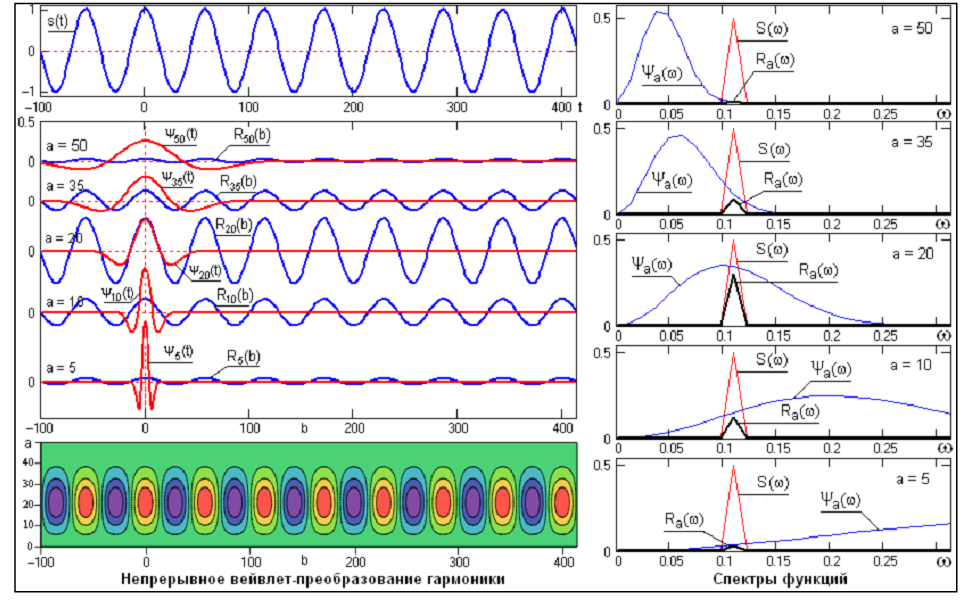
Рисунок 3.9 – Вейвлет-преобразование чистого гармонического сигнала