Преобразование Фурье

В основе спектрального анализа сигналов лежит интегральное преобразование

и ряды Фурье. Напомним некоторые математические определения.

В пространстве функций, заданных на конечном интервале (0,T), норма, как

числовая характеристика произвольной функции s(t), вычисляется как корень квадратный из скалярного произведения функции. Для комплексных функций, квадрат нормы (энергия сигнала) соответствует выражению:

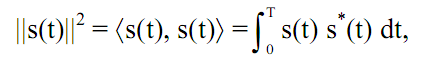(3.1)

где s*(t) – функция, комплексно сопряженная с s(t).

Если норма функции имеет конечное значение (интеграл сходится), то гово-

рят, что функция принадлежит пространству функций L²

[R], R=[0,T], интегрируемых с квадратом (пространство Гильберта), и имеет конечную энергию. В пространстве Гильберта на основе совокупности ортогональных функций с нулевым скалярным произведением

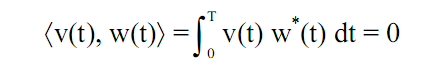
может быть создана система ортонормированных "осей" (базис пространства), при этом любой сигнал, принадлежащий этому пространству, может быть представлен в виде весовой суммы проекций сигнала на эти "оси" – базисных векторов. Значения проекций определяются скалярными произведениями сигнала с соответствующими функциями базисных "осей". Базис пространства может быть образован любой ортогональной системой функций. Наибольшее применение в спектральном анализе получила система комплексных экспоненциальных функций. Проекции сигнала на данный базис определяются выражением:

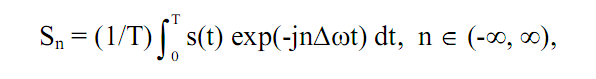(3.2)

где – частотный аргумент векторов. При известных выражениях базисных функций сигнал s(t) однозначно определяется совокупностью коэффициентов Sn и может быть абсолютно точно восстановлен (реконструирован) по этим коэффициентам:

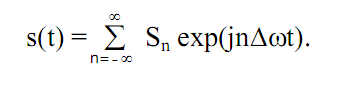(3.3)

Уравнения (3.2) и (3.3) называют прямым и обратным преобразованием

Фурье сигнала s(t). Любая функция гильбертова пространства может быть представлена в виде комплексного ряда Фурье (3.3), который называют спектром сигнала или его Фурье-образом.

Ряд Фурье ограничивается определенным количеством членов N, что означает

аппроксимацию с определенной погрешностью бесконечномерного сигнала N – мерной системой базисных функций спектра сигнала. Ряд Фурье равномерно сходится к s(t):

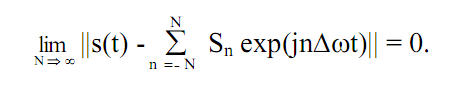(3.4)

Таким образом, ряд Фурье - это разложение сигнала s(t) по базису простран-

ства L² (0,T) ортонормированных гармонических функций exp(jnt) с изменением частоты, кратным частоте первой гармоники 1=. Отсюда следует, что ортонормированный базис пространства L² (0,T) построен из одной функции 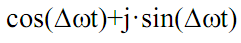с помощью масштабного преобразования независимой переменной.

Для коэффициентов ряда Фурье справедливо равенство Парсеваля сохранения

энергии сигнала в различных представлениях:

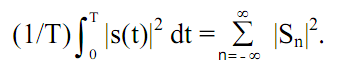(3.5)

Разложение в ряд Фурье произвольной функции y(t) корректно, если функция

y(t) принадлежит этому же пространству L2(0,T), т.е. квадратично интегрируема с конечной энергией:

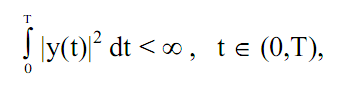(3.6)

при этом она может быть периодически расширена и определена на всей временной оси пространства 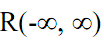так, что

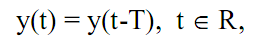
при условии сохранения конечности энергии в пространстве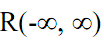

С позиций анализа произвольных сигналов и функций в частотной области и точного восстановления после преобразований можно отметить ряд недостатков разложения сигналов в ряды Фурье, которые привели к появлению оконного преобразования Фурье и стимулировали развитие вейвлетного преобразования. Основные из них:

- Ограниченная информативность анализа нестационарных сигналов и практи-

чески полное отсутствие возможностей анализа их особенностей (сингулярно-

стей), т.к. в частотной области происходит «размазывание» особенностей сиг-

налов (разрывов, ступенек, пиков и т.п.) по всему частотному диапазону спек-

тра.

- Гармонические базисные функции разложения не способны отображать пере-

пады сигналов с бесконечной крутизной типа прямоугольных импульсов, т.к.

для этого требуется бесконечно большое число членов ряда. При ограничении

числа членов ряда Фурье в окрестностях скачков и разрывов при восстановле-

нии сигнала возникают осцилляции (явление Гиббса).

- Преобразование Фурье отображает глобальные сведения о частотах исследуе-

мого сигнала и не дает представления о локальных свойствах сигнала при

быстрых временных изменениях его спектрального состава. Так, например,

преобразование Фурье не различает стационарный сигнал с суммой двух си-

нусоид от нестационарного сигнала с двумя последовательно следующими

синусоидами с теми же частотами, т.к. спектральные коэффициенты (3.2)

вычисляются интегрированием по всему интервалу задания сигнала. Преобра-

зование Фурье не имеет возможности анализировать частотные характеристи-

ки сигнала в произвольные моменты времени.