АНАЛОГОВОЕ И ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ.
2.1. Задача спектрального анализа и цифровая обработка сигналов.
Непрерывную или дискретную функцию 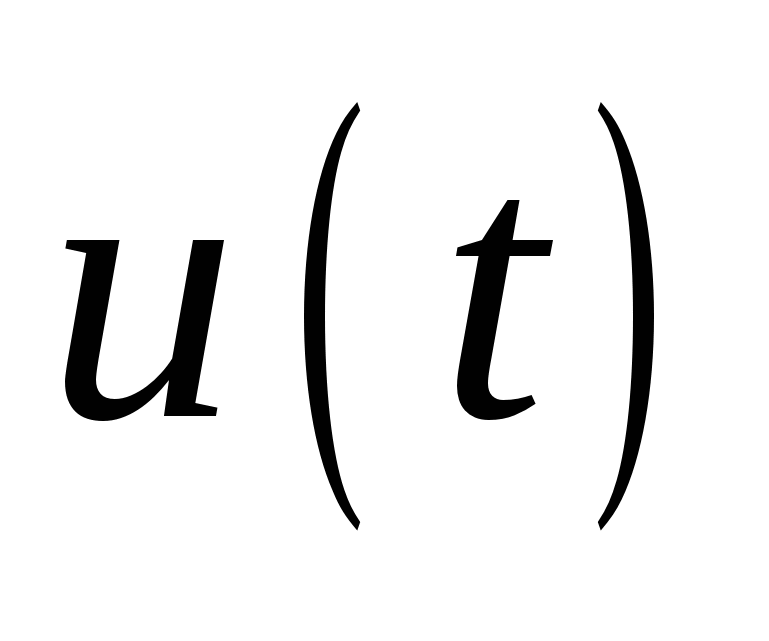 одного переменного
одного переменного 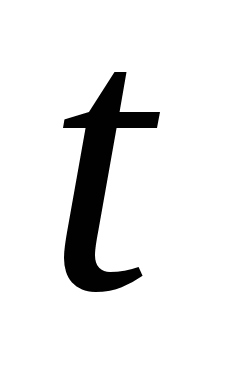 можно представить рядов Фурье по тригонометрическим функциям
можно представить рядов Фурье по тригонометрическим функциям 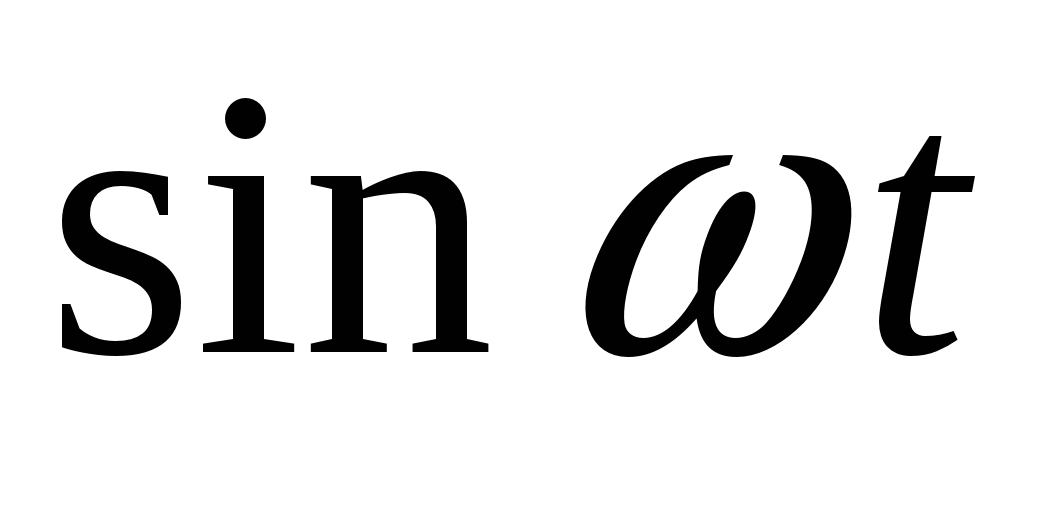 ,
, 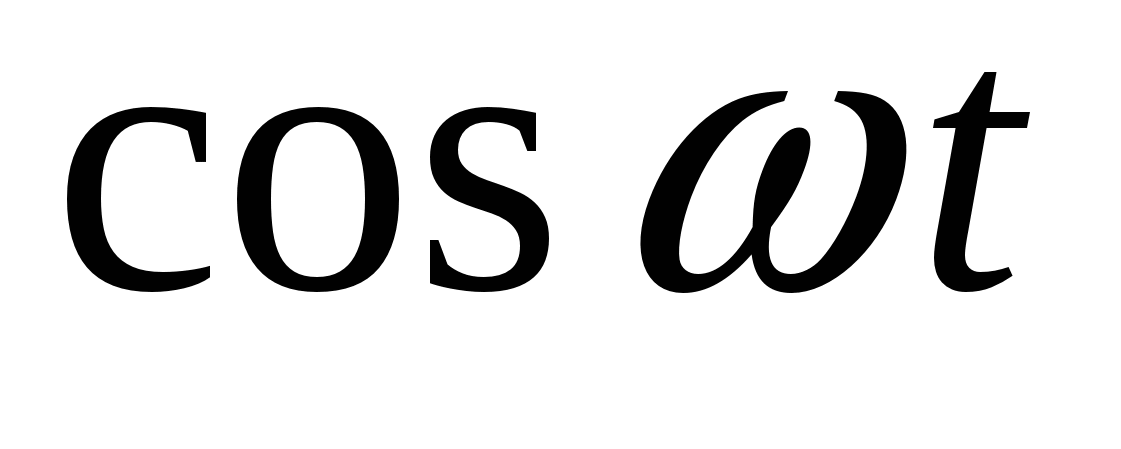 или интегралом Фурье от этих функций. Задача спектрального анализа состоит в определении спектра функции – кооффициентов ряда Фурье и спектральной плотности в интеграле Фурье в зависимости от частоты
или интегралом Фурье от этих функций. Задача спектрального анализа состоит в определении спектра функции – кооффициентов ряда Фурье и спектральной плотности в интеграле Фурье в зависимости от частоты 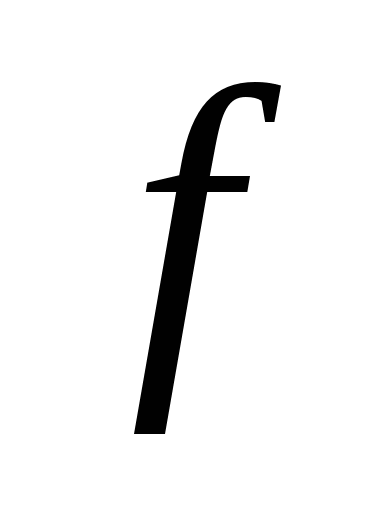 или круговой частоты
или круговой частоты 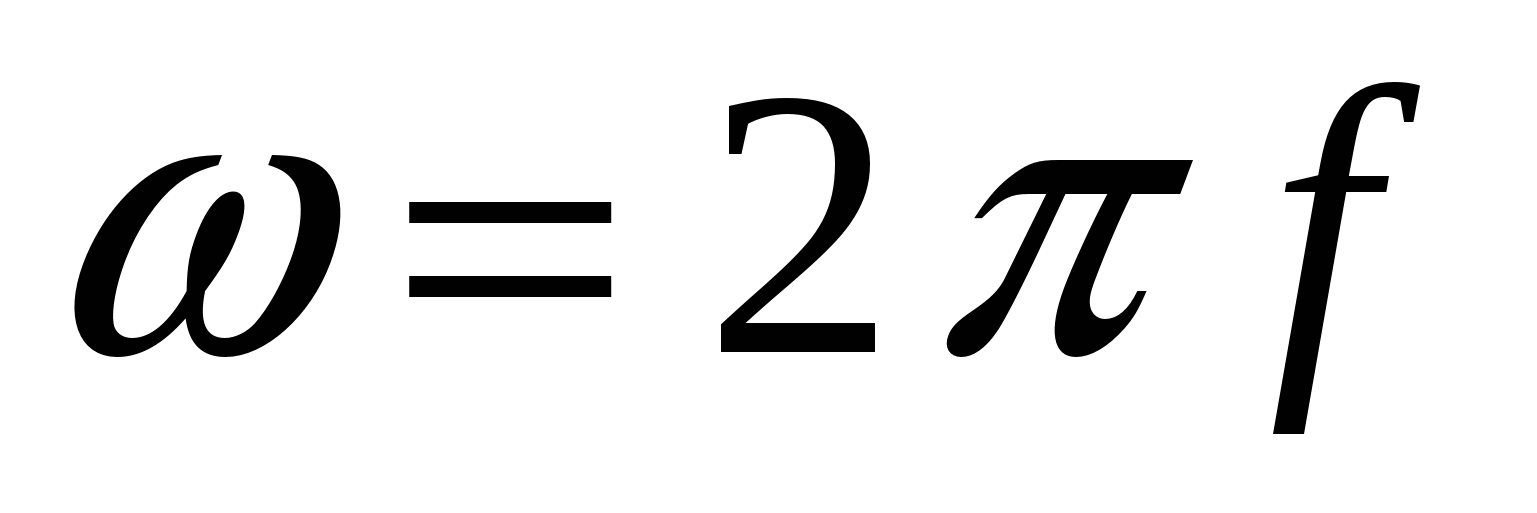 . Спектральный анализ сигналов имеет очень важное значение в радиоэлектронике, поэтому функцию
. Спектральный анализ сигналов имеет очень важное значение в радиоэлектронике, поэтому функцию 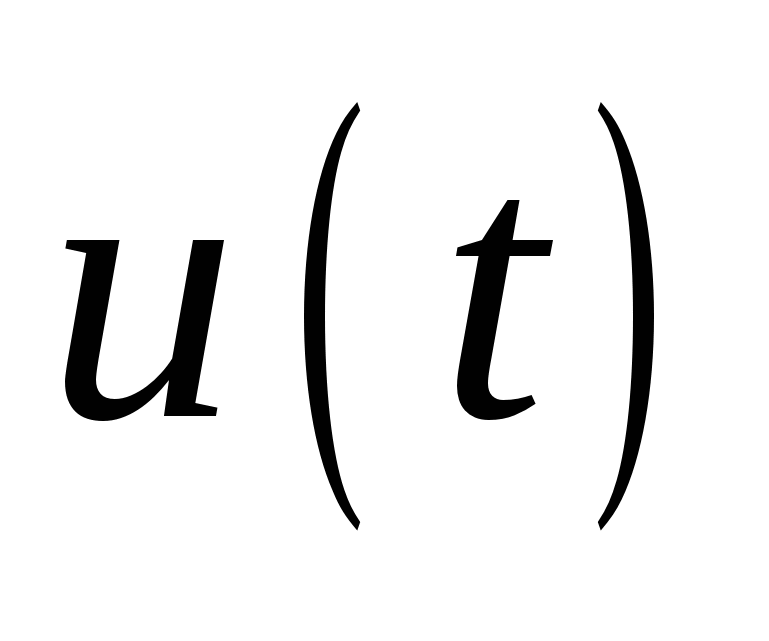 обычно рассматривают как сигнал, зависящей от времени
обычно рассматривают как сигнал, зависящей от времени 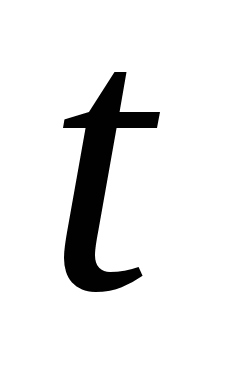 .
.
Цифровая обработка состоит из двух больших областей: спектрального анализа и цифровых фильтров. Обе области рассматривают цифровые сигналы, называемые также дискретными, которые представляются в виде дискретных функций времени 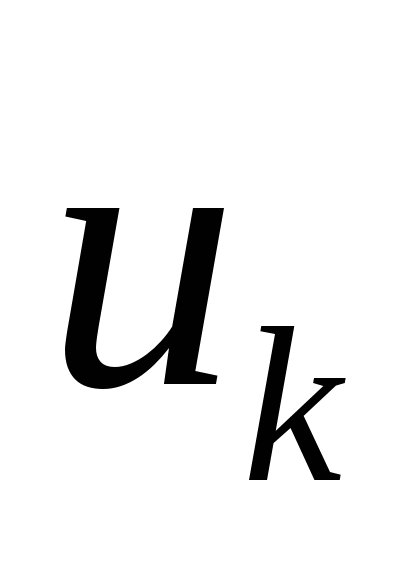 с постоянным шагом дискретизации
с постоянным шагом дискретизации  , т.е. время
, т.е. время 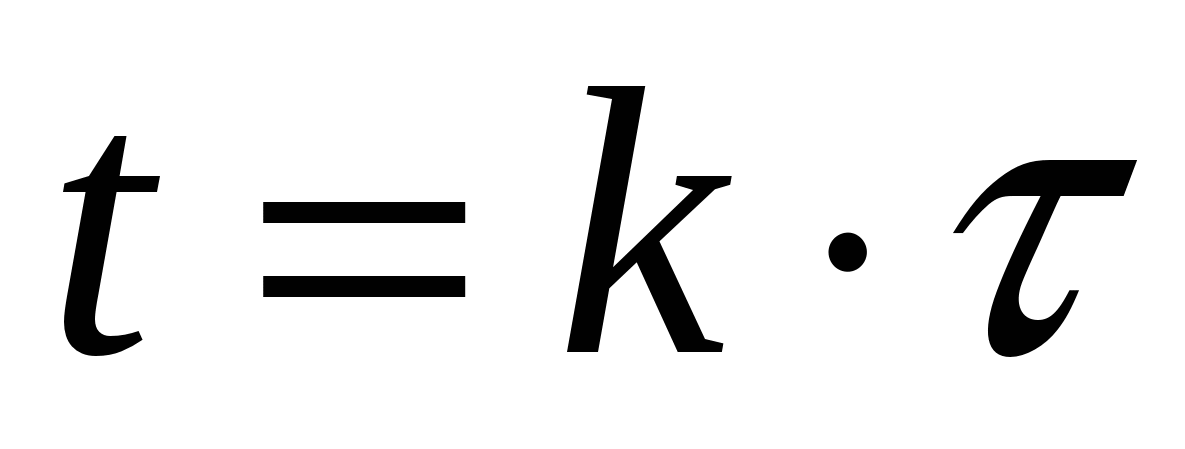 , где
, где 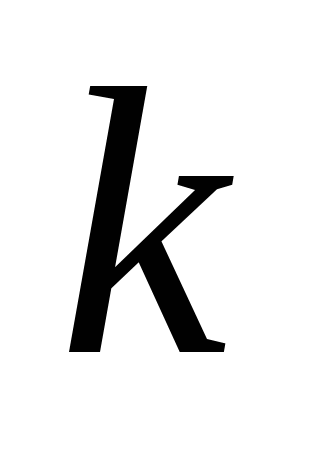 – номер отсчета . Цифровой сигнал получается при дискретизации аналогового сигнала
– номер отсчета . Цифровой сигнал получается при дискретизации аналогового сигнала 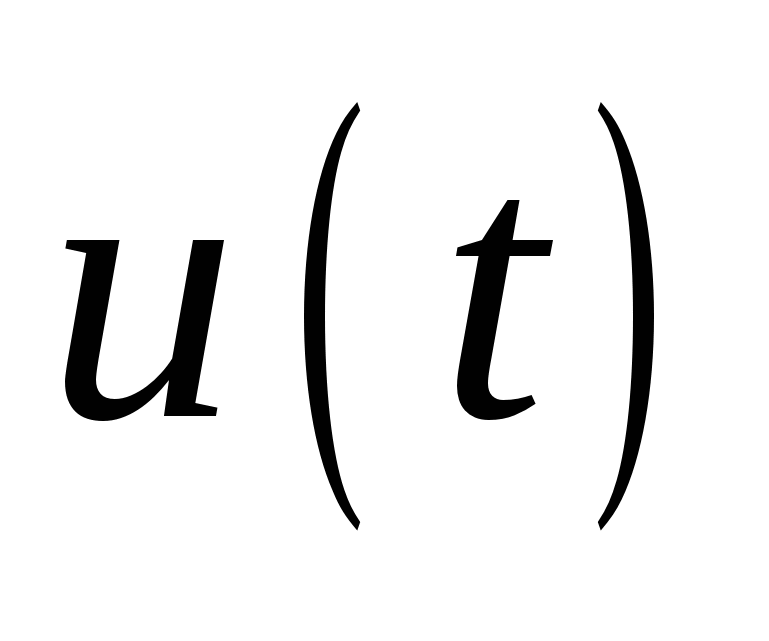 , представляемого непрерывной функцией времени.
, представляемого непрерывной функцией времени.
Алгоритмы цифровой обработки позволяют выполнять различные преобразования дискретных функций, причем можно преобразовывать как сами функции, так и их спектры.
Рассмотрим периодические и непериодические сигналы. В таблице 2.1 приводятся основные характеристики сигналов и их спектров, причем используются следующие обозначения:
Д=1 означает дискретный, Д=0 – аналоговый, П=1 означает периодический, П=0 – непериодический.
Таблица2.1.
Аналоговые и дискретные сигналы и их спектры
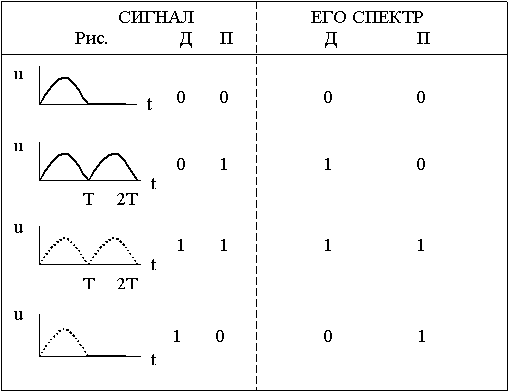
Дискретный непериодический сигнал (Д=1, П=0) при цифровой обработке обычно рассматривают как периодический (Д=1, П=1) с большими и физически разумными значениями периода 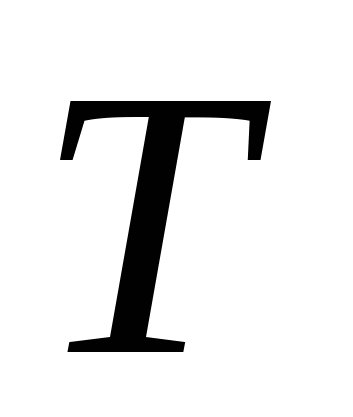 .
.
Период 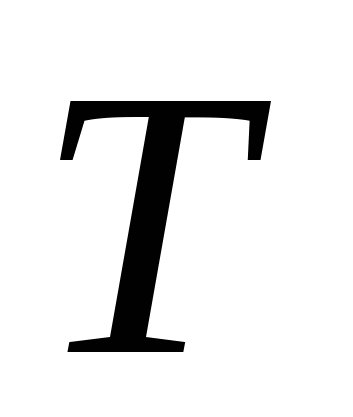 определяет разрешение в спектре, т.е. разность частот соседних составляющих равна
определяет разрешение в спектре, т.е. разность частот соседних составляющих равна 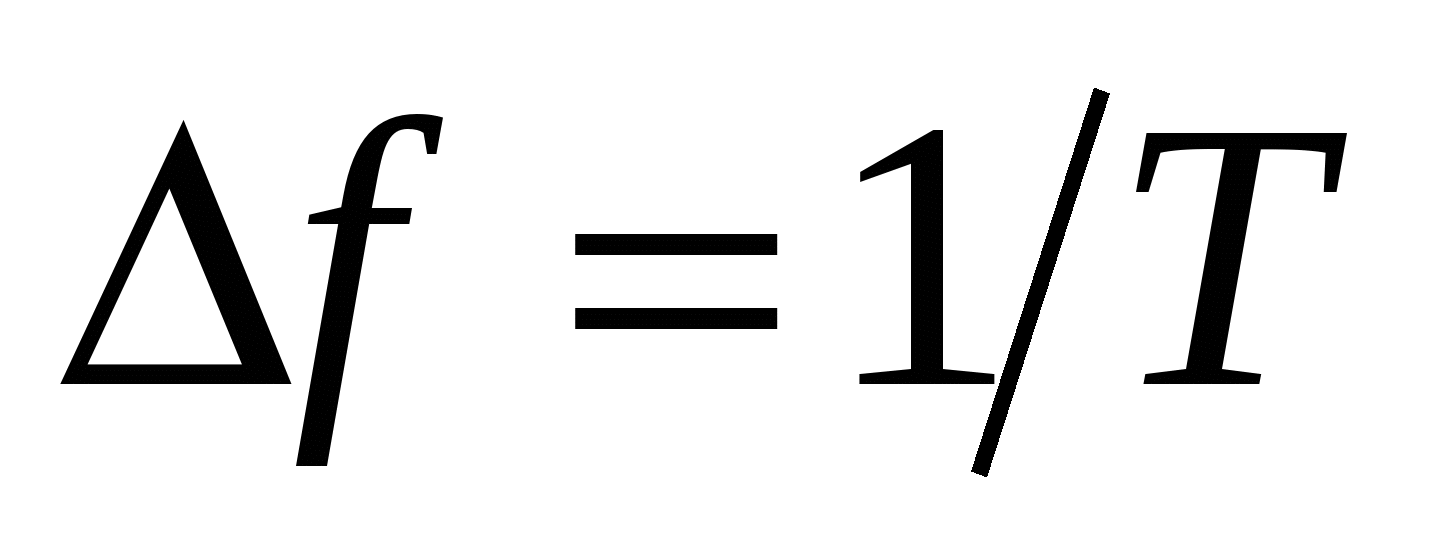 . Очевидно, что при
. Очевидно, что при  получаем
получаем 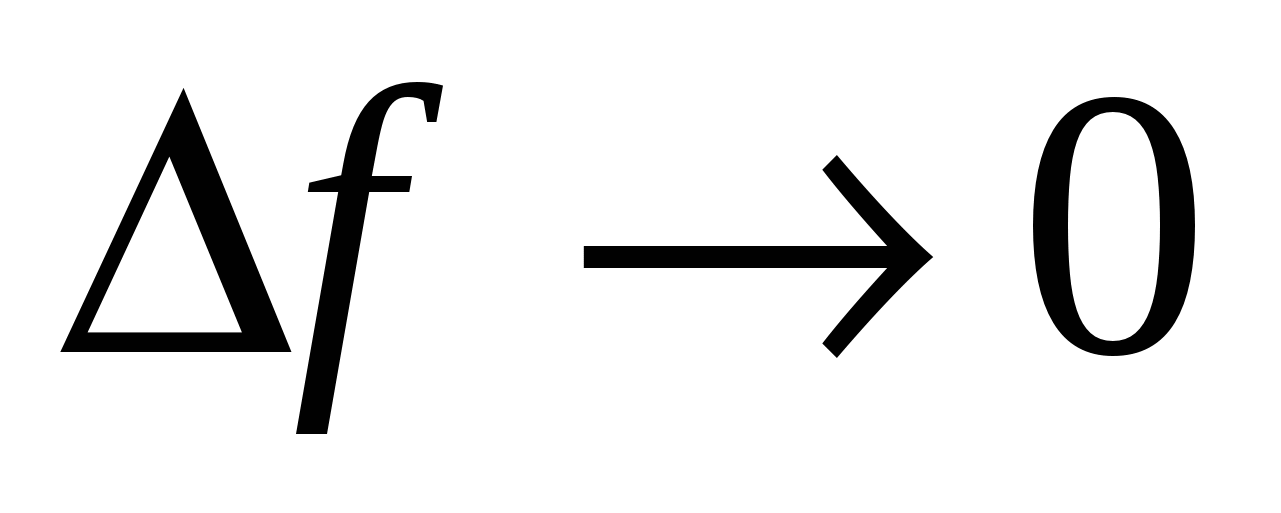 , т.е. сплошной спектр (Д=0).
, т.е. сплошной спектр (Д=0).
Количество составляющих в спектре дискретного сигнала определяется количеством отсчетов  на периоде
на периоде 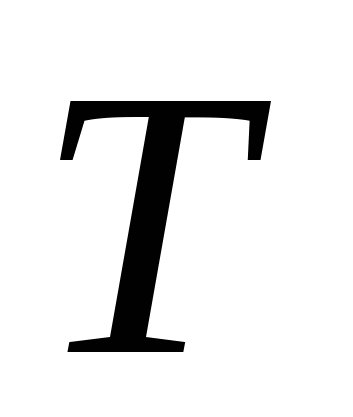 .
.
2.2. Аналоговое преобразование Фурье (АПФ).
АПФ – это преобразование Фурье для аналогового сигнала, представляемого непрырывной функцией 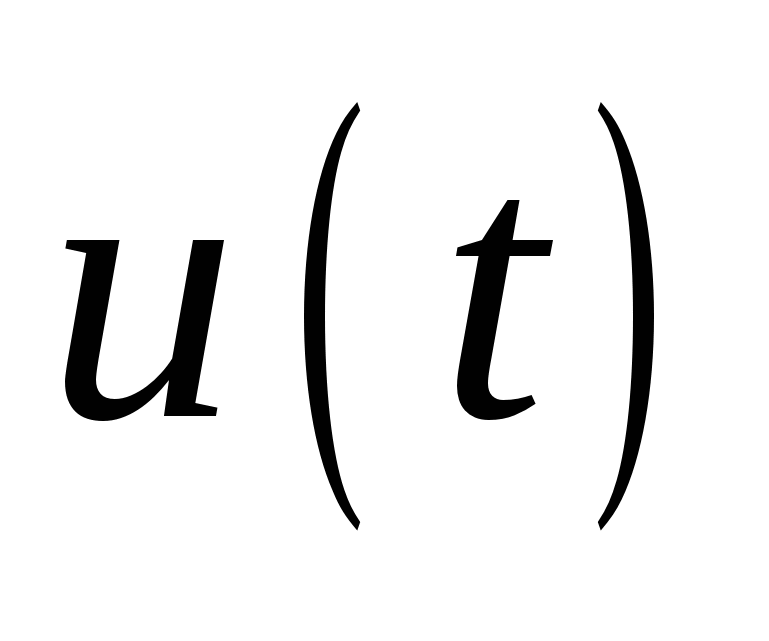 .
.
Переодическую функцию 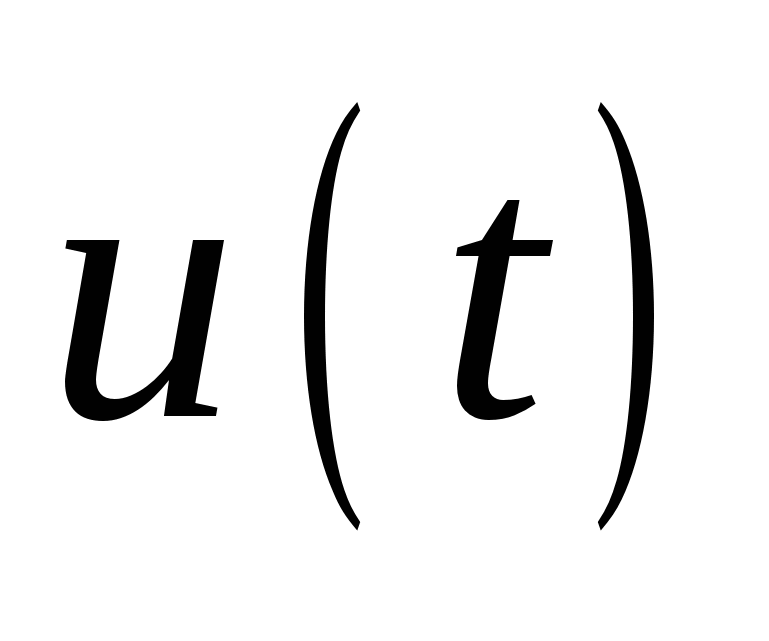 , имеющую период
, имеющую период 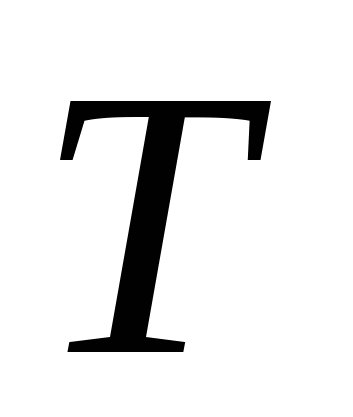 , можно представить рядом Фурье.
, можно представить рядом Фурье.
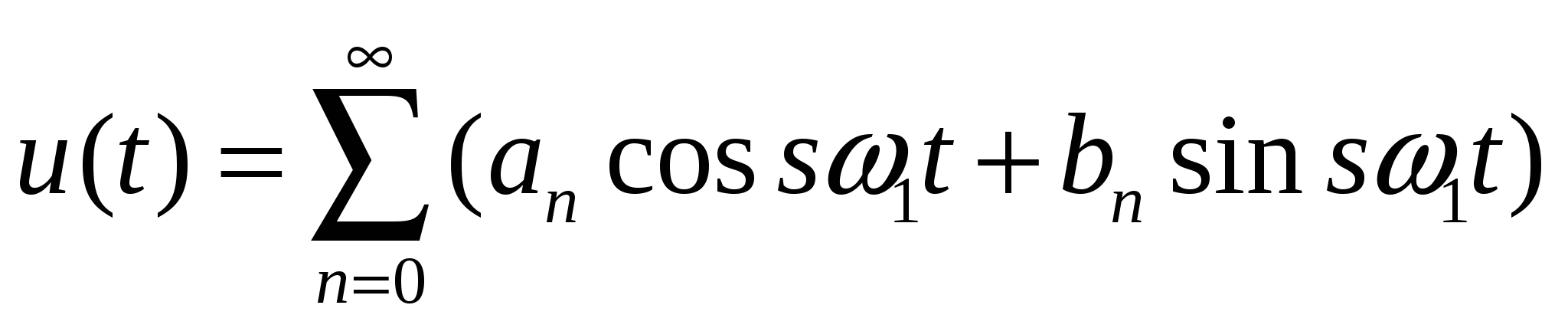 , ,
| (2.1) |
где 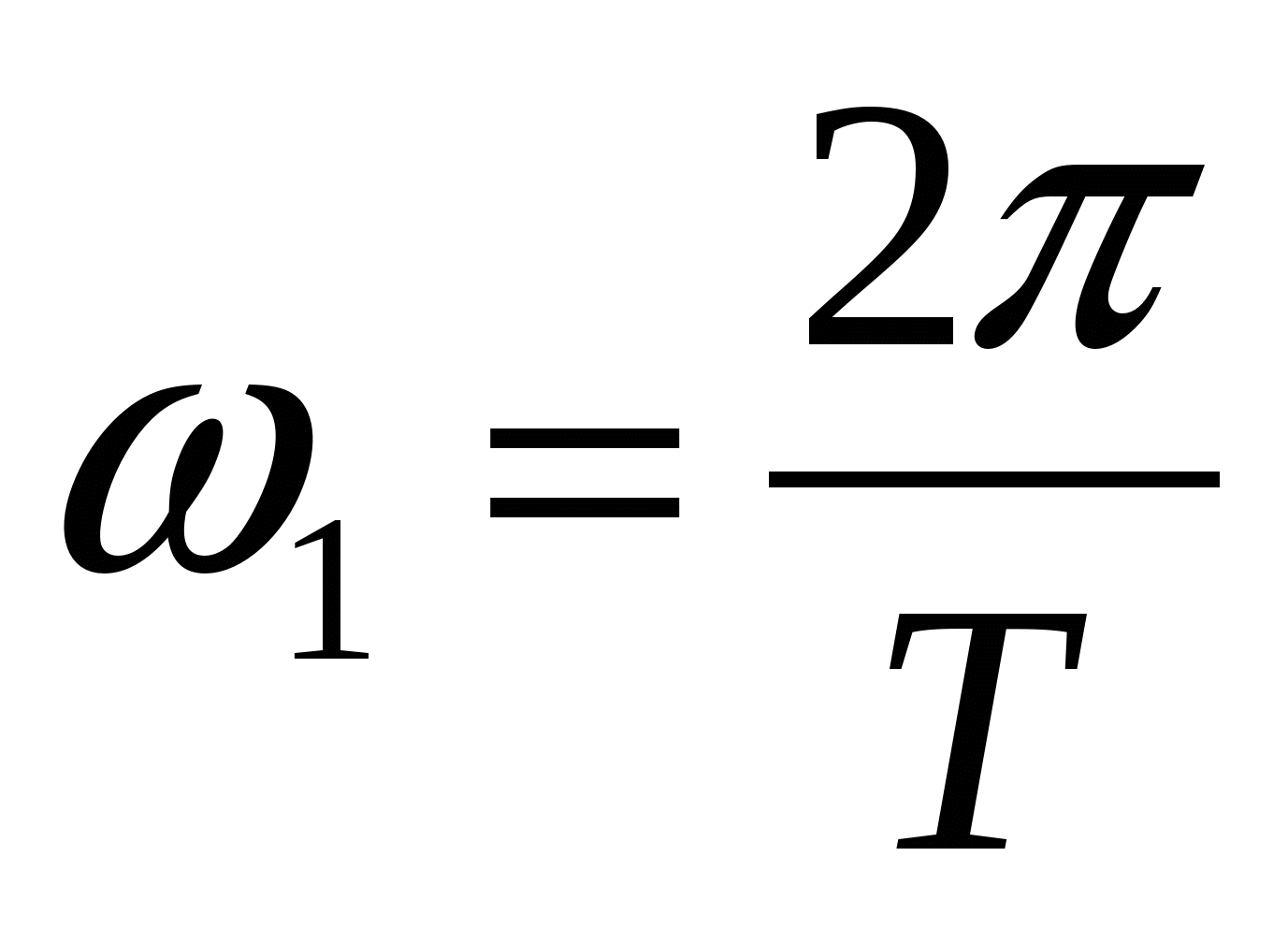 - основная круговая частота сигнала,
- основная круговая частота сигнала,
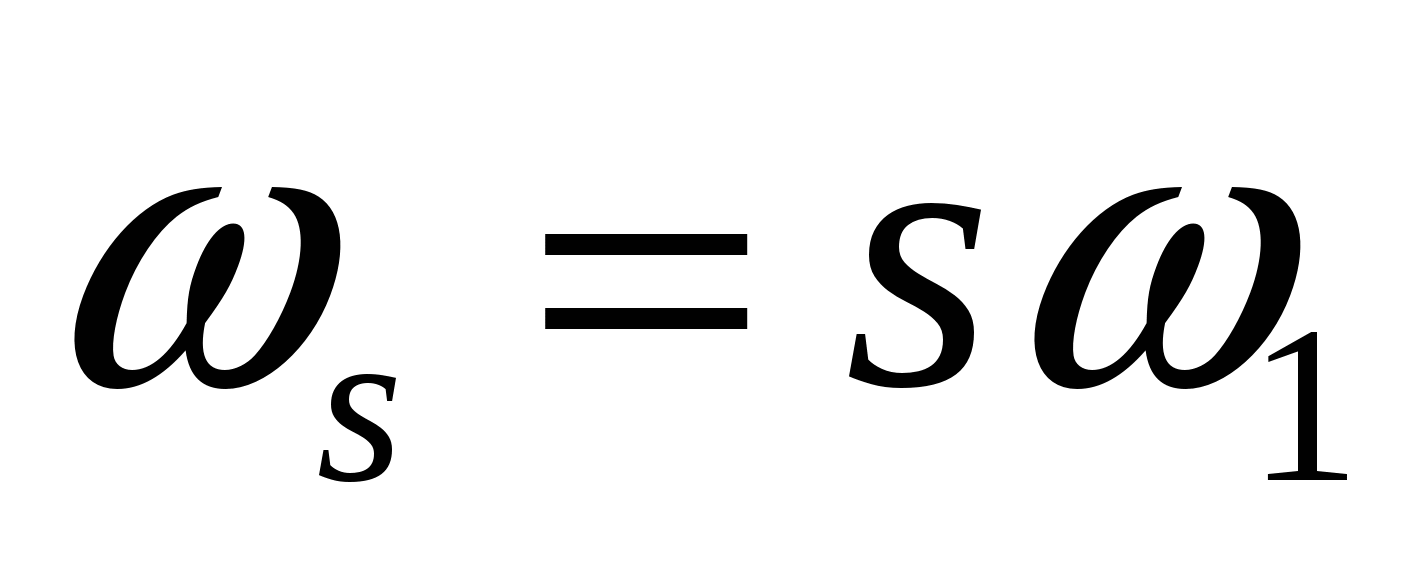 - круговая частота
- круговая частота 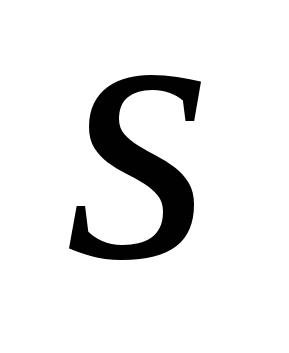 -й гармоники сигнала,
-й гармоники сигнала,
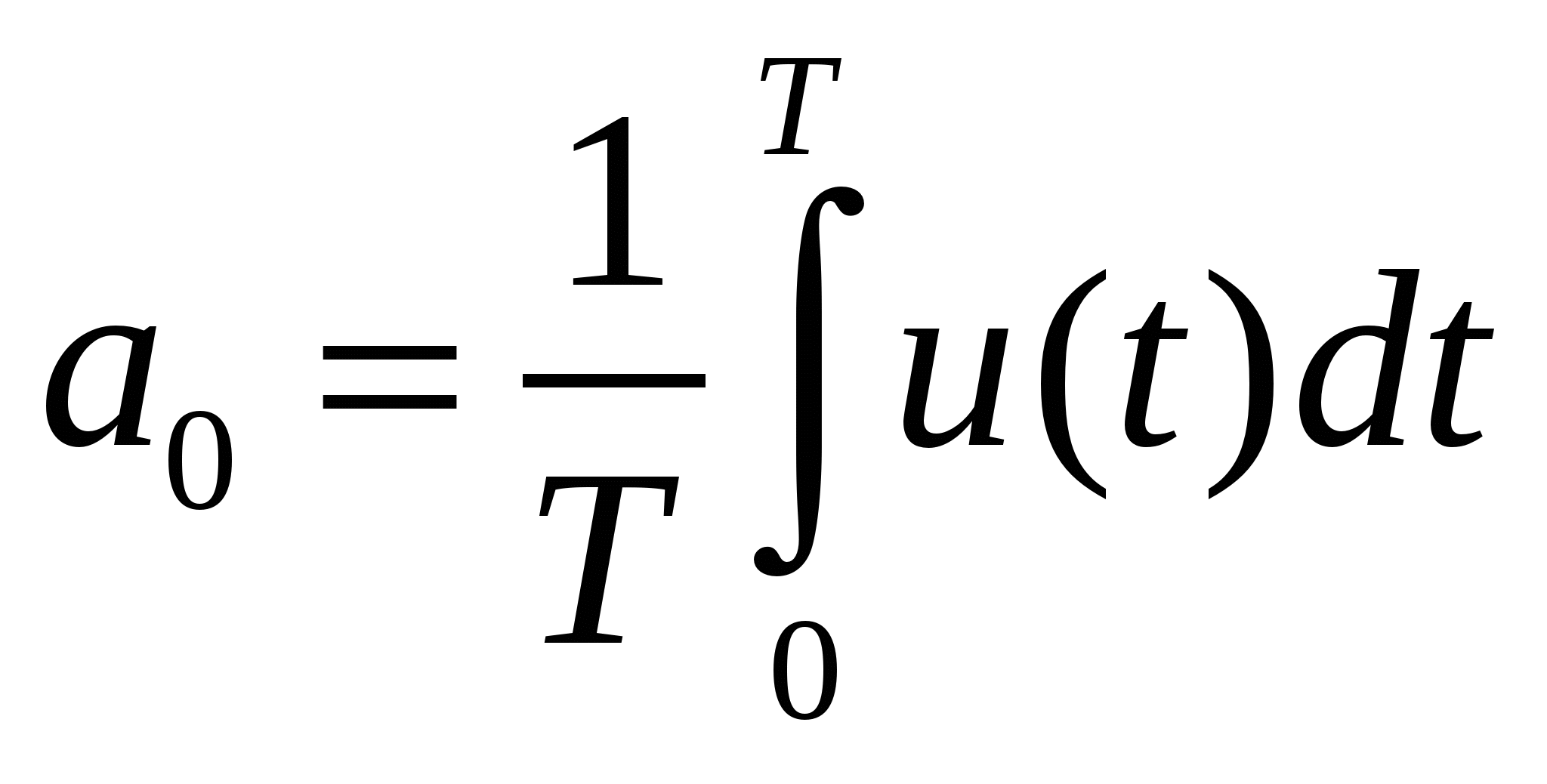
| (2.2) |
- среднее значение (постоянная состовляющая сигнала) сигнала,
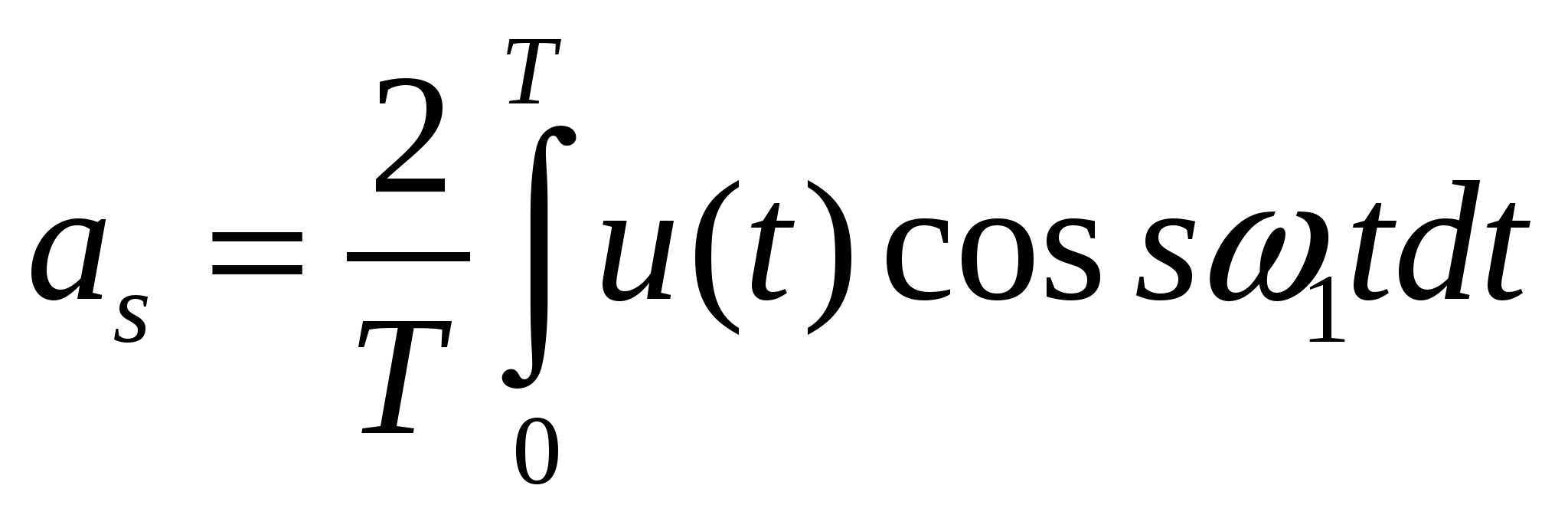
| (2.3) |
- косинусные коэффициенты сигнала,
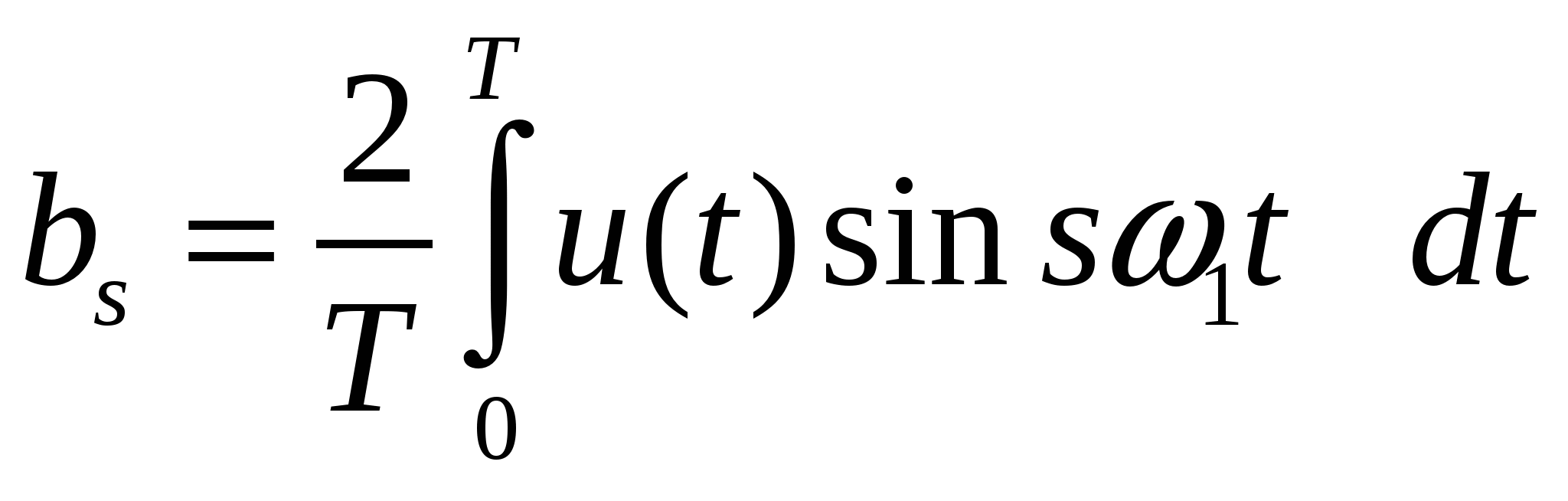
| (2.4) |
- синусные коэффициенты сигнала.
Ряд (11.1) можно переписать в виде
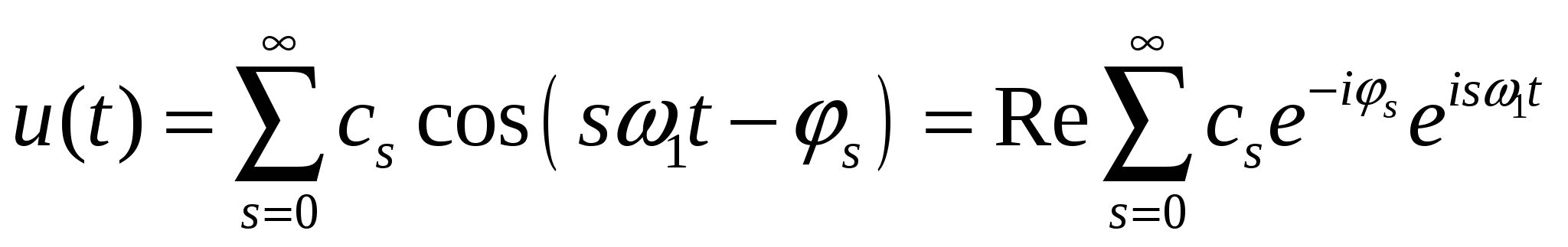
| (2.5) |
Здесь 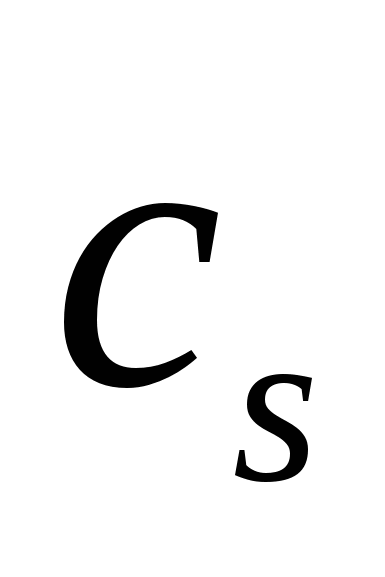 – амплитуда гармоники с номером
– амплитуда гармоники с номером 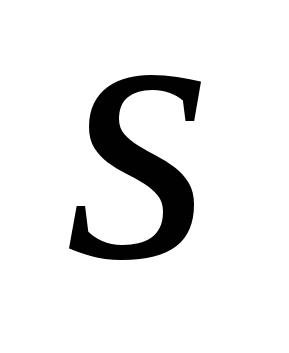 ,
,  – фаза той же гармоники. Значения
– фаза той же гармоники. Значения 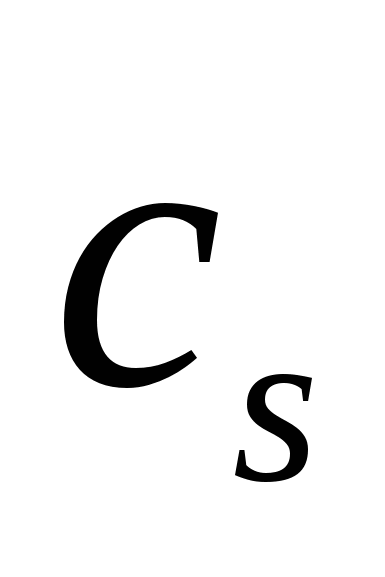 и
и  определяются по коэффициентам
определяются по коэффициентам 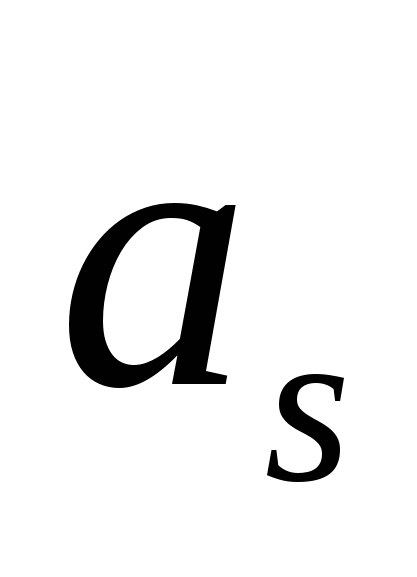 ,
, 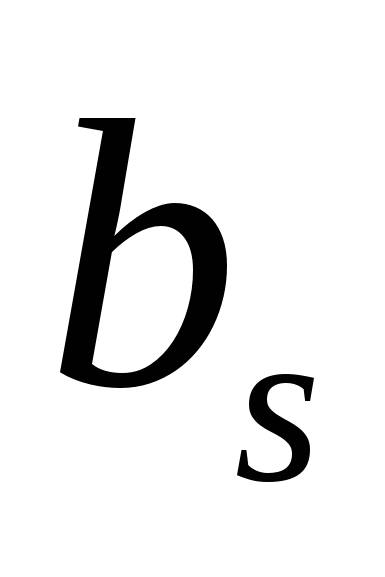 с помощью формул
с помощью формул
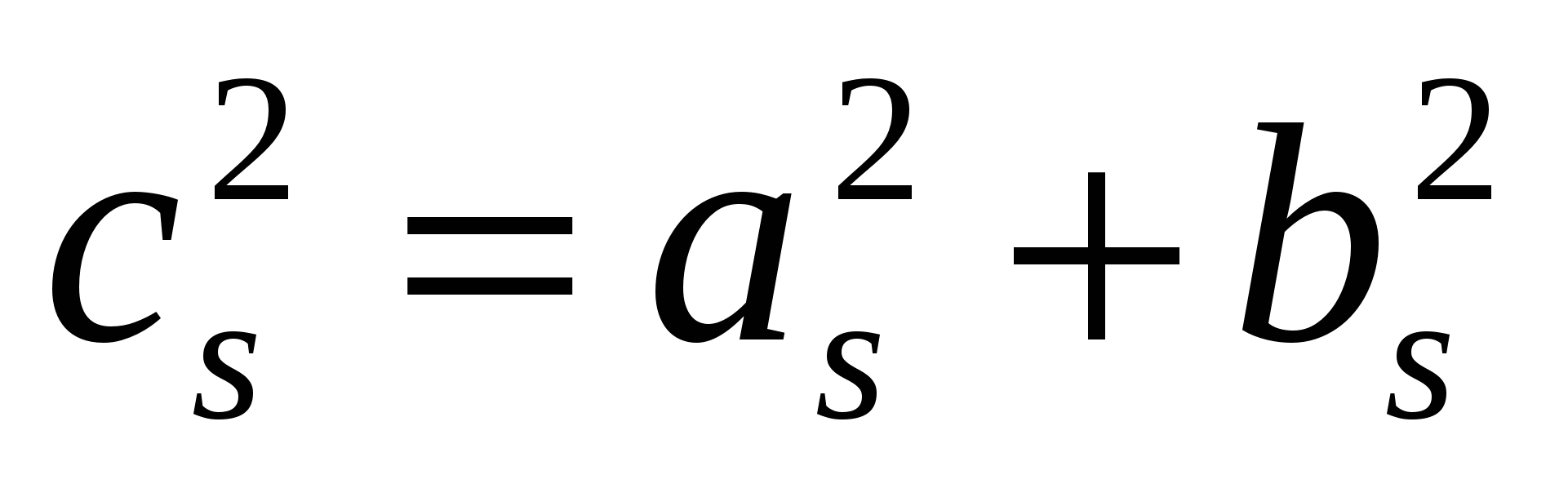 , , 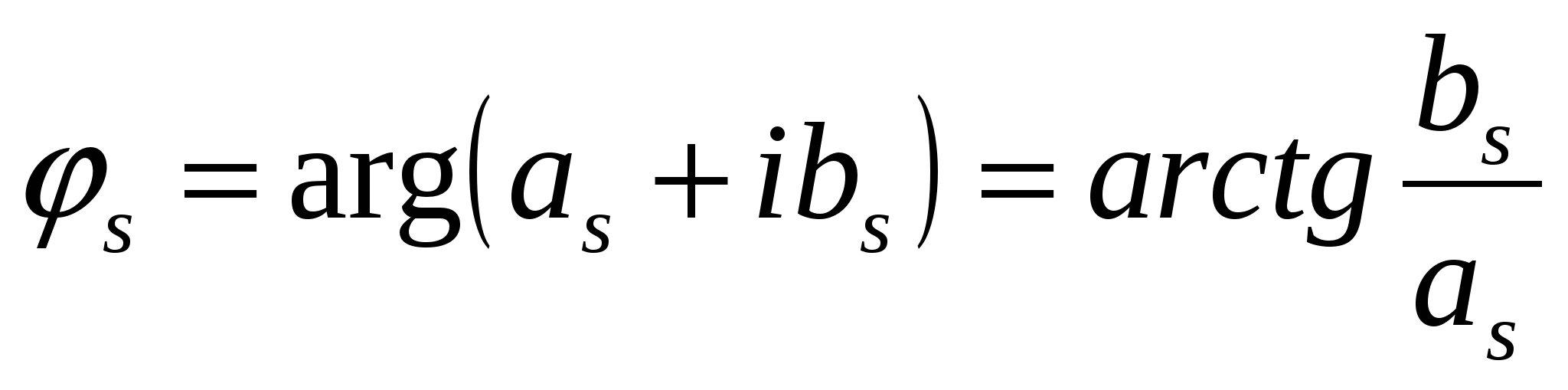
| (2.6) |
Комплексное число 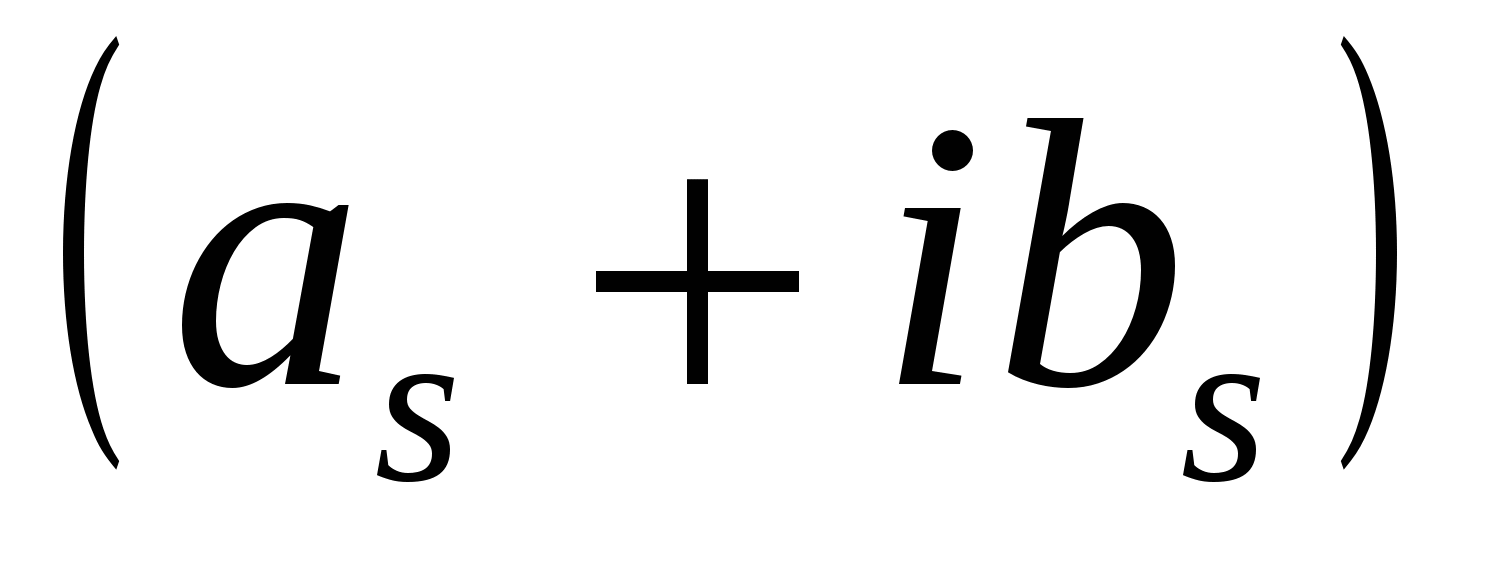 , его модуль
, его модуль 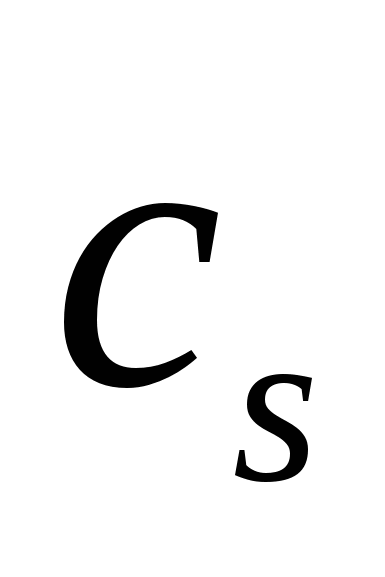 и
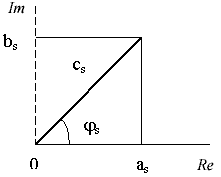
и  аргумент показаны на рис.2.1.
аргумент показаны на рис.2.1.
|
Рис. 2.1. Определение амплитуды 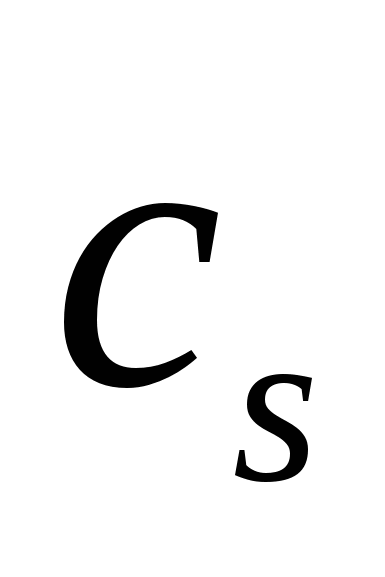 и фазы и фазы  гармоники по коэффициентам гармоники по коэффициентам 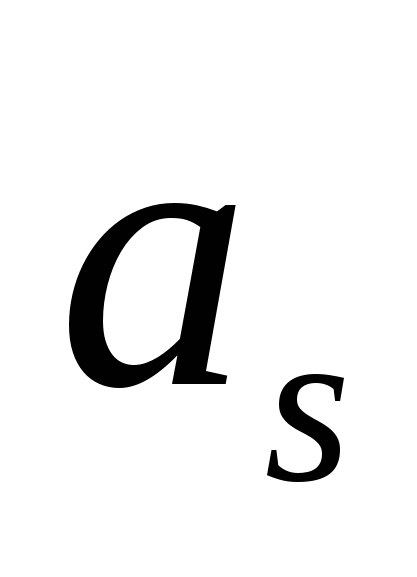 , , 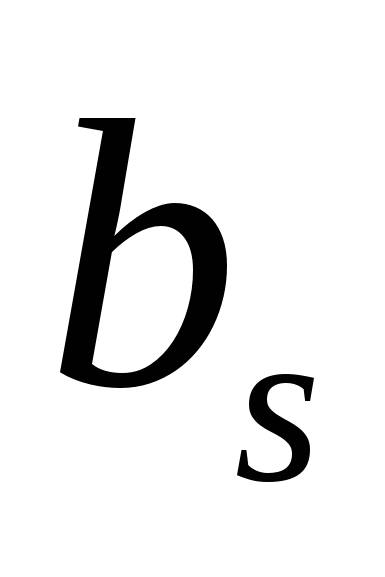 . .
|
Отметим, что величину 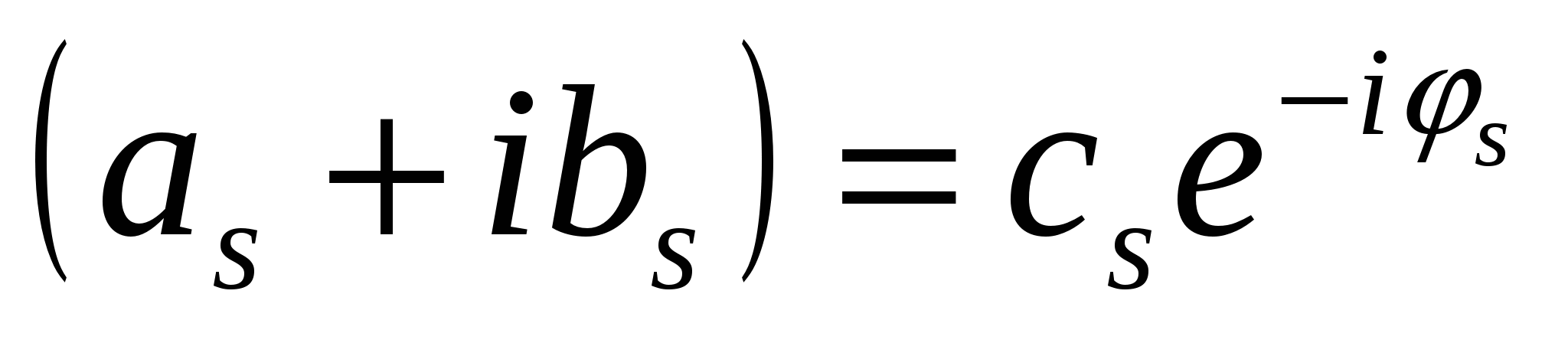 называют комплексной амплитудой гармоники.
называют комплексной амплитудой гармоники.
Для непериодических функций 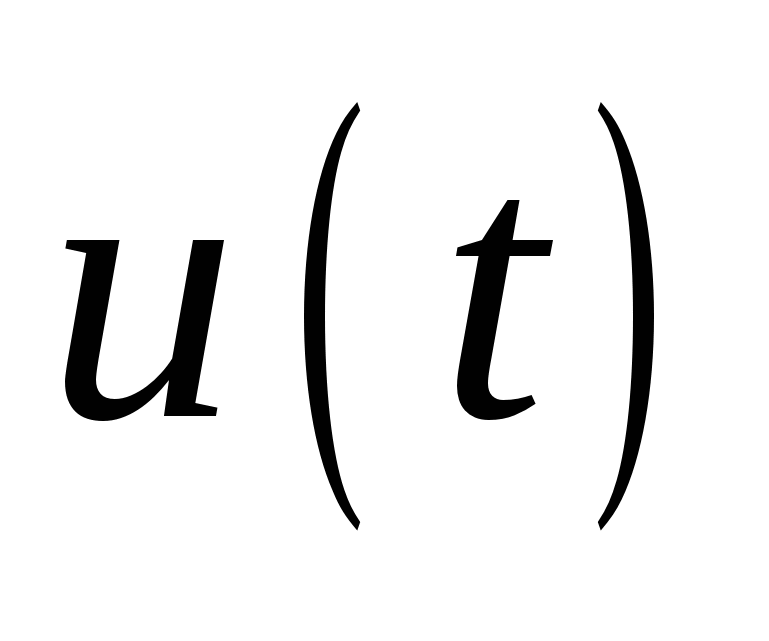 , когда
, когда  , ряд Фурье (11.1) или (11.2) и выражения для его коэффициентов переходят в интегралы Фурье.
, ряд Фурье (11.1) или (11.2) и выражения для его коэффициентов переходят в интегралы Фурье.
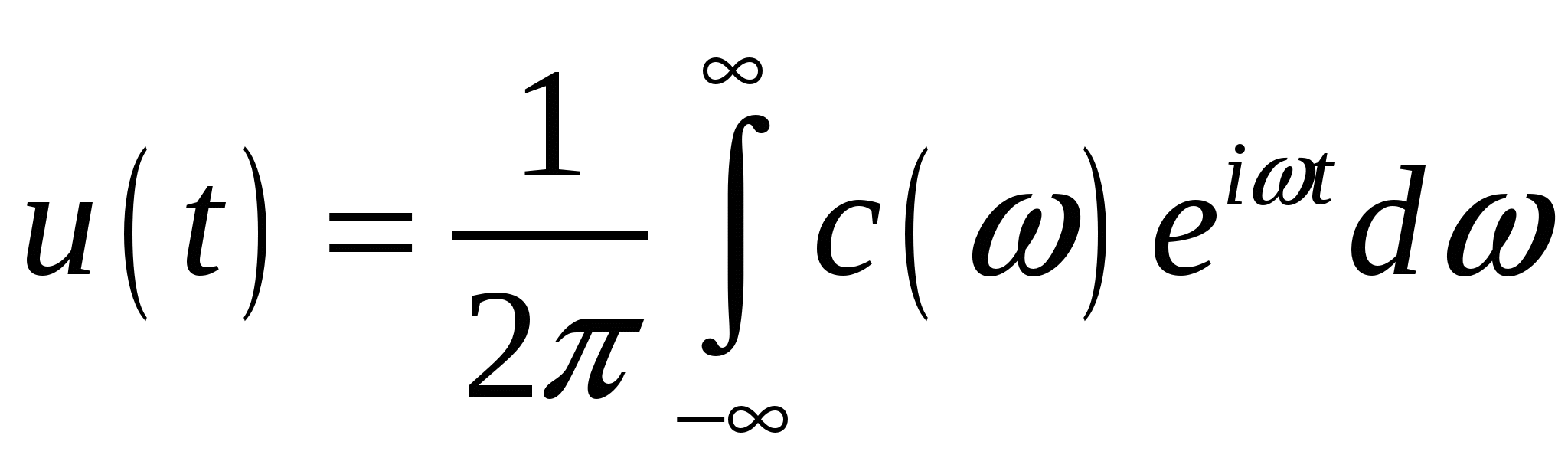
| (2.7) |
- обратное преобразование Фурье,
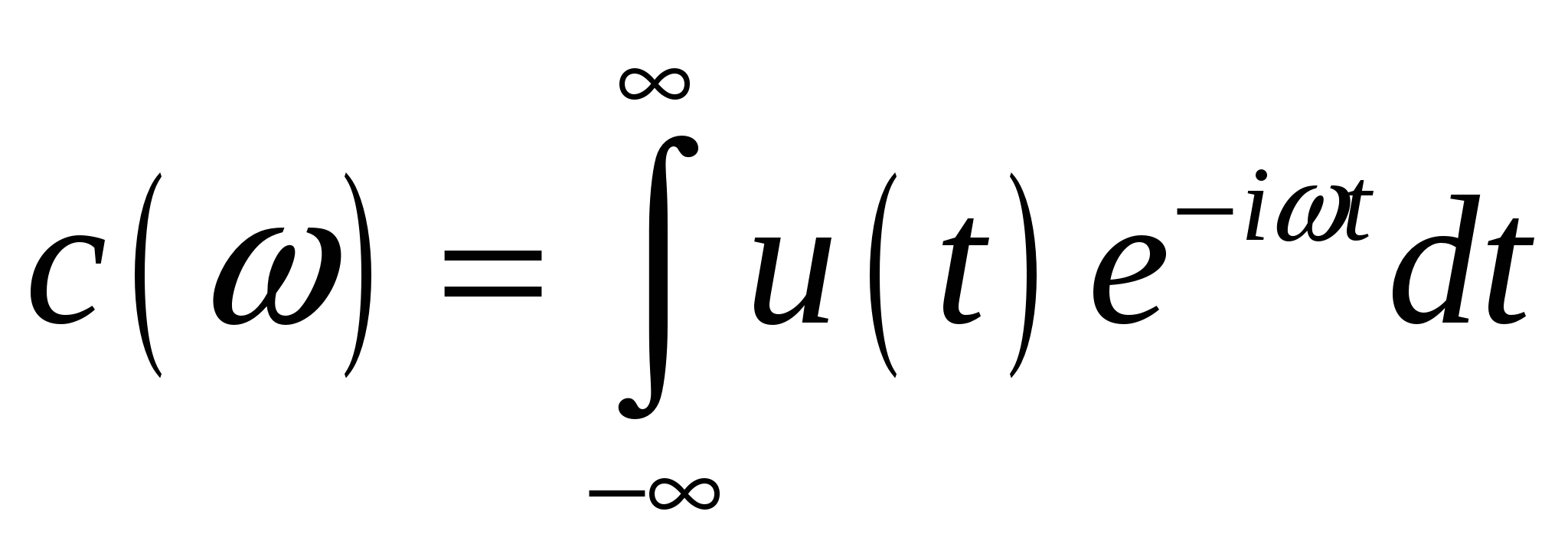
| (2.8) |
- прямое преобразование Фурье.
Дата добавления: 2016-02-20; просмотров: 2888;
