Проверка значимости и интервальная оценка параметров связи

В практических исследованиях о тесноте корреляционной зависимости между рассматриваемыми переменными судят фактически не по величине генерального коэффициента корреляции ρ (который обычно неизвестен), а по величине его выборочного аналога r. Так как r вычисляется по значениям переменных, случайно попавшим в выборку из генеральной совокупности, то в отличие от параметра ρ параметр r — величина случайная.

Пусть вычисленное значение r = 0. Возникает вопрос, объясняется ли это действительно существующей линейной корреляционной связью между переменными X и Y в генеральной совокупности или является следствием случайности отбора переменных в выборку (т.е. при другом отборе возможно, например, r = 0 или изменение знака r).

Обычно в этих случаях проверяется гипотеза H₀: об отсутствии линейной корреляционной связи между переменными в генеральной совокупности, т.е. H₀: ρ = 0. При справедливости этой гипотезы статистика

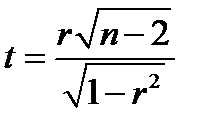(34)

имеет t-распределение Стьюдента с k = n—2 степенями свободы. Поэтому гипотеза H₀ отвергается, т.е. выборочный коэффициент корреляции r значимо (существенно) отличается от нуля, если

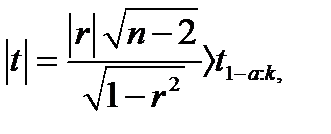(35)

где t_1-a;k — табличное значение t-критерия Стьюдента, определенное на уровне значимости α при числе степеней свободы k = n-2.

Для значимого коэффициента корреляции r целесообразно найти доверительный интервал (интервальную оценку), который с заданной надежностью γ = 1 - α содержит (точнее, «накрывает») неизвестный генеральный коэффициент корреляции ρ. Для построения такого интервала необходимо знать выборочное распределение коэффициента корреляции r, которое при ρ = 0 несимметрично и очень медленно (с ростом п) сходится к нормальному распределению. Поэтому прибегают к специально подобранным функциям от r, которые сходятся к хорошо изученным распределениям. Чаще всего для подбора функции применяют Z-преобразование Фишера.

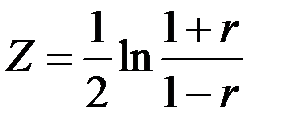. (36)

Распределение уже при небольших п является приближенно нормальным с математическим ожиданием

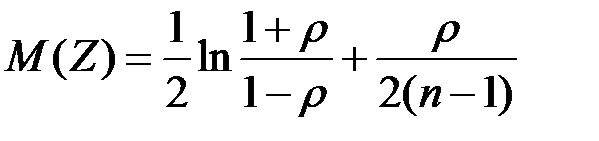(37)

дисперсией 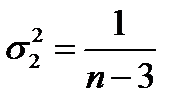(38)

Поэтому вначале строят доверительный интервал для М{z):

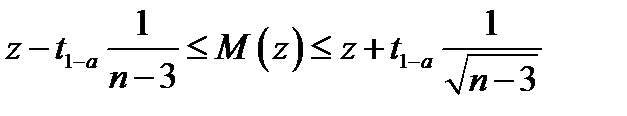(39)

где t_1-α — нормированное отклонение z, определяемое с помощью функции Лапласа:

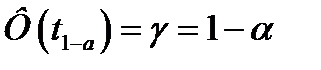(40)

При определении границ доверительного интервала для ρ, т.е. для перехода от z к ρ, существует специальная таблица. При ее отсутствии переход может быть осуществлен по формуле:

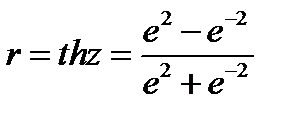(41)

где th z— гиперболический тангенс z.

Если коэффициент корреляции значим, то коэффициенты регрессии b_ух и b_ху также значимо отличаются от нуля, а интервальные оценки для соответствующих генеральных коэффициентов регрессии β_yx и β_xy могут быть получены по формулам, основанным на том, что статистики (b_yx-β_xy)/S_byx , (b_xy-β_yx)\S_bxy имеют t-распределение Стьюдента с (n—2) степенями свободы:

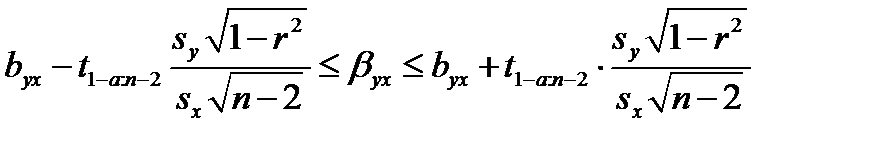(42)

(43)