ОСНОВНЫЕ ПОЛОЖЕНИЯ КОРРЕЛЯЦИОННОГО АНАЛИЗА

Понятия корреляции и регрессии появились в середине XIX в. благодаря работам английских статистиков Ф. Гальтона и К. Пирсона. Первый термин произошел от латинского «correlatio» — соотношение, взаимосвязь. Второй термин (от лат. «regressio» — движение назад) введен Ф. Гальтоном, который, изучая зависимость между ростом родителей и их детей, обнаружил явление «регрессии к среднему» — у детей, родившихся у очень высоких родителей, рост имел тенденцию быть ближе к средней величине.

В естественных науках часто речь идет о функциональной зависимости (связи), когда каждому значению одной переменной соответствует вполне определенное значение другой (например, скорость свободного падения тела в вакууме в зависимости от времени и т.п.).

В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость получила название статистической (или стохастической, вероятностной).

Возникновение понятия статистической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками. Примером статистической связи является зависимость урожайности от количества внесенных удобрений, производительности труда на предприятии от его энерговооруженности и т.п.

В силу неоднозначности статистической зависимости между Y и X для исследователя, в частности, представляет интерес усредненная по x схема зависимости, т.е. закономерность в изменении условного математического ожидания М_Х(Y) (математического ожидания случайной переменной Y, вычисленного в предположении, что переменная X приняла значение х в зависимости от х.

Определение. Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

Корреляционная зависимость может быть представлена в виде:

М_х(Y)=φ(x) (1) или М_Y(X)=φ(y) (2)

Уравнения (1) и (2) называются модельными уравнениями регрессии (или просто уравнениями регрессии) соответственно Y по X и X по Y, функции φ(х) и ψ(у) - модельными функциями регрессии (или функциями регрессии), а их графики — модельными линиями регрессии (или линиями регрессии).

Для отыскания модельных уравнений регрессии, вообще говоря, необходимо знать закон распределения двумерной случайной величины (Х,Y). На практике исследователь, как правило, располагает лишь выборкой пар значений (х_i, у_i) ограниченного объема. В этом случае речь может идти об оценке (приближенном выражении) по выборке функции регрессии. Такой наилучшей (в смысле метода наименьших квадратов) оценкой является выборочная линия (кривая) регрессии Y по X:

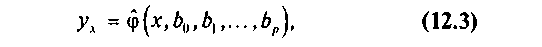(3)

где y_х — условная (групповая) средняя переменной Y при фиксированном значении переменной Х= х; b₀,b₁…b_p — параметры кривой.

Аналогично определяется выборочная линия (кривая) регрессии Х по Y:

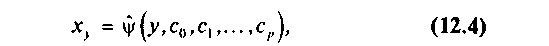(4)

где х_у — условная (групповая) средняя переменной X при фиксированном значении переменной Y = у; c₀,c₁,...,c_p — параметры кривой.

Уравнения (3), (4) называют также выборочными уравнениями регрессии соответственно Y по X и X по Y.

Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа.

Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа — выявление связи между случайными переменными и оценка ее тесноты.