Коэффициент корреляции. Перейдем к оценке тесноты корреляционной зависимости

Перейдем к оценке тесноты корреляционной зависимости. Рассмотрим наиболее важный для практики и теории случай линейной зависимости вида (16).

На первый взгляд подходящим измерителем тесноты связи Y от X является коэффициент регрессии Ь_уx ибо, как уже отмечено, он показывает, на сколько единиц в среднем изменяется Y, когда X увеличивается на одну единицу. Однако Ь_уx зависит от единиц измерения переменных. Например, в полученной ранее зависимости он увеличится в 1000 раз, если величину основных производственных фондов X выразить не в млн руб., а в тыс. руб. Очевидно, что для «исправления» Ь_уx как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Статистика знает такую систему единиц. Эта система использует в качестве единицы измерения переменной ее среднее квадратическое отклонение S.

Представим уравнение (16) в эквивалентном виде:

(28)

В этой системе величина

(29)

показывает, на сколько величин S_y изменится в среднем Y, когда X увеличится на одно S_x Величина r является показателем тесноты связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).

На рис. 2 приведены две корреляционные зависимости переменной Y по X. Очевидно, что в случае а) зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б), так как точки корреляционного поля а) дальше отстоят от линии регрессии, чем точки поля б). Нетрудно видеть, что r совпадает по знаку с Ь_уx (а значит, и с Ь_ху).

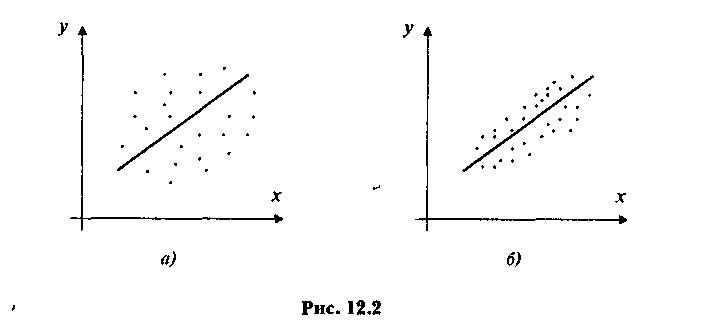
Рис. 2

Если r > 0 (Ь_ух>0, Ь_ху>0), то корреляционная связь между переменными называется прямой, если r< О (Ь_уx <0, Ь_ху<0) — обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.

Учитывая (17), формулу для r представим в виде:

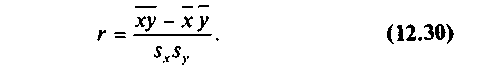
Отсюда видно, что формула для r симметрична относительно двух переменных, т.е. переменные Х и Y можно менять местами. Тогда аналогично (24) можно записать:

Найдя произведение обеих частей равенств (29) и (31), получим

т.е. коэффициент корреляции r переменных X и Y есть средняя геометрическая коэффициентов регрессии, имеющая их знак.