Дискретное преобразование Фурье (ДПФ).

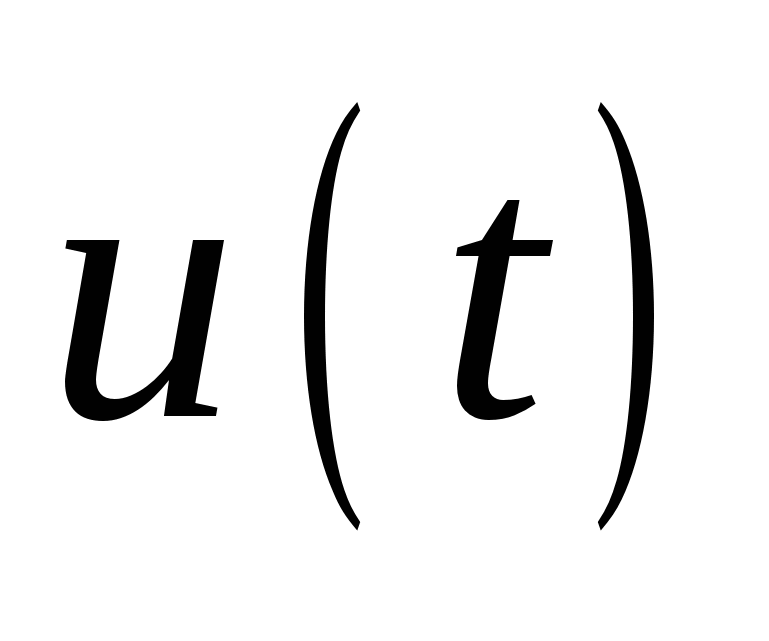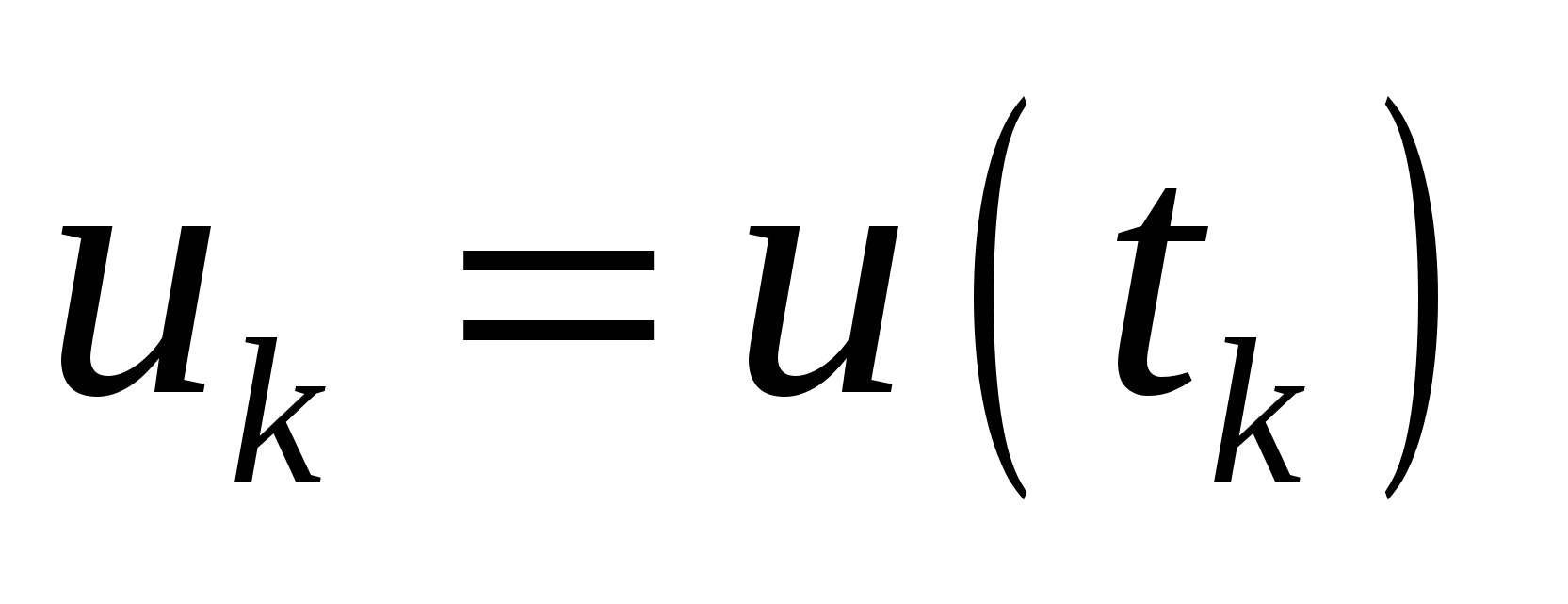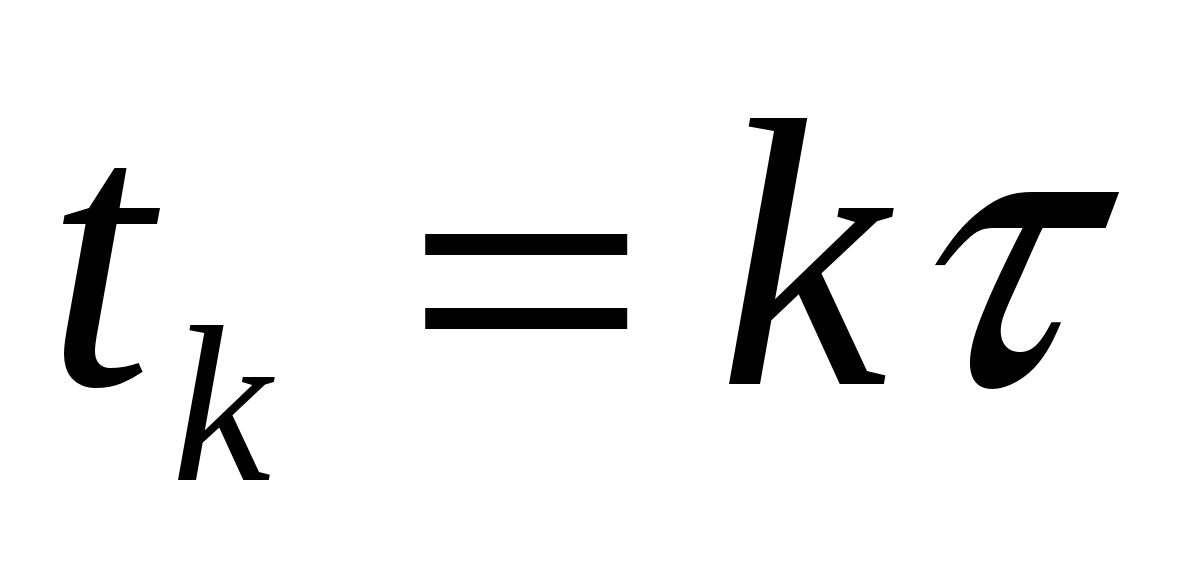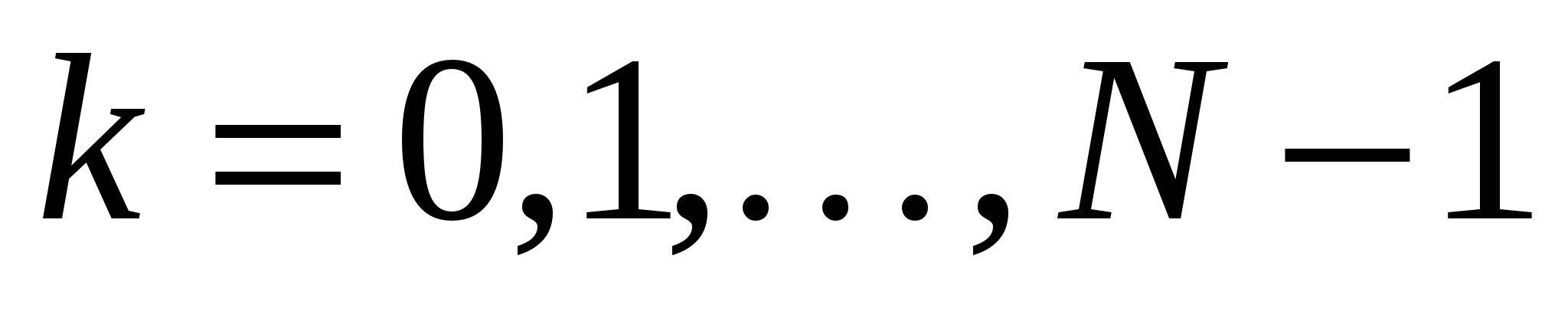ДПФ позволяет вычислять спектр дискретного сигнала, в том числе полученного из аналогового сигнала выборкой его значений , , . Оно основано на следующих положениях.
1. Сигнал является периодическим или периодически продолженным, 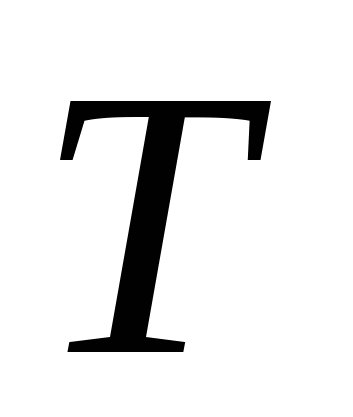- период.
2. Сигнал является дискретным и имеет постоянный шаг дискретизации .
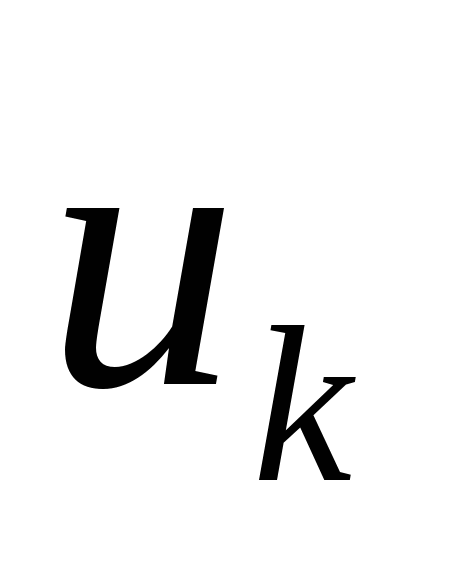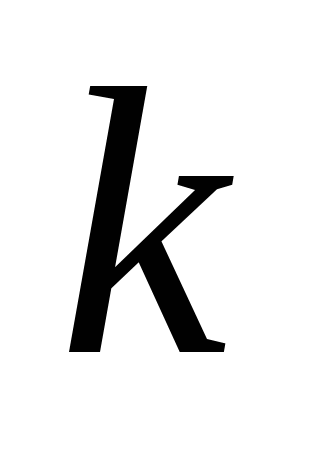3. Отсчеты сигнала на периоде представляются массивом , где – номера отсчетов, .
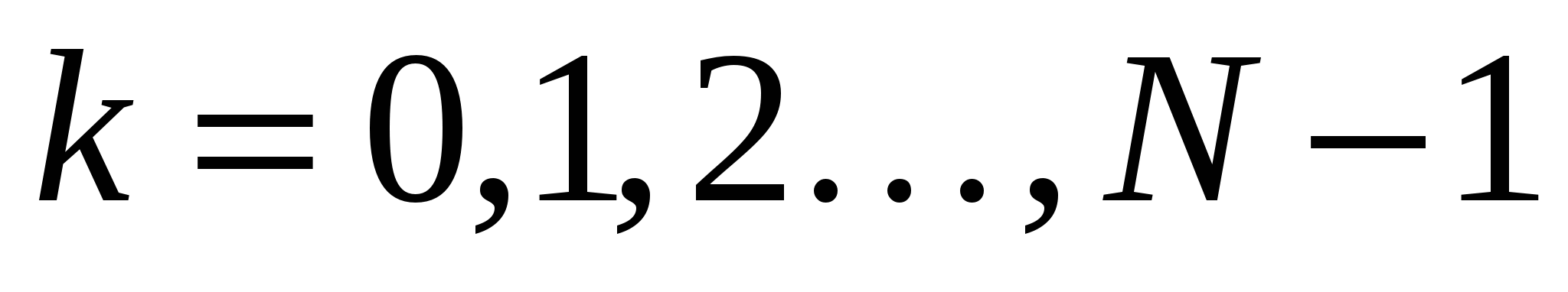4. Количество отсчетов на периоде равно .
5. Условие периодичности сигнала имеет вид 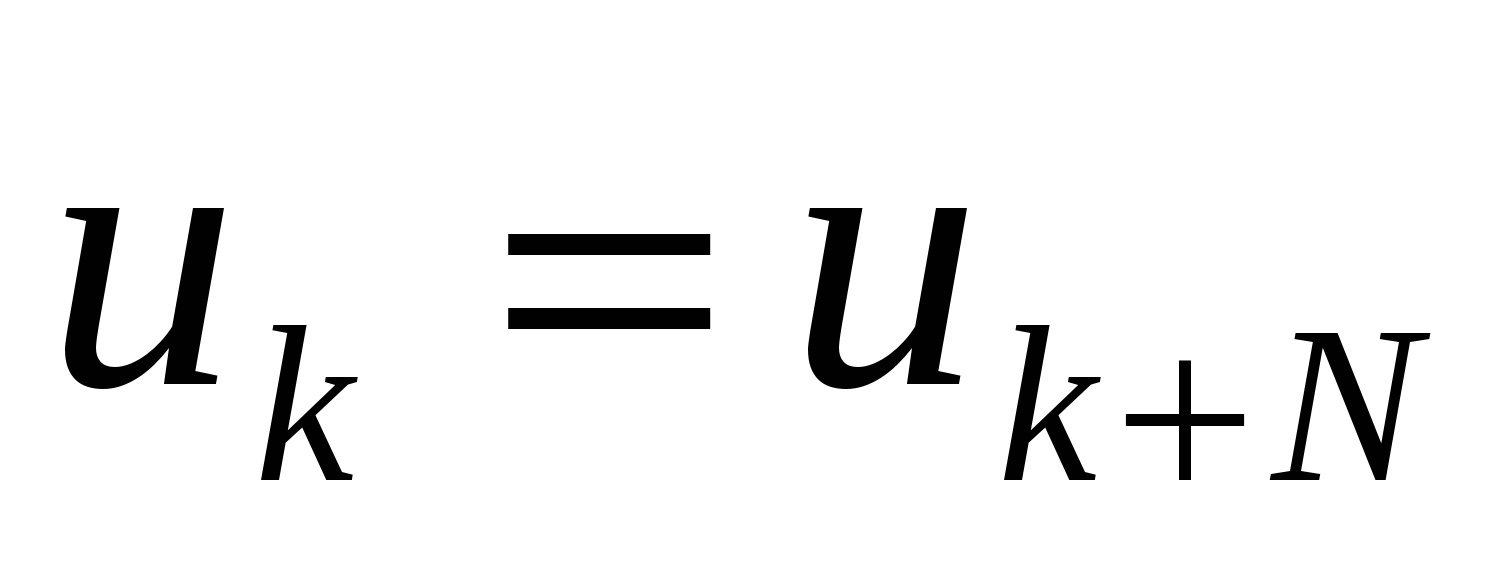, т.е. .
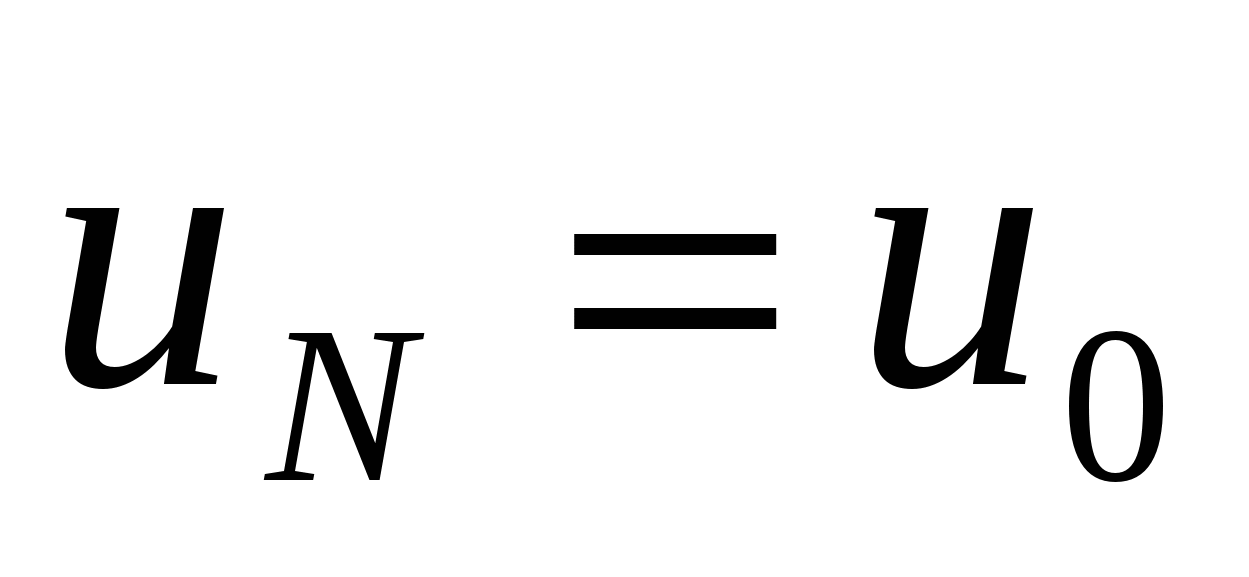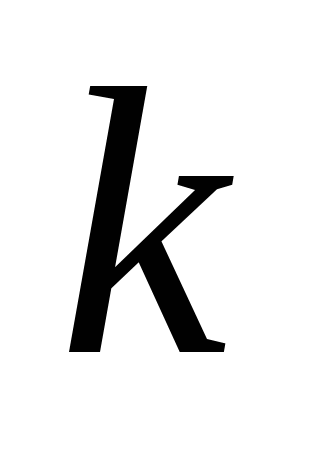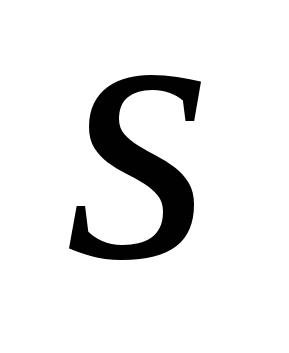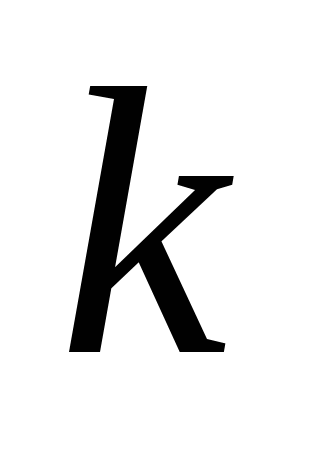6. Формулы ДПФ записываются в безразмерных целых переменных , , где – номера отсчетов сигнала, 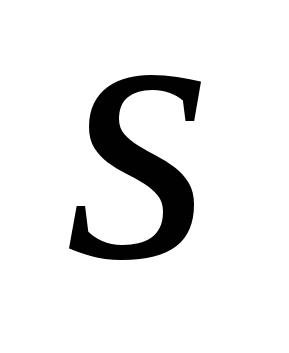– номера спектральных составляющих.
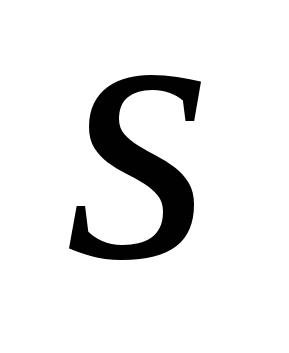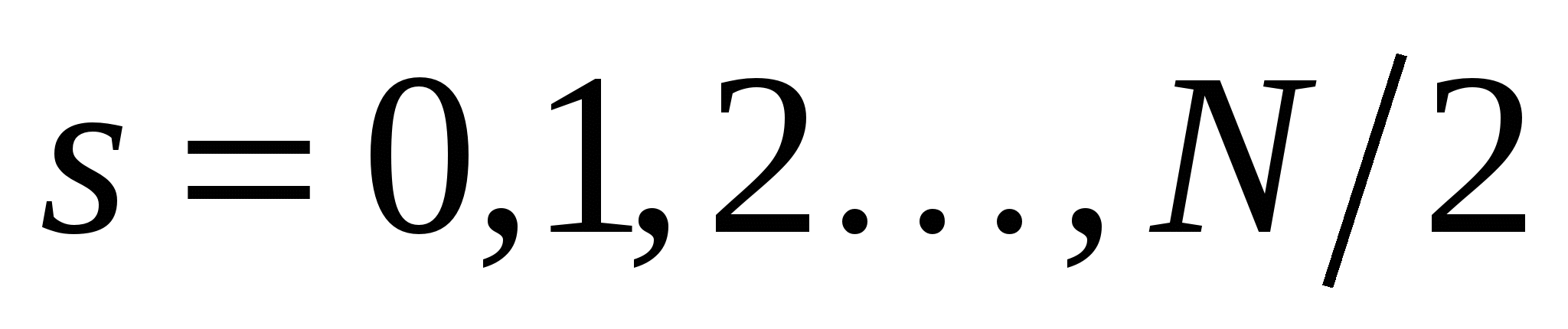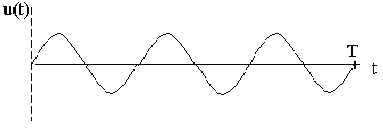
7. Номера – это номера гармоник. Для вещественного сигнала (комплексный будет рассмотрен позже) значения для четного , т.е. гармоник вдвое меньше, чем отсчетов сигнала. Нечетные значения возможны, но мы их рассматривать не будем. Значение 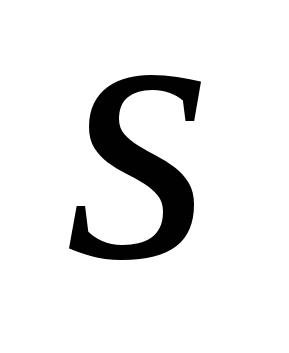показывает количество полных колебаний на периоде. Например, на рис.11.2 показан гармонический сигнал для .
8. Для каждой гармоники определяются ее амплитуда и фаза. В вычислениях амплитуд и фаз используются 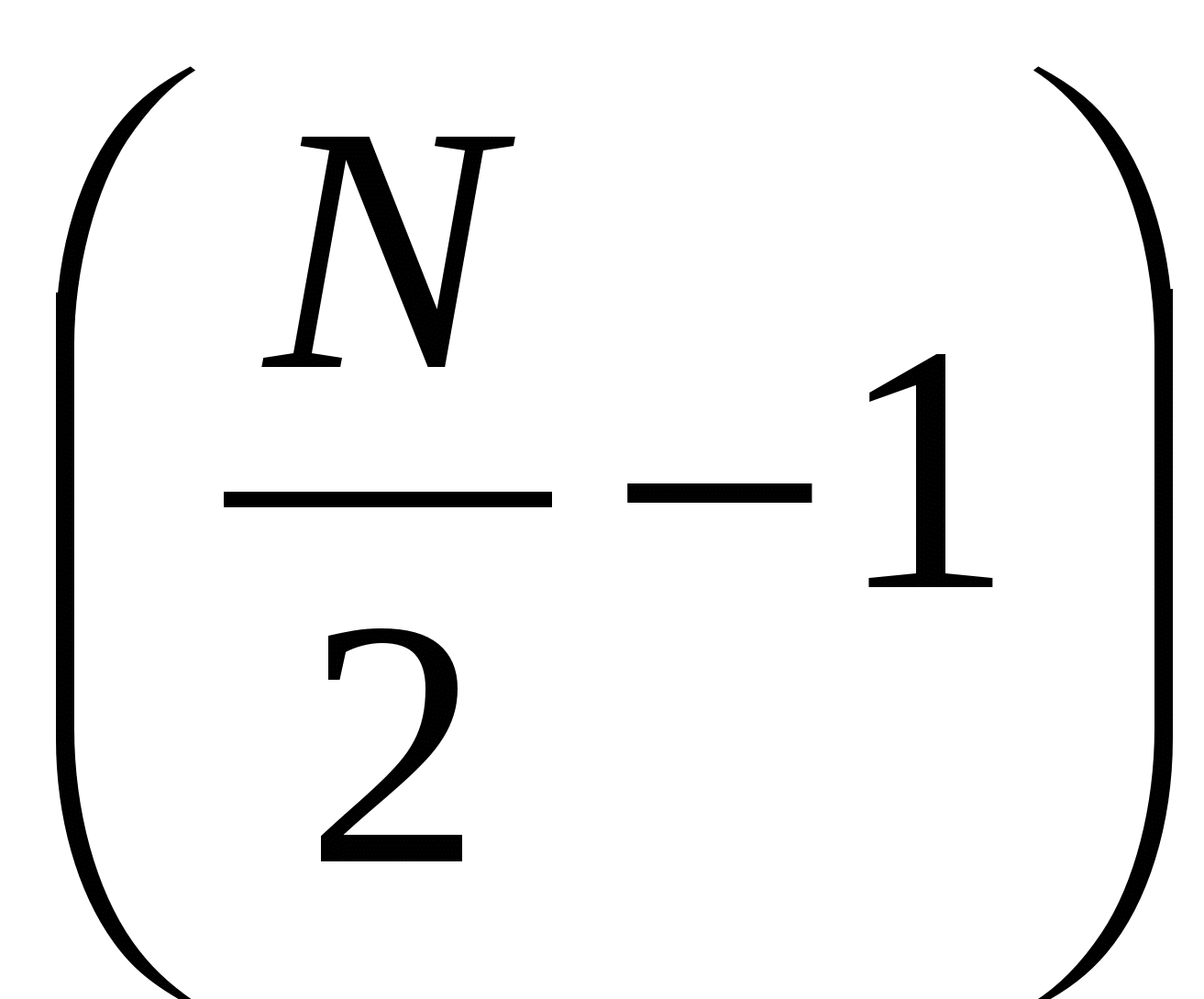синусных составляющих и 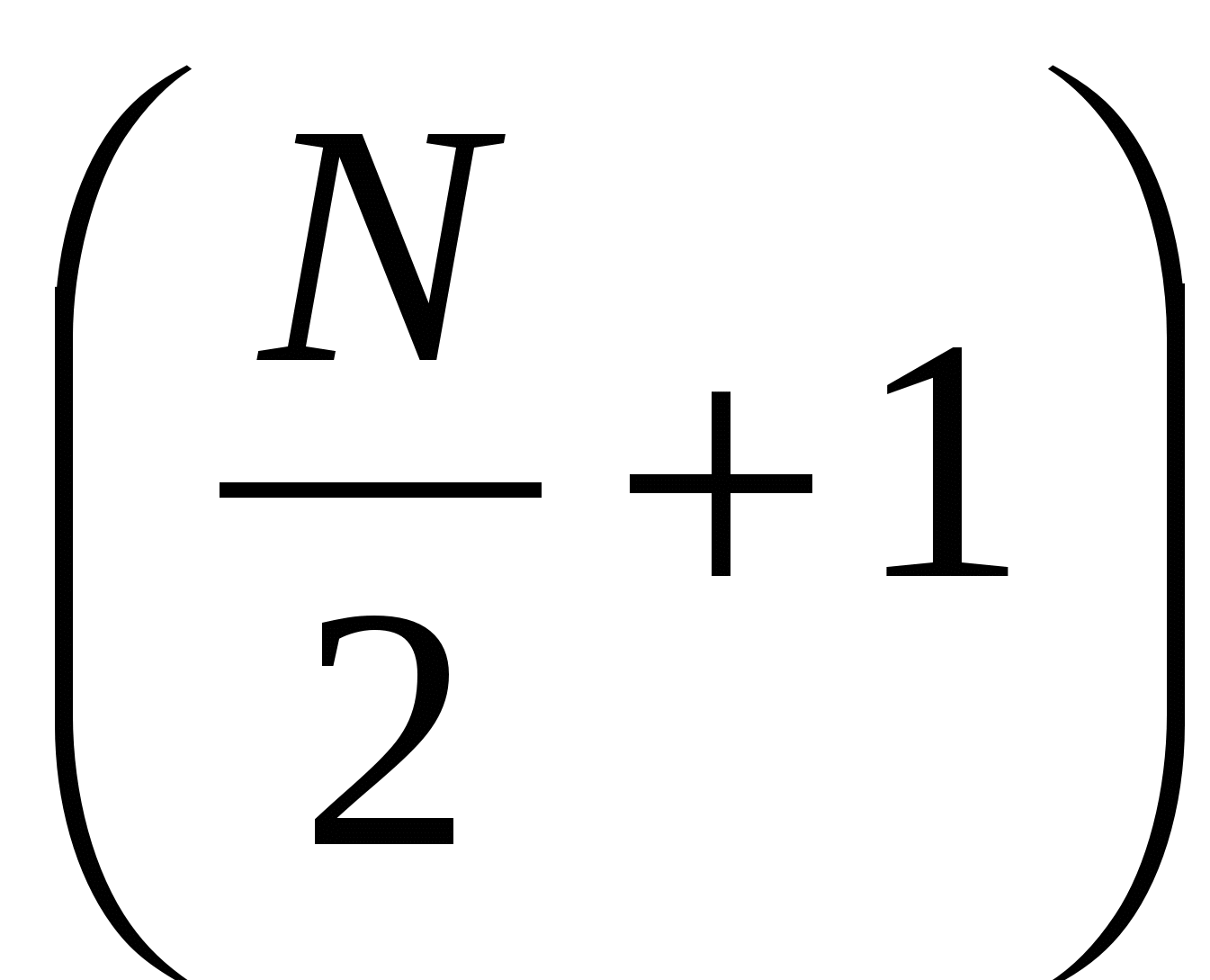косинусных составляющих, т.к. две синусные составляющие и 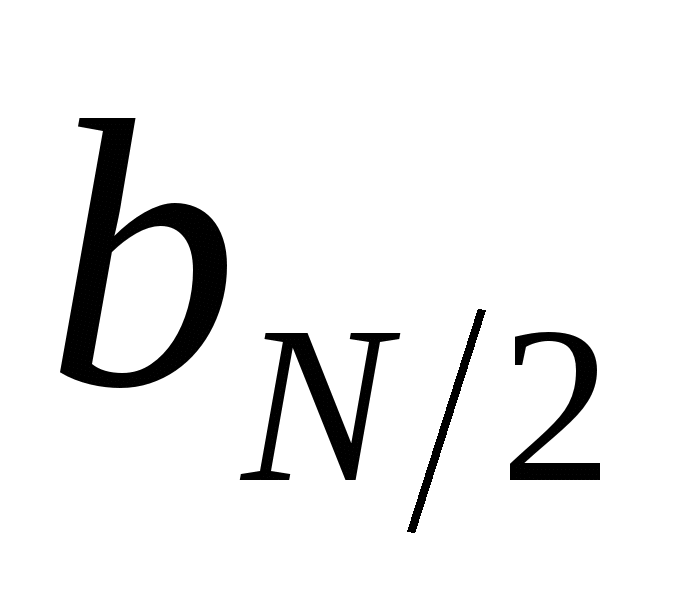являются нулевыми и не учитываются в формулах.

Рис. 2.2. Гармонический сигнал для