Алгоритм Преобразование НКА в ДКА

Вход: НКА .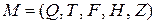

Выход: ДКА .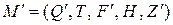

Шаг 1. Пометить первый столбец таблицы переходов 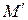ДКА начальным состоянием (множеством начальных состояний) НКА .

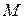Шаг 2. Заполняем очередной столбец таблицы переходов 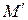, помеченный символами 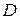, для этого определяем те состояния 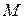, которые могут быть достигнуты из каждого символа строки 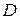при каждом входном символе 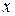. Поместить каждое найденное множество 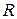(в том числе 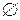) в соответствующие позиции столбца 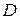таблицы 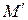, т.е.:

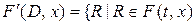для некоторого }

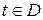Шаг 3. Для каждого нового множества 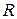(кроме 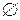), полученного в столбце 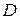таблицы переходов 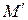, добавить новый столбец в таблицу, помеченный .

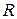Шаг 4. Если в таблице переходов КА 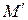есть столбец с незаполненными позициями, то перейти к шагу 2.

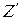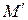Шаг 5. Во множество ДКА включить каждое множество, помечающее столбец таблицы переходов 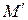и содержащее 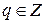НКА .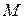

Шаг 6. Составить таблицу новых обозначений множеств состояний и определить ДКА 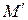в этих обозначениях.

Этот алгоритм обеспечивает отсутствие недостижимых состояний ДКА, но не гарантирует его минимальности.

Пример Пример 2.1.Дана регулярная грамматика 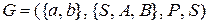с правилами 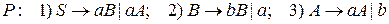. Построить по регулярной грамматике КА и преобразовать полученный автомат к детерминированному виду.

Построим по НКА 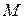из примера 2.1 ДКА .

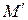1 Строим таблицу переходов для ДКА 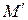(таблица 2.2).

Таблица 2.2 – Построение функции переходов для ДКА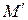

Шаг
F	S	A, B	A, N	B, N	A	N	B
a	A, B	A, N	A	N	A		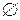N
b		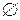B, N	N	B	N		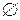B

2 Во множество заключительных состояний автомата 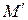включим элементы .

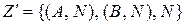3 Введем следующие новые обозначения состояний автомата 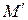: (A,B)=С, (A, N)=D, (B, N)=E.

4 Искомый ДКА определяется следующей пятеркой объектов: 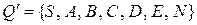, , 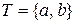функция переходов задана таблицей 2.3, , .

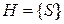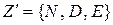Таблица 2.3 – Функция переходов для ДКА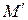

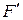
	S	A	B	С	D	E	N
a	C	A	N	D	A	N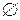
b		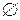N	B	E	N	B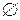

Граф полученного ДКА представлен на рисунке 2.1.

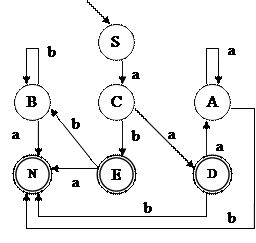Рисунок 2.1 – Граф ДКА