Алгоритм Объединение эквивалентных состояний КА
Вход: КА 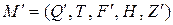 без недостижимых состояний.
без недостижимых состояний.
Выход: минимальный КА 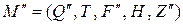 .
.
Шаг 1. На первом шаге строим нулевое разбиение R(0), состоящее из двух классов эквивалентности: заключительные состояния КА - Z и не заключительные - Q-Z.
Шаг 2. На очередном шаге построения разбиения R(n) в классы эквивалентности включить те состояния, которые по одинаковым входным символам переходят в n-1 эквивалентные состояния, т.е.
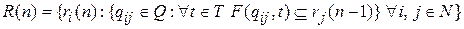 .
.
Шаг 3. До тех пор, пока R(n) ¹ R(n-1) полагаем n=n+1 и идем к шагу 2.
Шаг 4. Переобозначить оставшиеся неразбитые группы состояний и включить их в таблицу новых обозначений состояний автомата.
Шаг 5. Определить эквивалентный КА 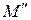 в новых обозначениях.
в новых обозначениях.
ПримерМинимизировать конечный автомат из предыдущего примера.
Последовательность построения разбиений будет иметь вид:
R(0) = {{A, B, C}, {D, E}}, n = 0;
R(1) = {{A}, {B, C}, {D, E}}, n = 1;
R(2) = {{A}, {B, C}, {D, E}}, n=2.
Т.к. R(1) = R(2), то искомое разбиение построено.
Переобозначим оставшиеся неразбитые группы состояний:
X={B, C}, Y={D, E}.
Получим минимальный автомат 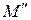 , где
, где 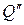 ={A, X, Y},
={A, X, Y}, 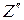 ={Y}.
={Y}.
Функция переходов автомата 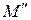 представлена в таблице 2.7.
представлена в таблице 2.7.
Таблица 2.6 - Функция переходов автомата 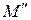
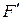
| A | X | Y |
| a | X | X | |
| b | X | Y | Y |
Граф переходов конечного автомата после его минимизации показан на рисунке 2.4.
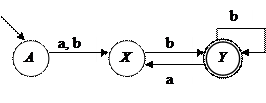 |
Рисунок 2.4 – Граф минимального ДКА 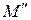
Дата добавления: 2016-03-27; просмотров: 1366;
