Формулы ДПФ для вещественного сигнала.

Пусть рассматривается сигнал 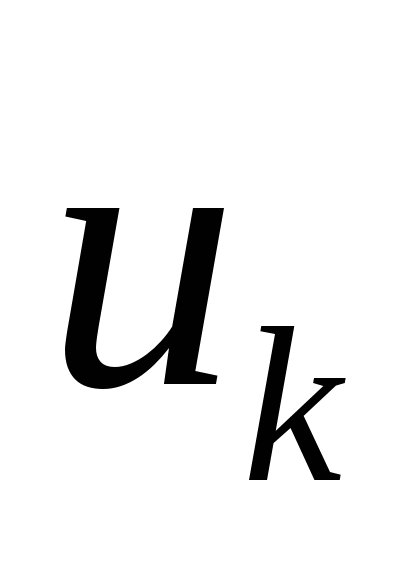, 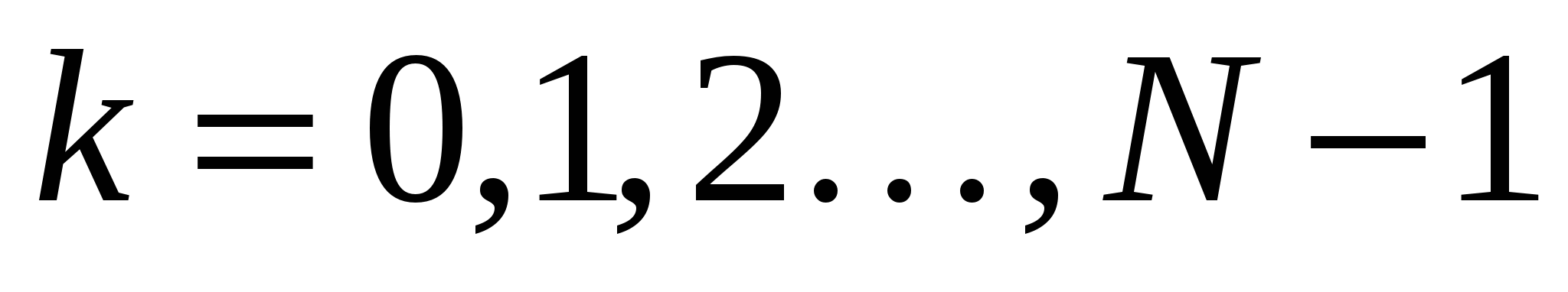. По отсчетам 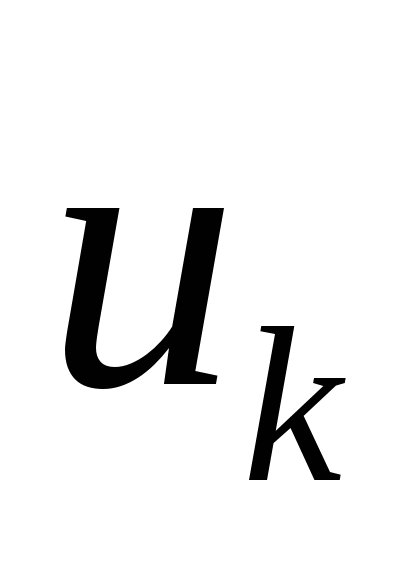можно найти значений коэффициентов 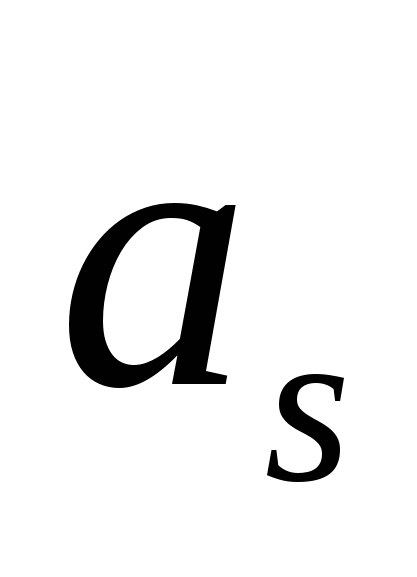, , 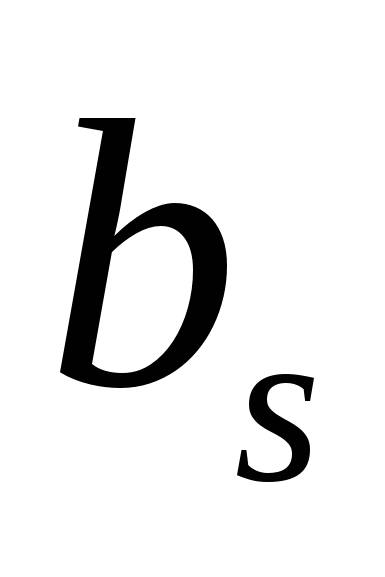в том числе 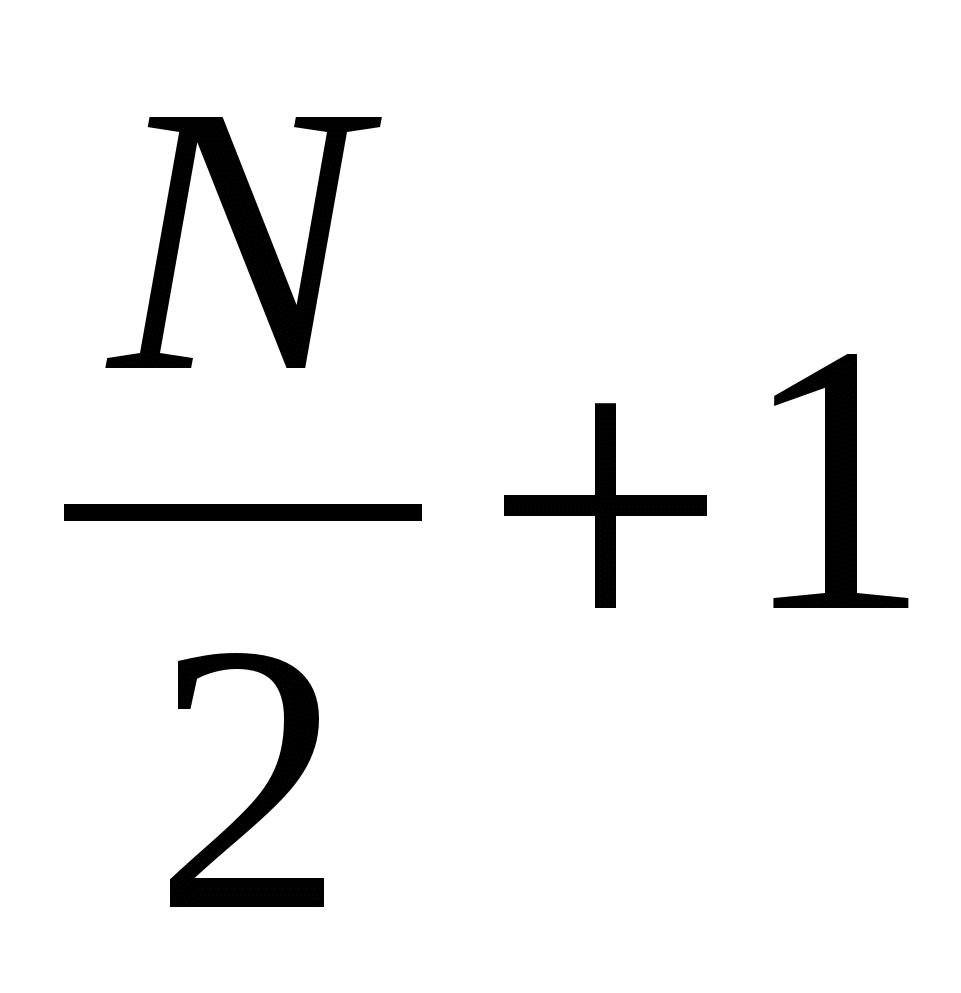значени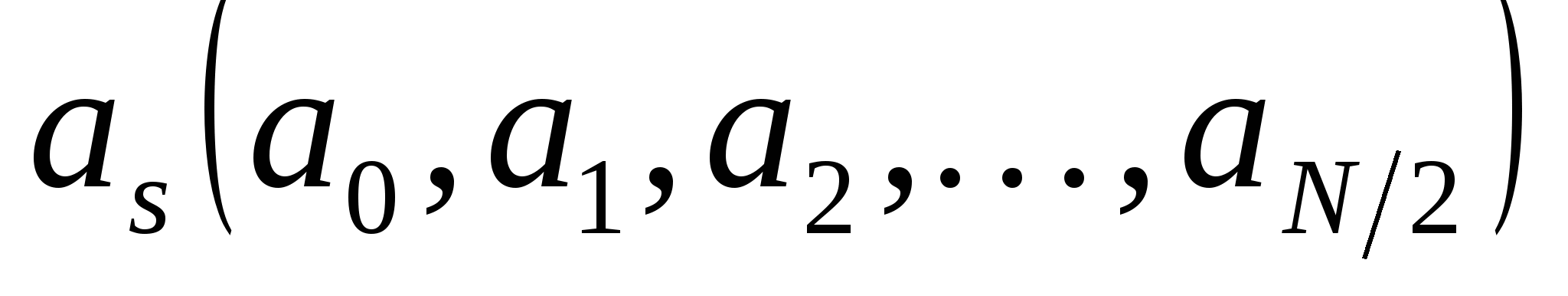й и 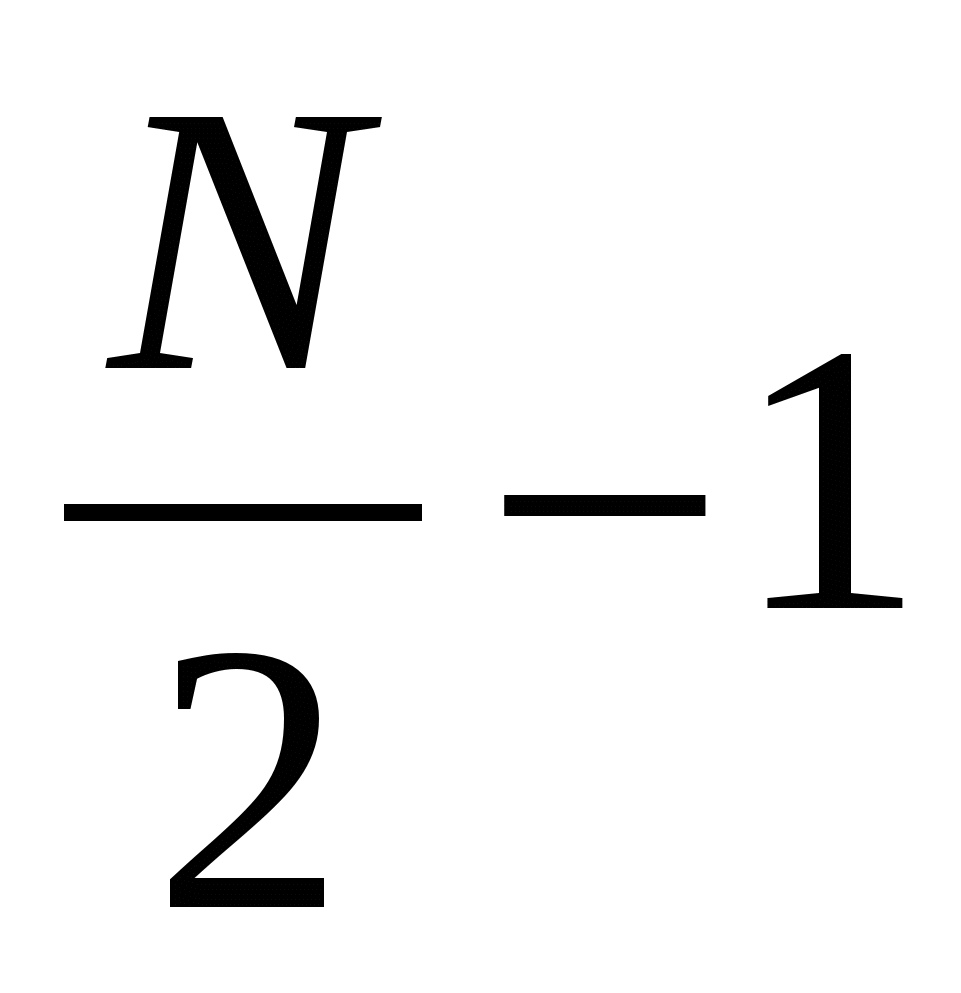значений 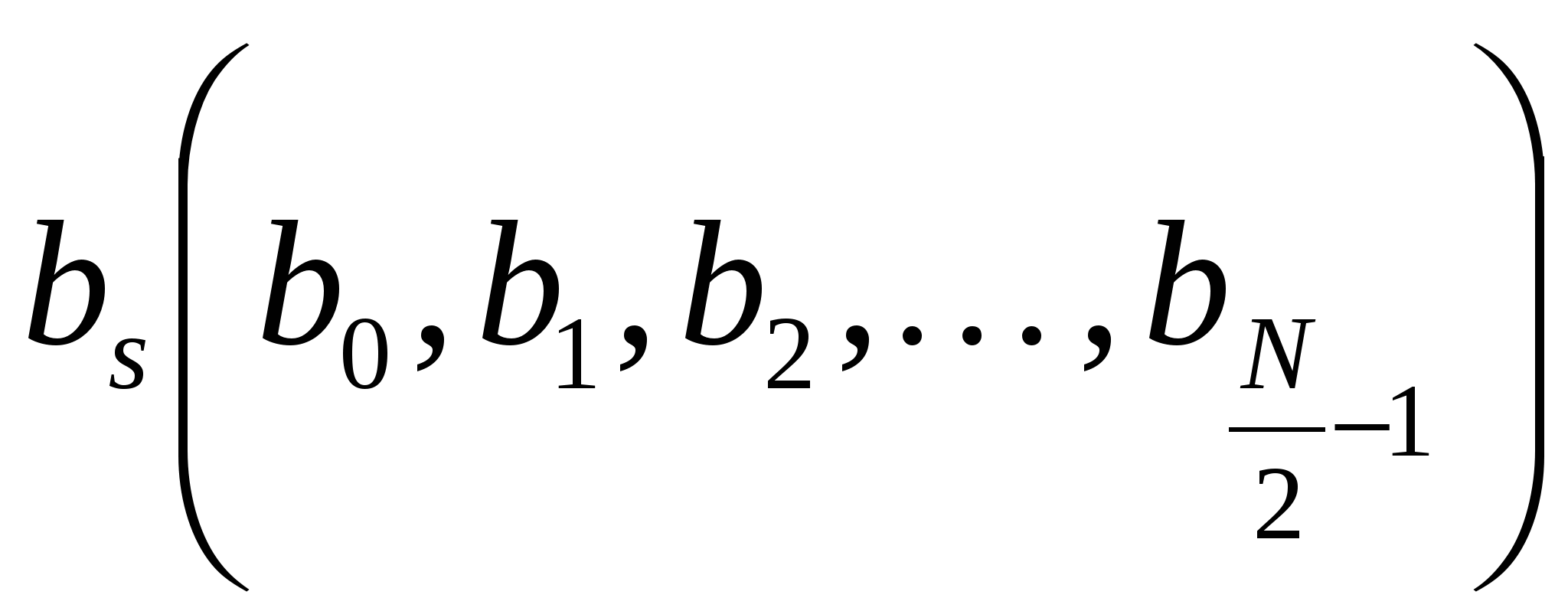. Эти коэффициенты определяют среднее значение сигнала 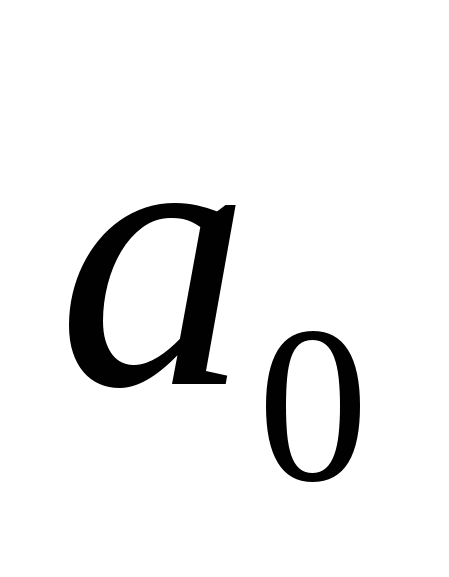и 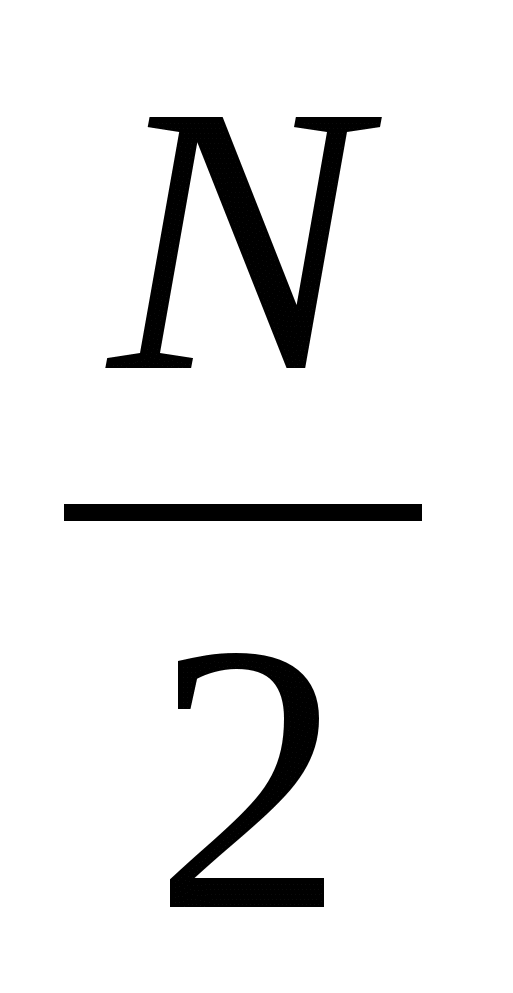гармоник сигнала, 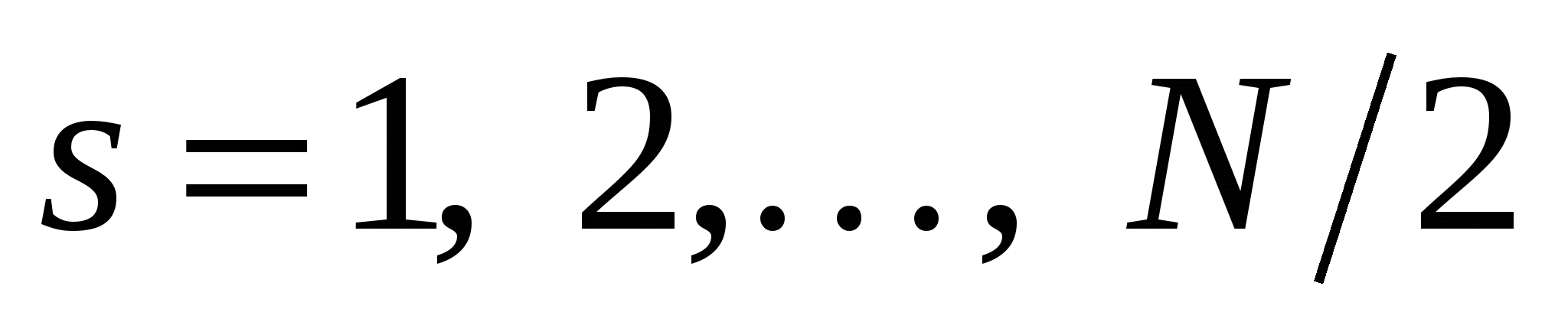. Поэтому в ДПФ получается только отрезок ряда Фурье, который в размерных переменных имеет вид

, , .

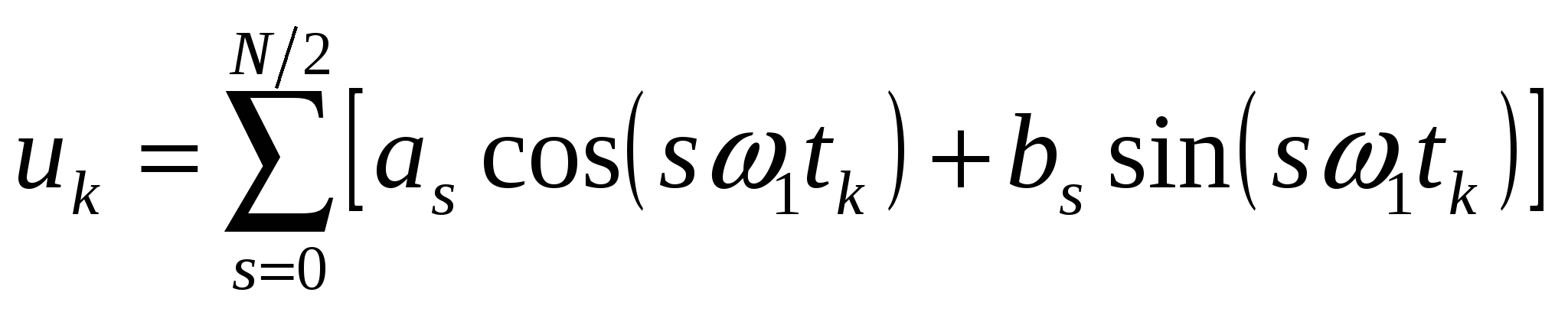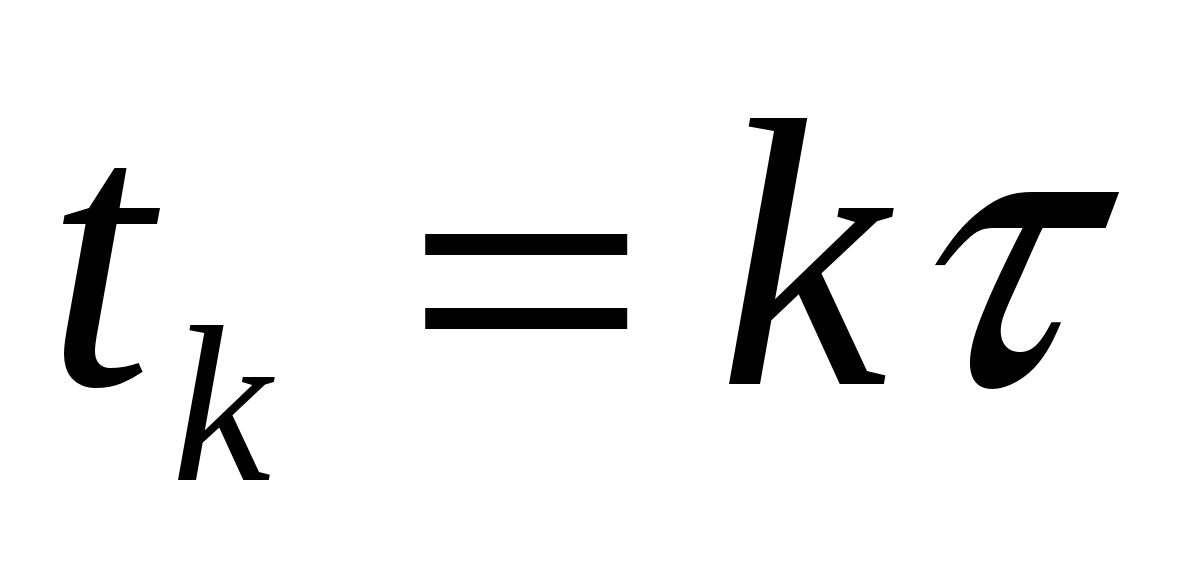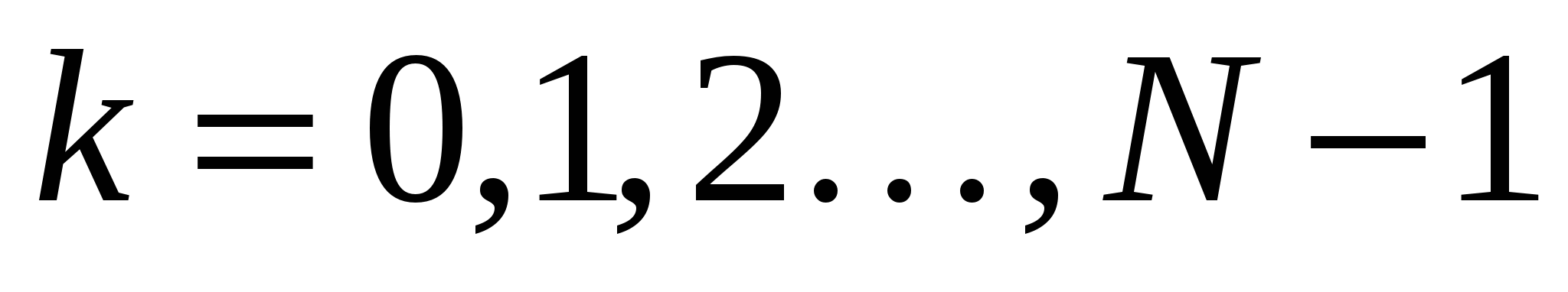(2.10)

или

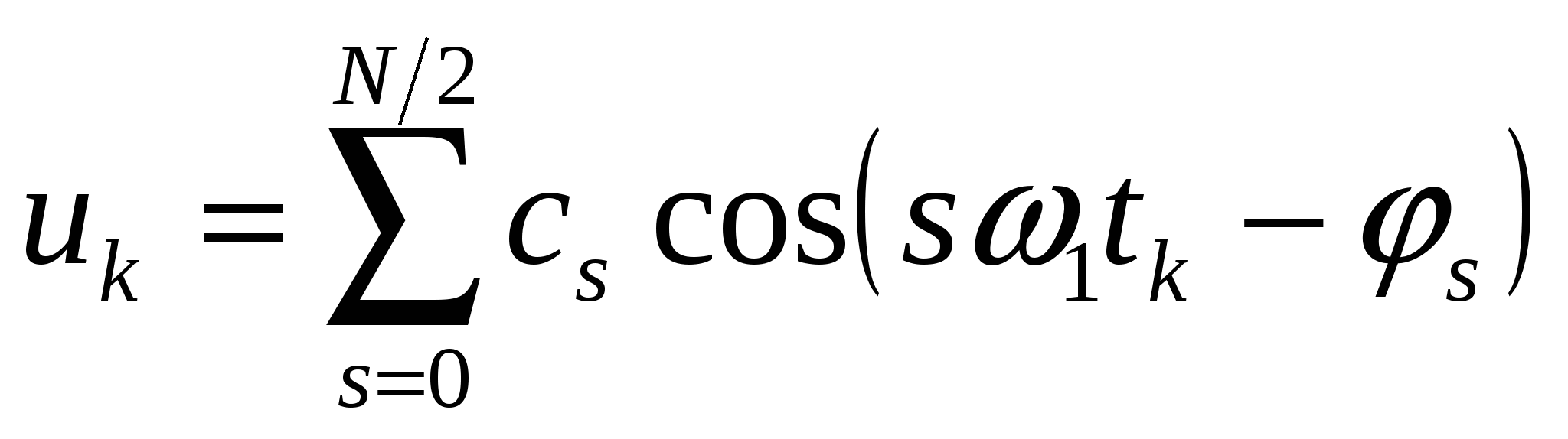
(2.11)

Это обратное ДПФ. Прямое ДПФ определено формулами для коэффициентов 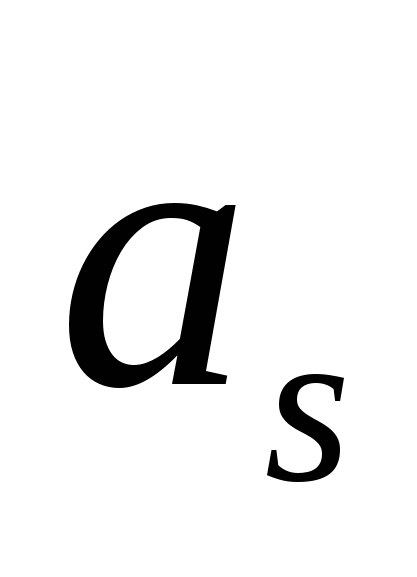, 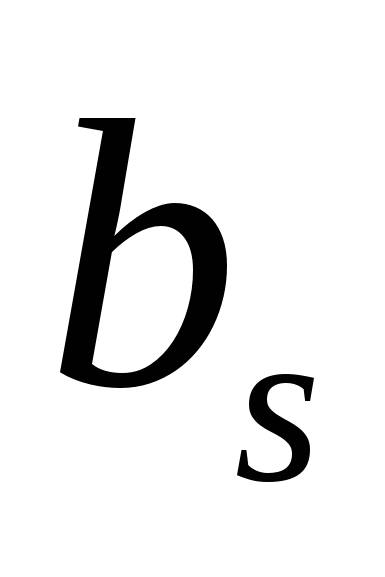при переходе от интегралов к суммам

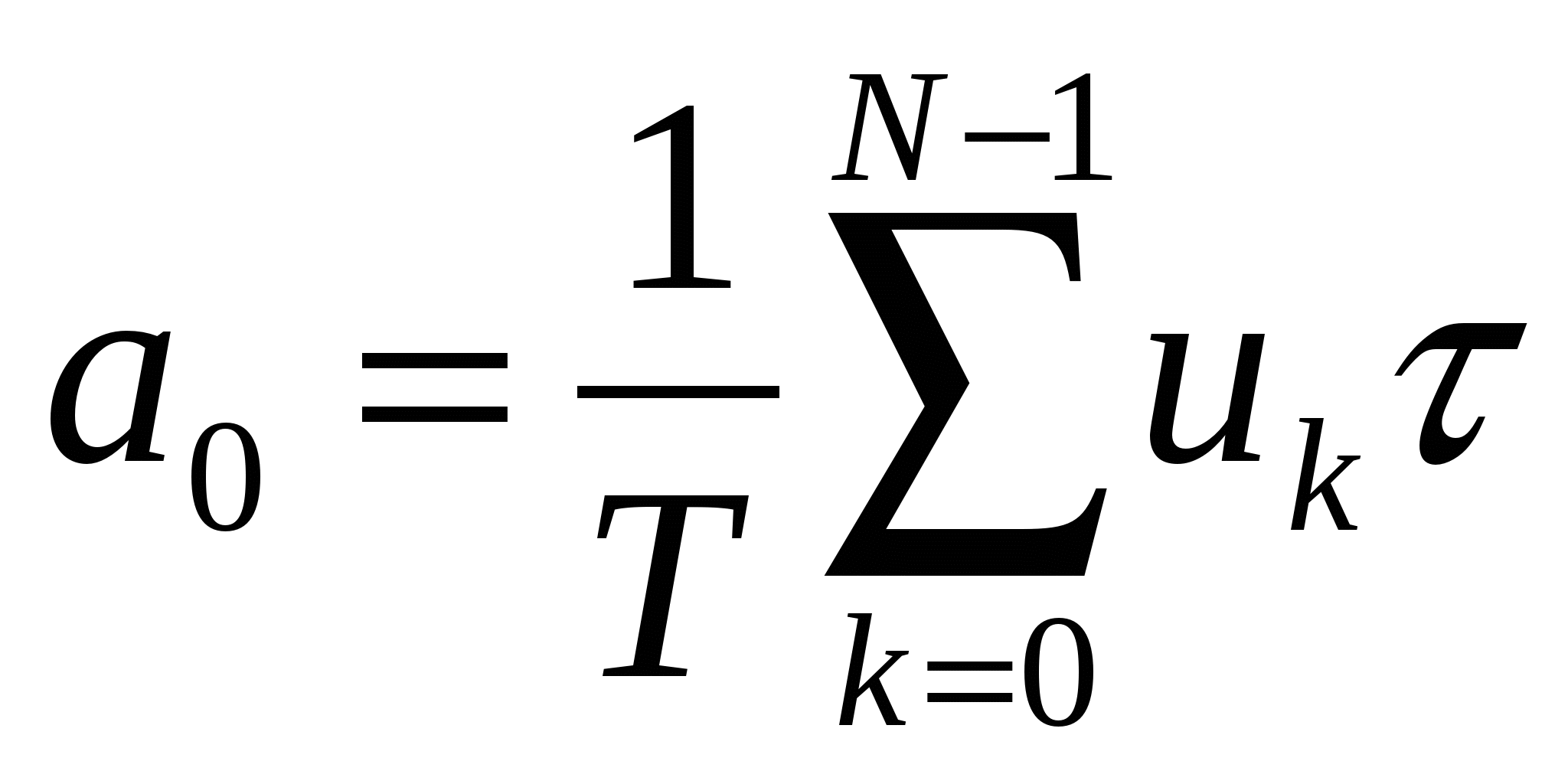,	(2.12)
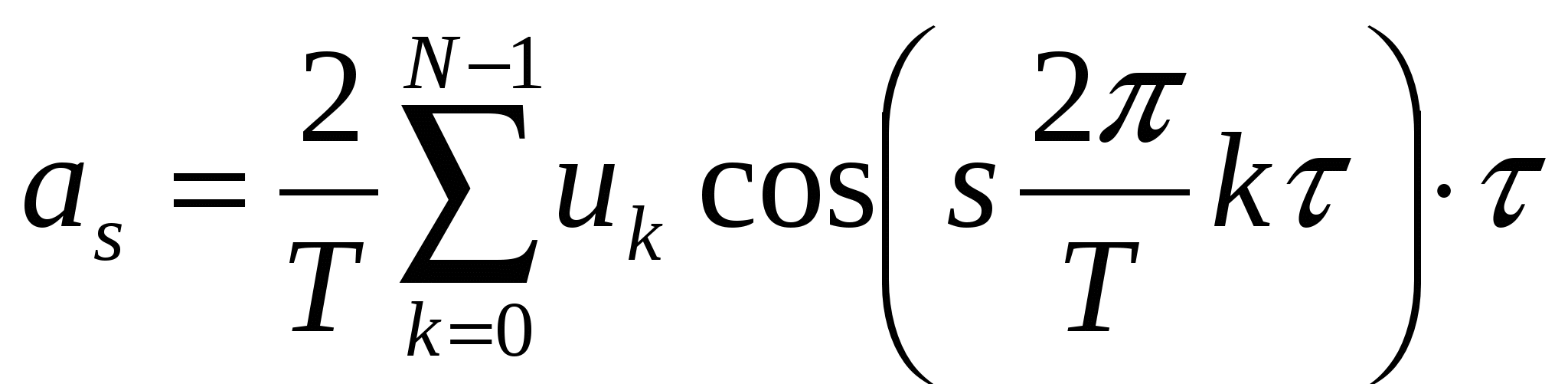,	(2.13)
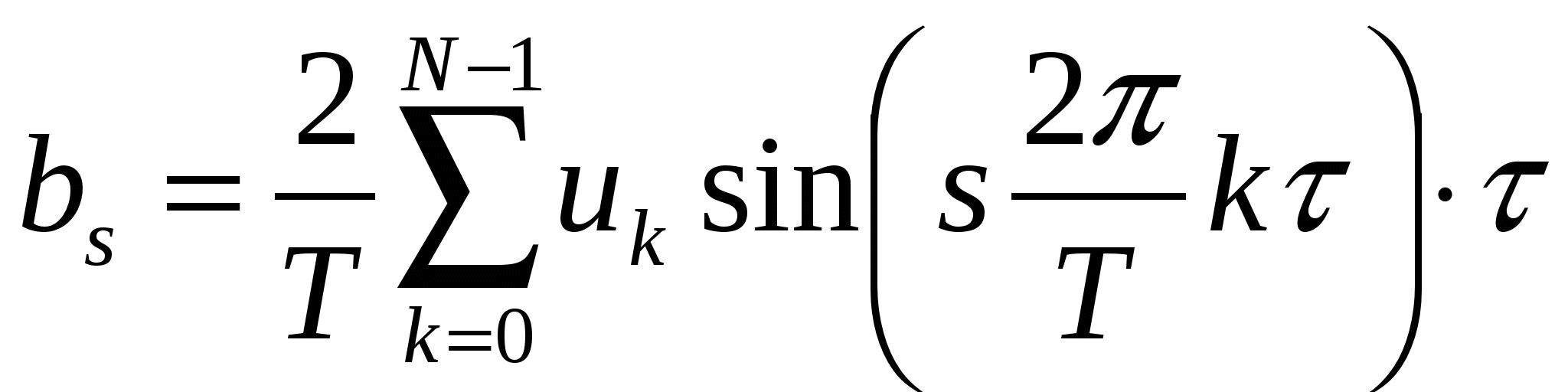.	(2.14)

В безразмерном виде основные формулы ДПФ имеют вид :

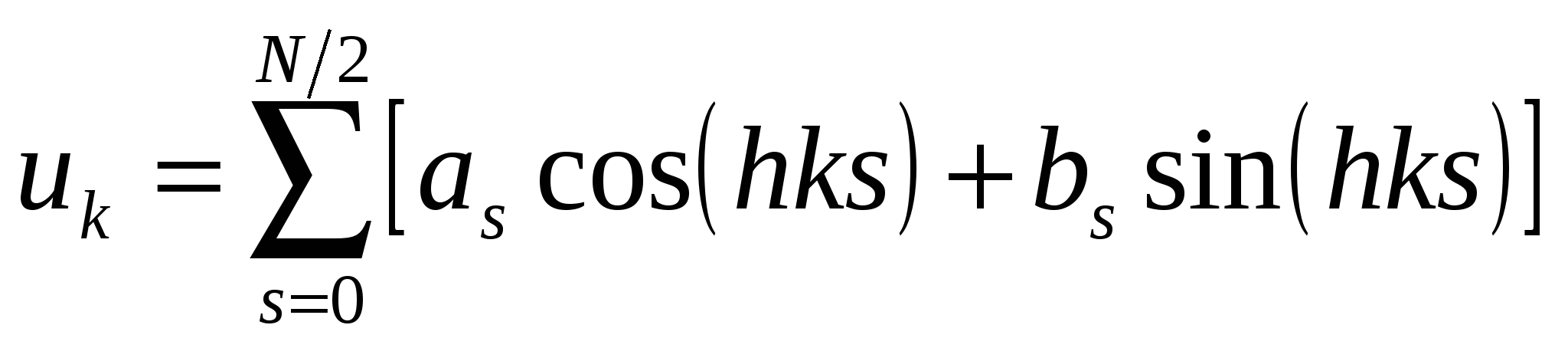
(2.15)

или

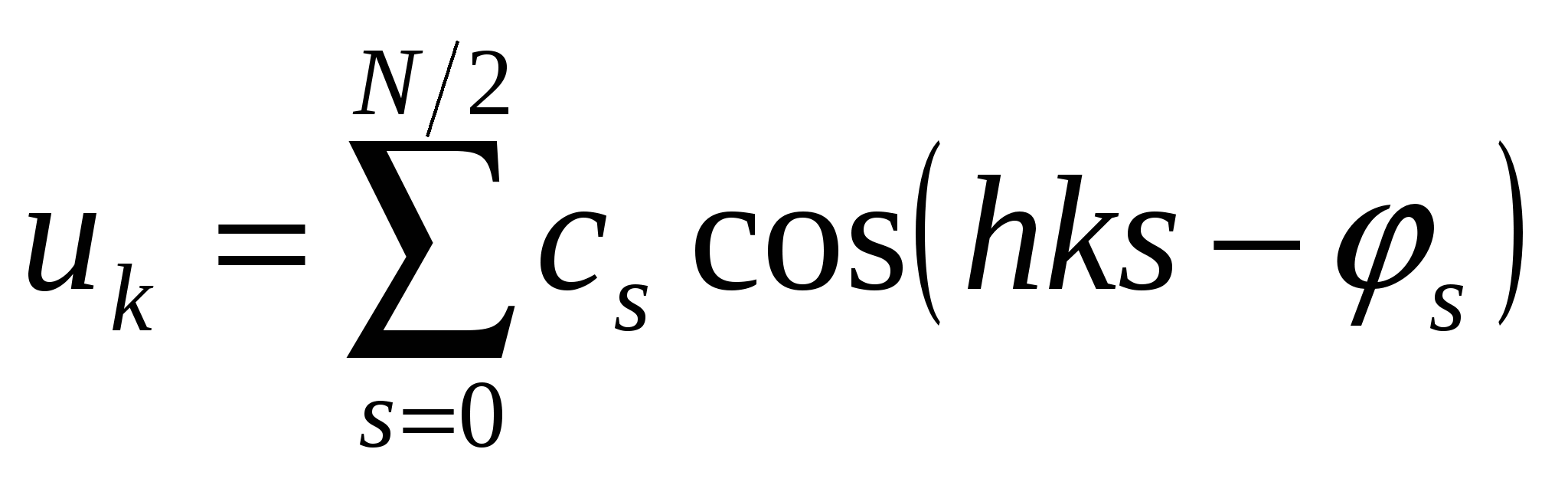
(2.16)

Формула (2.15) позволяет восстанавливать форму сигнала по его известному спектру и поэтому ее называют обратным ДПФ. Если же сигнал задан, т.е. известен массив 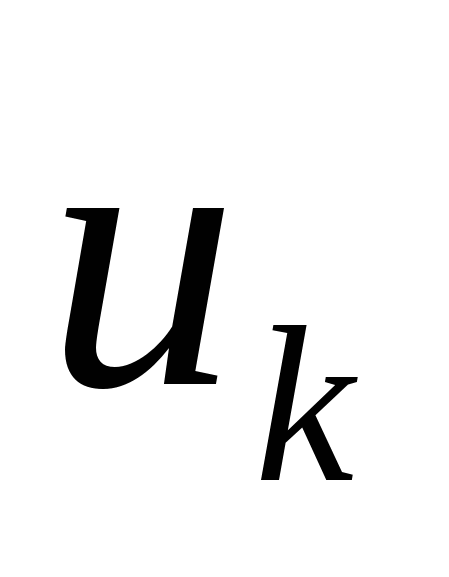и нужно определить его спектр, то применяется прямое ДПФ. Оно дает синусные и косинусные коэффициенты в (2.15) путем суммирования всех отсчетов сигнала.

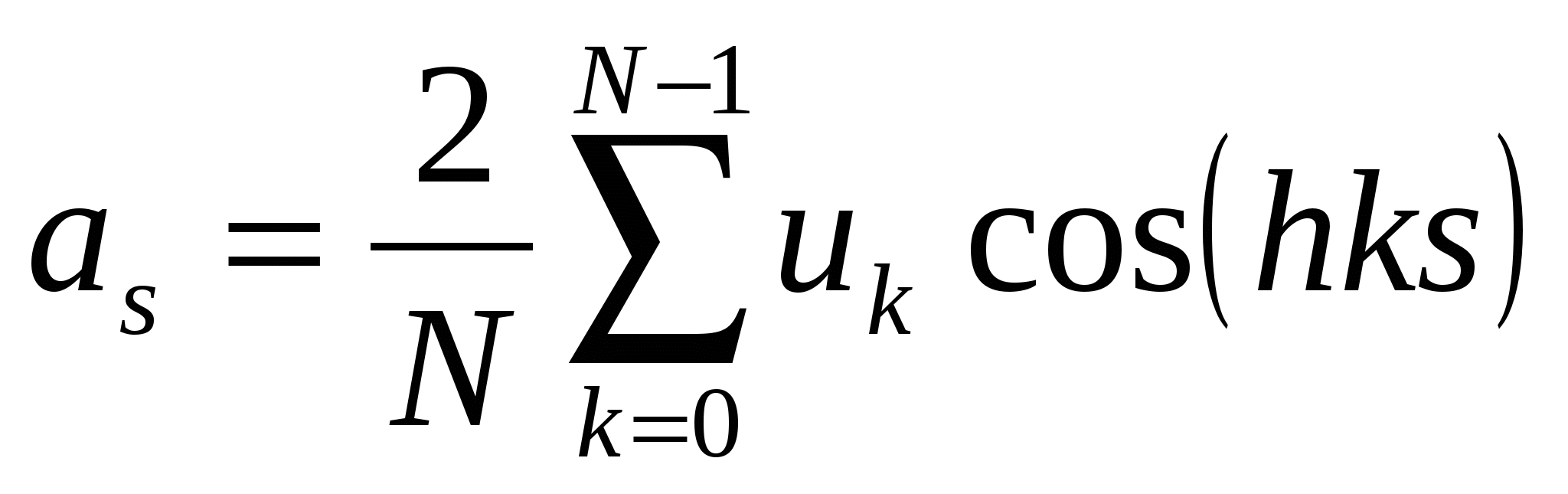
	(2.17)
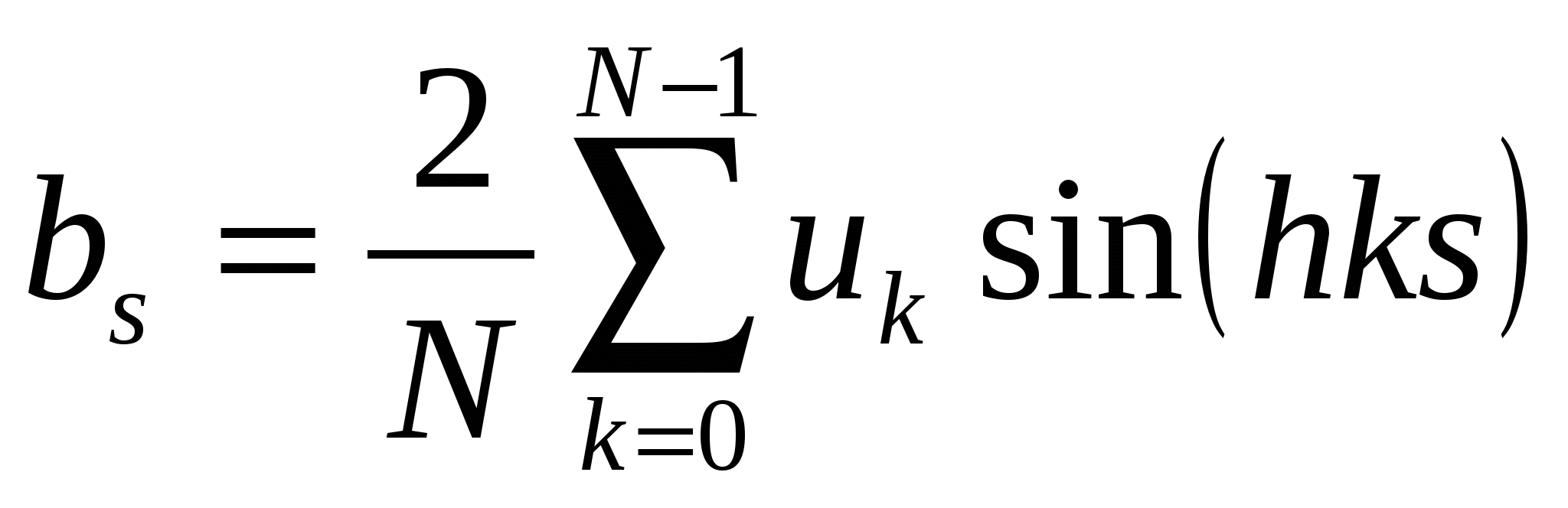
	(2.18)

Эти формулы применимы для гармоник с номерами 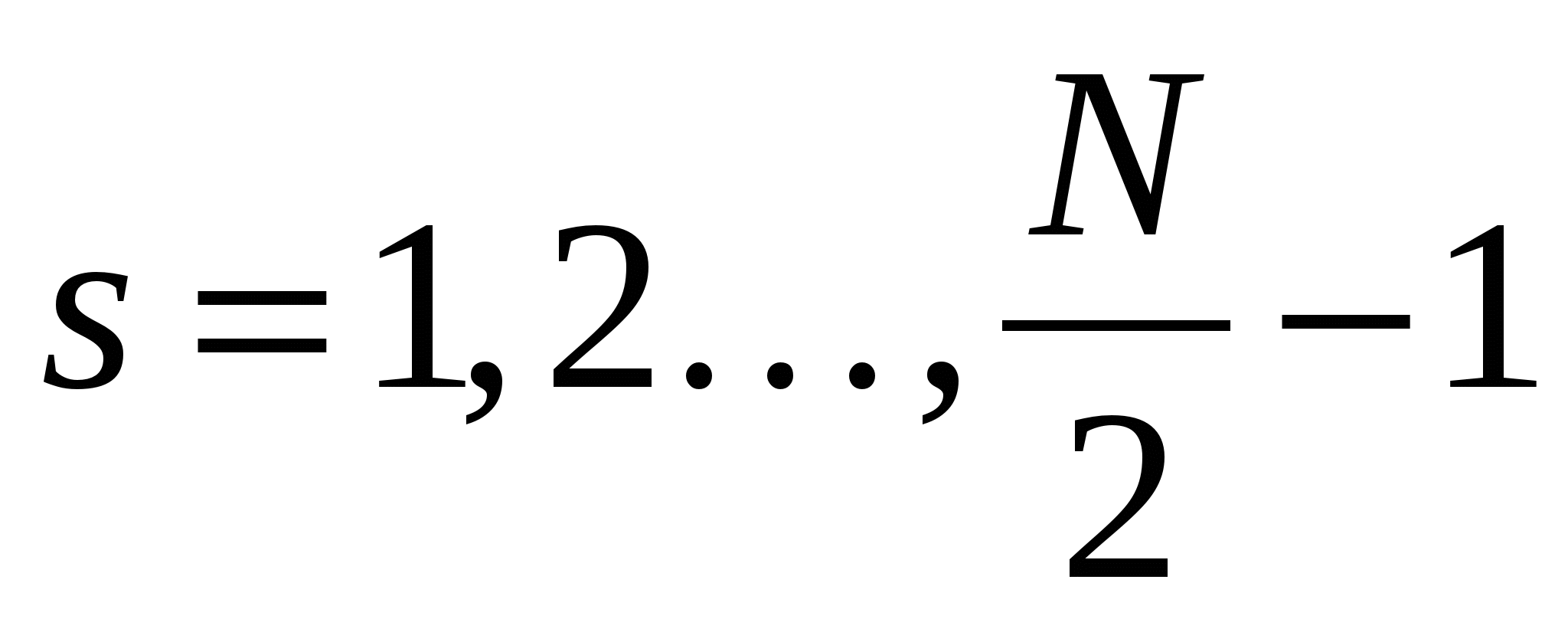, а для нулевой гармоники ( 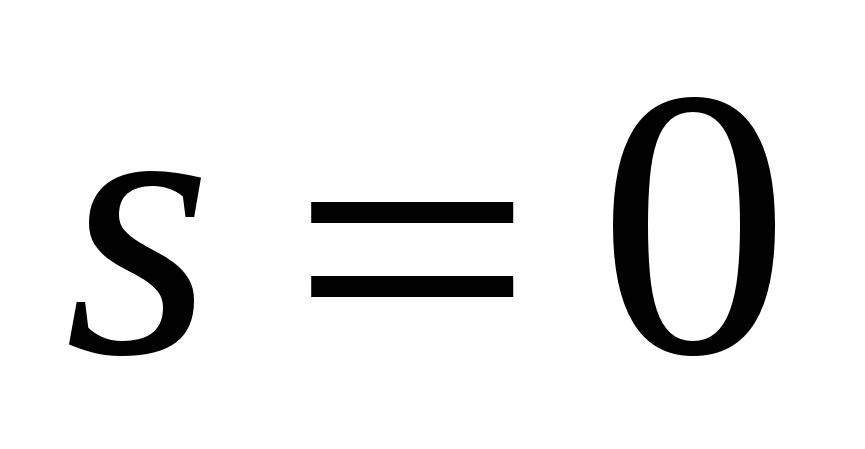) и последней 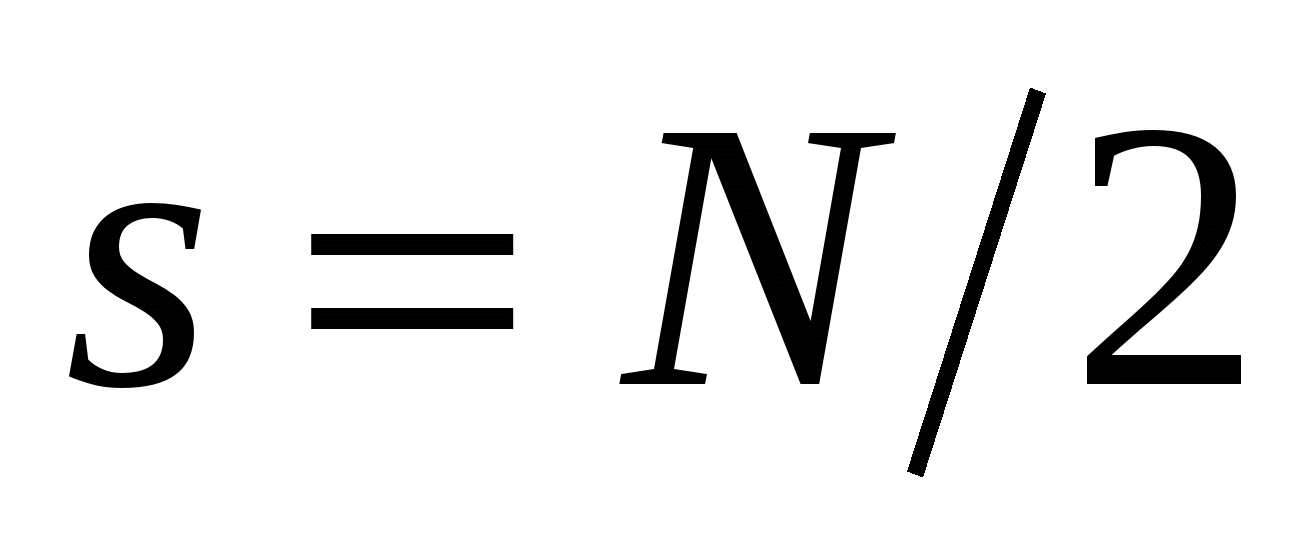в них нужно заменить коэффициент 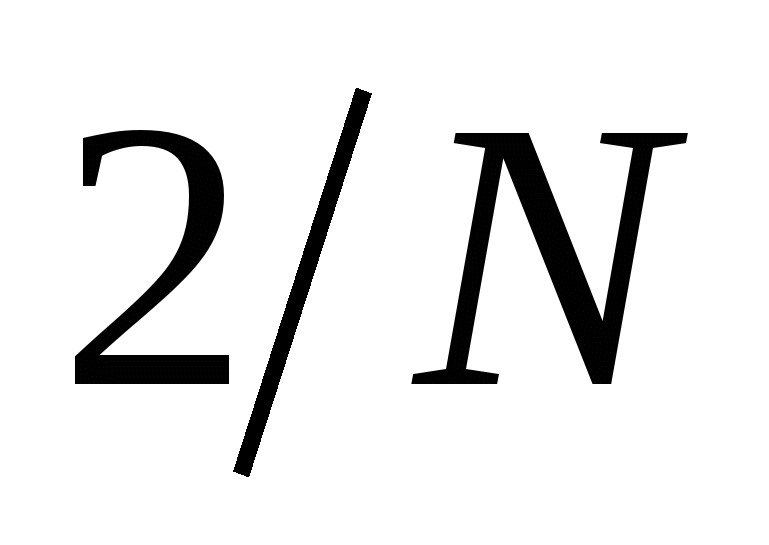на 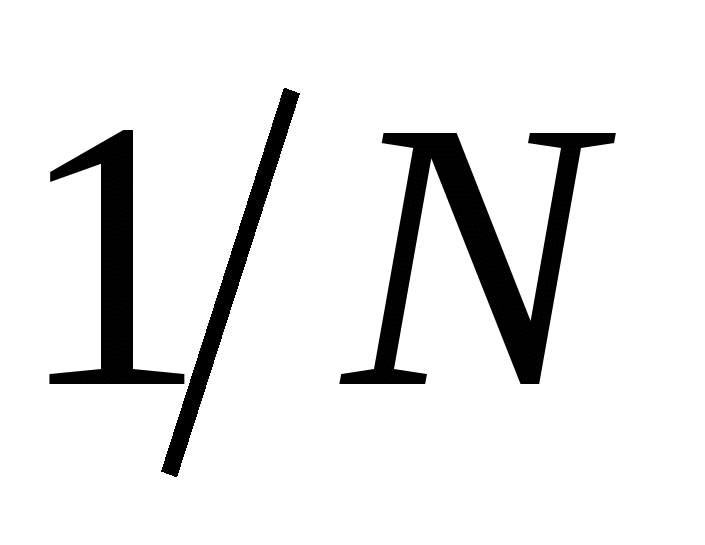. Из (2.18) следует, что и 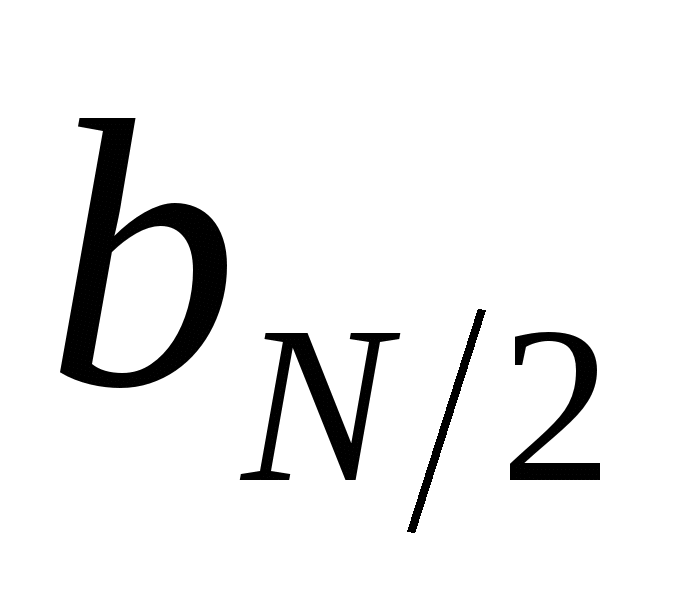произвольные, т.к. 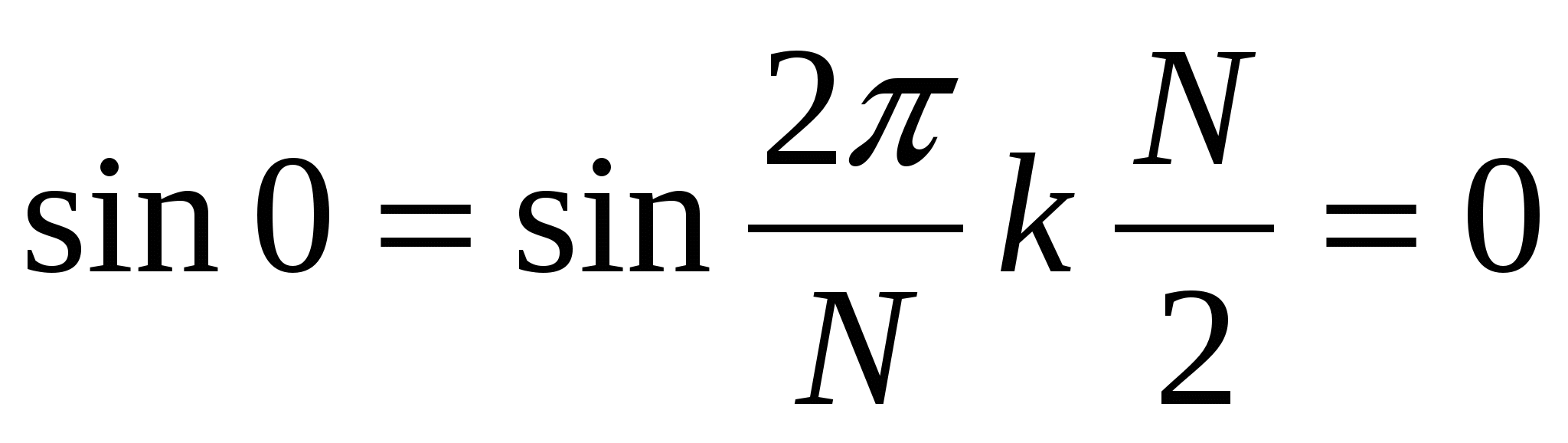Из (2.17) для нулевой и последней гармоник получаем

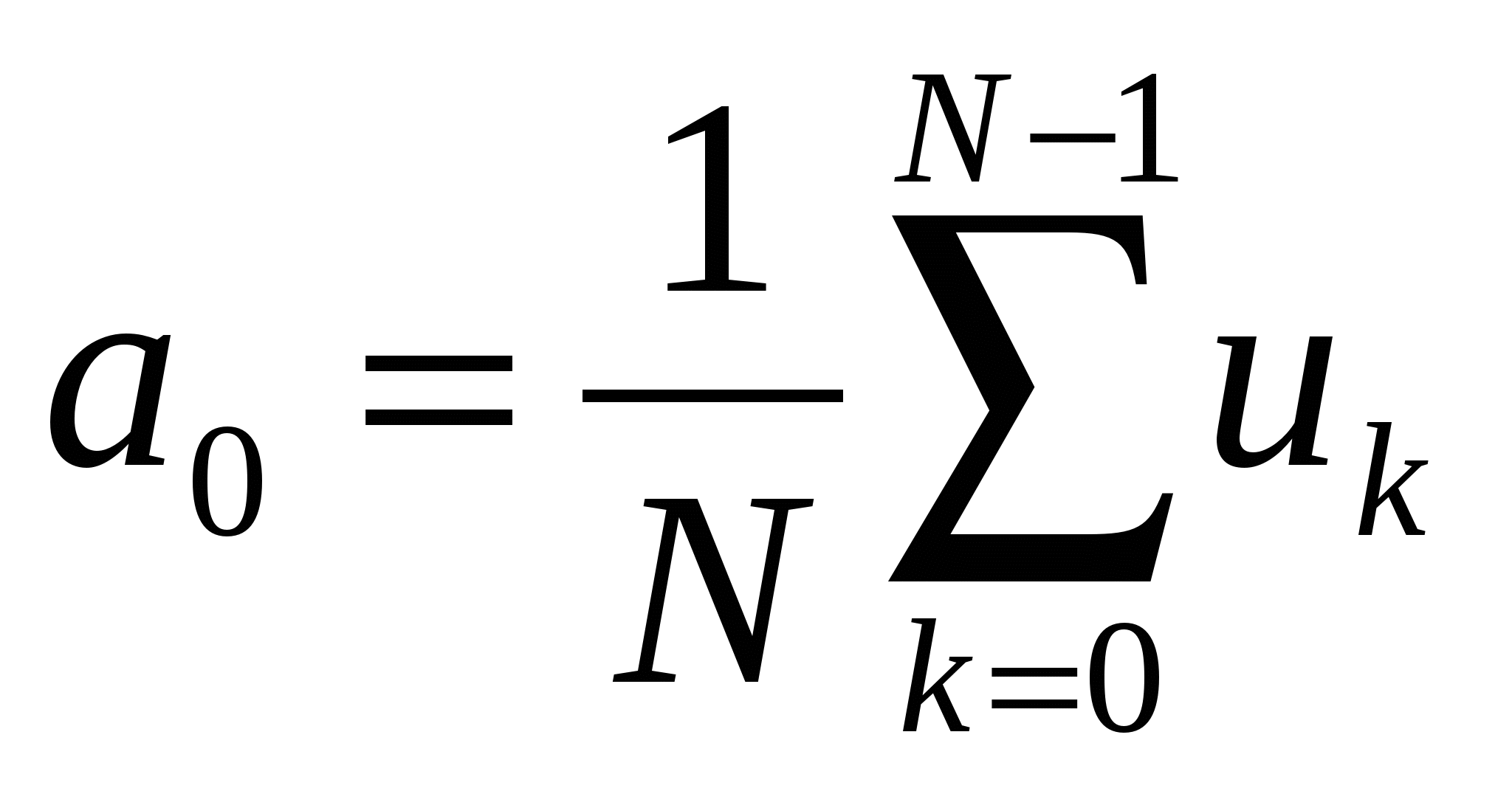,	(11.19)
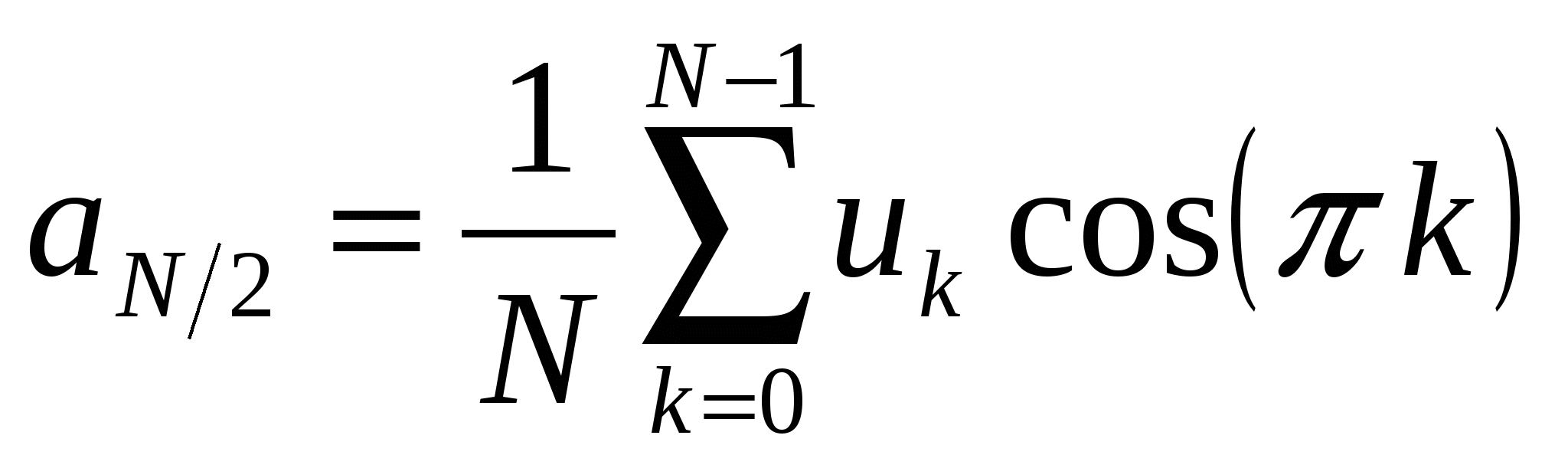
	(11.20)

Из (2.19) следует, что коэффициент 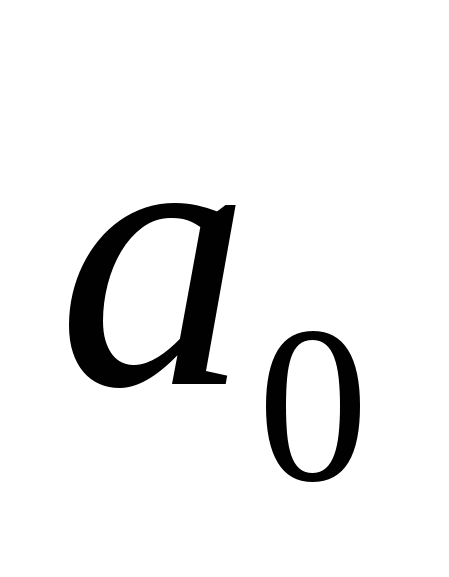определяет средний уровень сигнала на периоде, т.е. амплитуду постоянной составляющей .
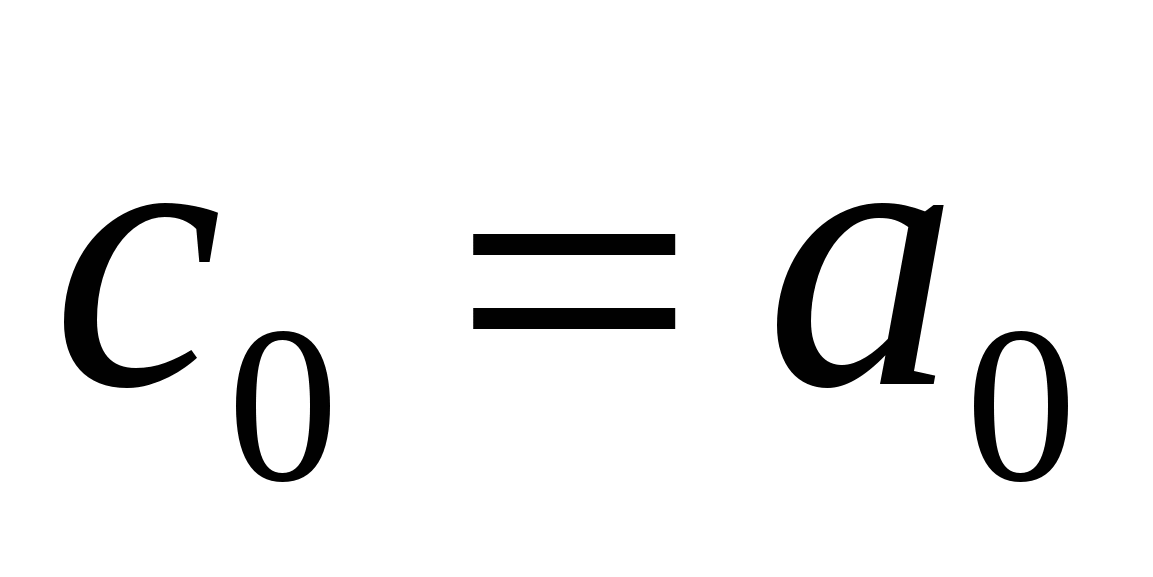Формулы (2.17), (2.18) можно пояснить также следующим образом. Суммирование произведений в них означает проверку ортогональности сигнала и гармонического колебания определенной частоты. Их ортогональность, соответствующая нулевым или малым коэффициентам 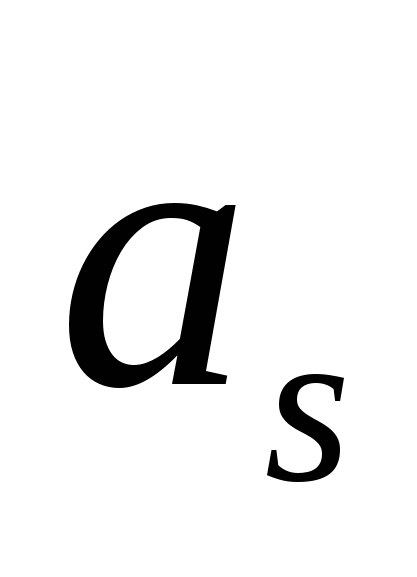и 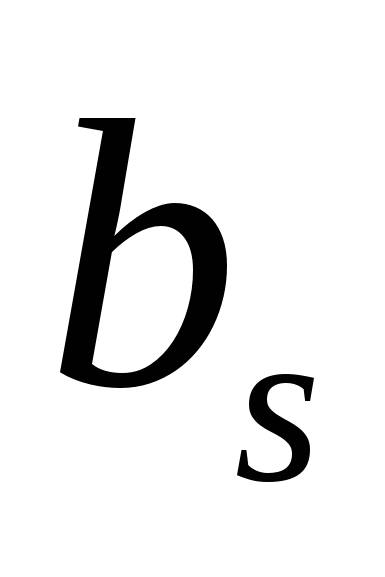означает, что они непохожи, т.е. таких колебаний нет в сигнале.