Наложение частот в ДПФ.
Этот эффект проявляется в тех случаях, когда количество отсчетов  сигнала на периоде выбрано недостаточно большим.
сигнала на периоде выбрано недостаточно большим.
Рассмотрим произвольный аналоговый сигнал 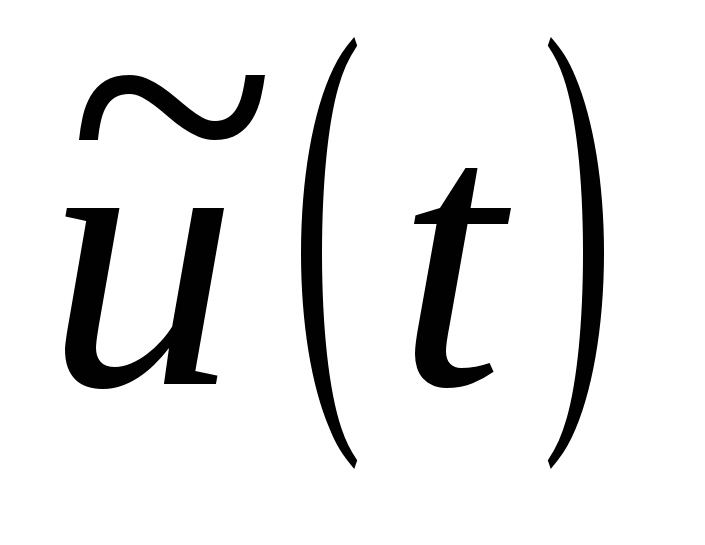 . Пусть
. Пусть 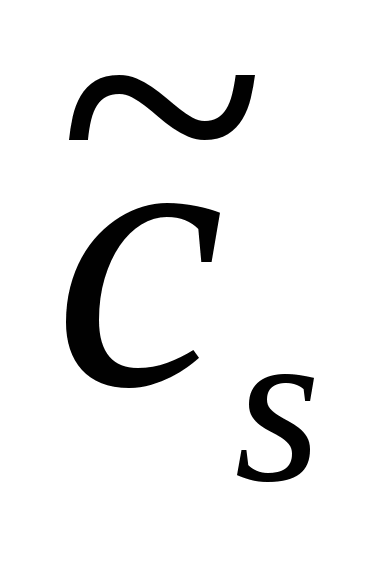 - его амплитудный спектр, который в общем случае содержит бесконечное количество гармоник. Пусть рассматриваемый сигнал дискретизирован и по
- его амплитудный спектр, который в общем случае содержит бесконечное количество гармоник. Пусть рассматриваемый сигнал дискретизирован и по  его точкам с помощью ДПФ вычислен спектр
его точкам с помощью ДПФ вычислен спектр 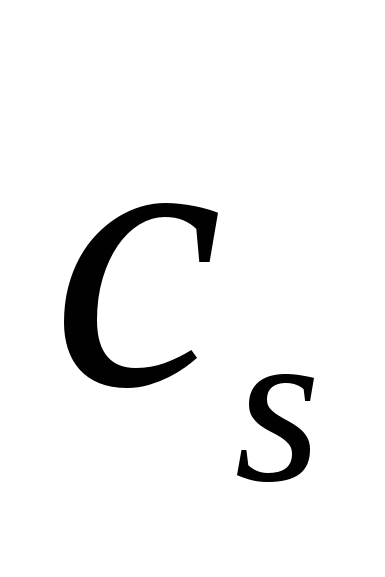 , содержащий
, содержащий 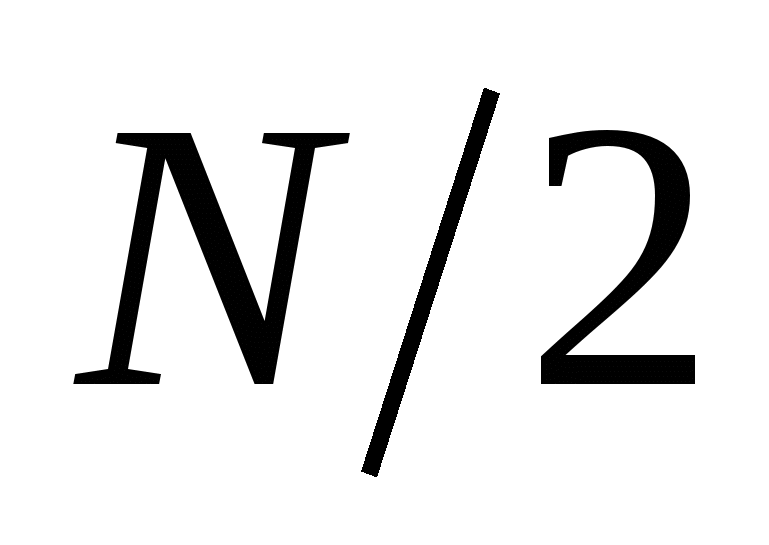 гармоник.
гармоник.
Если значение N выбрано правильно, то спектры 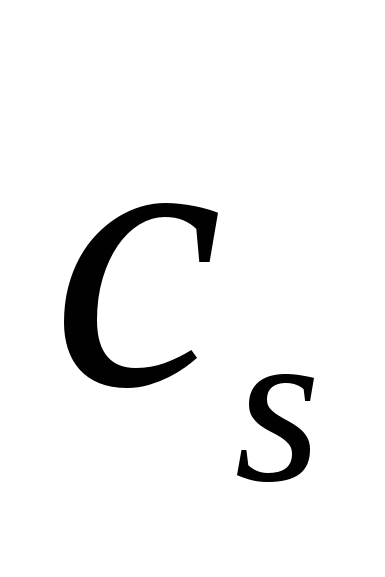 и
и 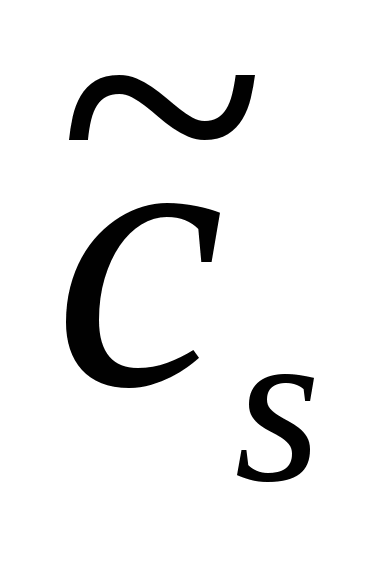 совпадают. Если же
совпадают. Если же  недостаточно велико, то спектры
недостаточно велико, то спектры 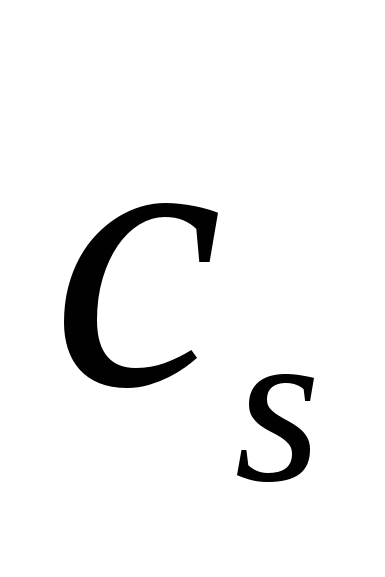 и
и 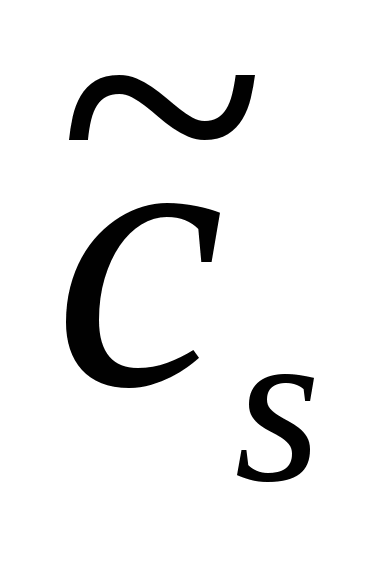 существенно различаются, что показано на рис.2.4.
существенно различаются, что показано на рис.2.4.
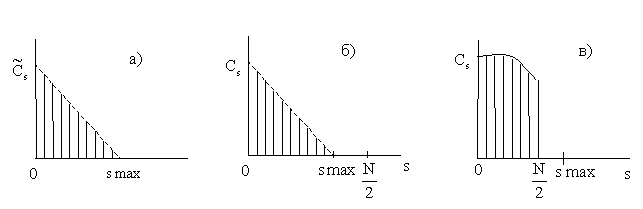
|
Рис. 2.4. Спектры аналогового и дискретного сигнала при правильном (б) и неправильном (в) выборе значения  . .
|
На рис.2.4в даны только гармоники для рабочего диапазона ДПФ 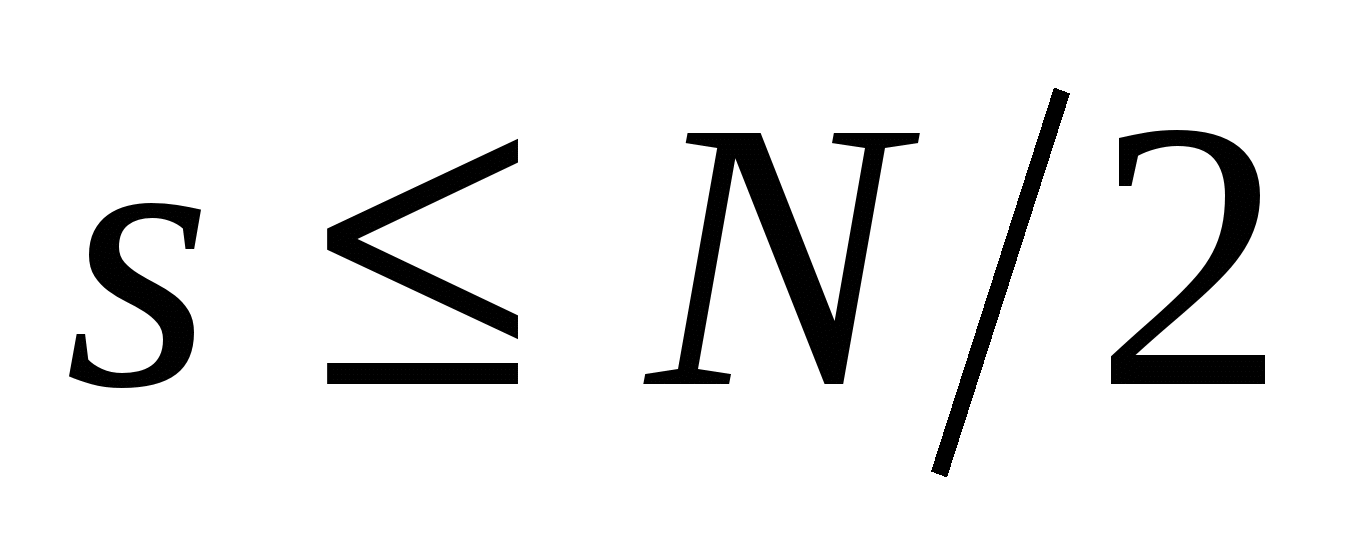 , а далее эти гармоники повторяются в соответствии с рис.2.3. Большие погрешности в спектре рис.2.1в обусловлены тем, что в исходном аналоговом сигнале есть гармоники с номерами
, а далее эти гармоники повторяются в соответствии с рис.2.3. Большие погрешности в спектре рис.2.1в обусловлены тем, что в исходном аналоговом сигнале есть гармоники с номерами 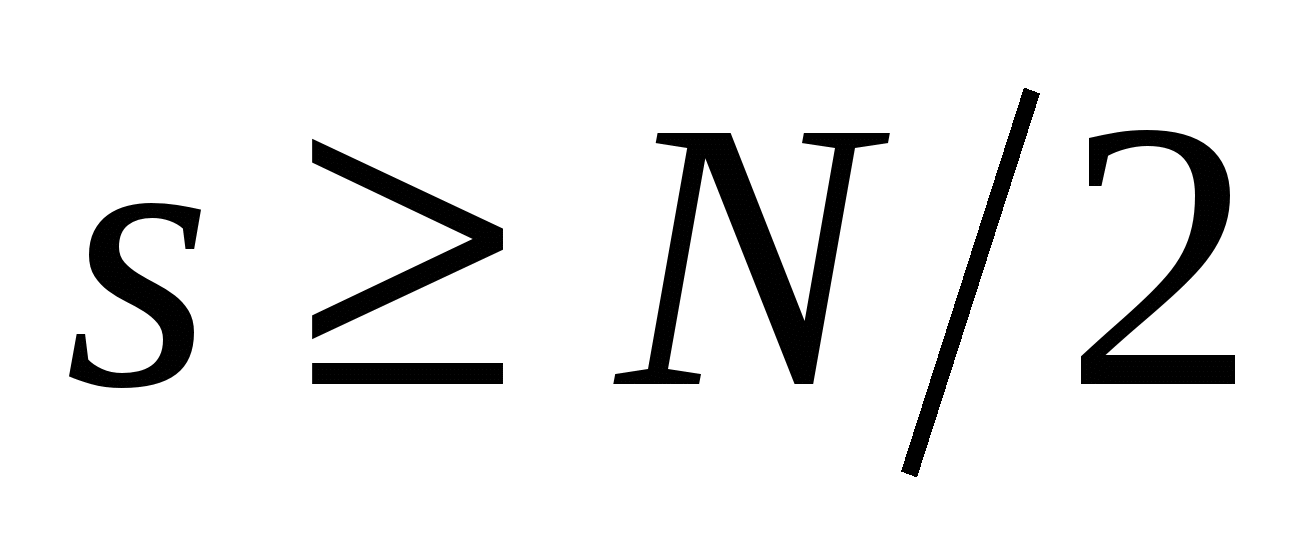 , а в ДПФ они не рассматриваются из-за периодичности спектра.
, а в ДПФ они не рассматриваются из-за периодичности спектра.
Пусть 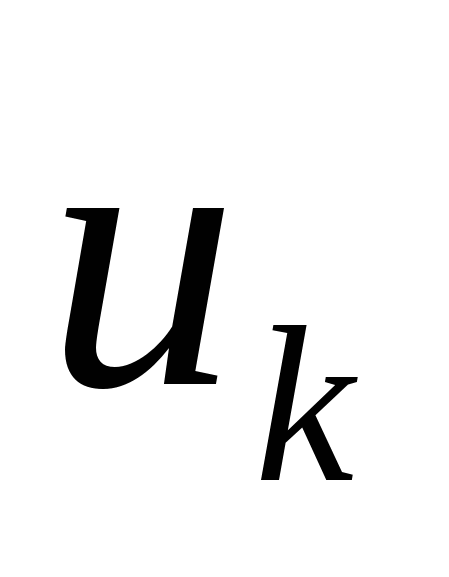 - отсчет исходного аналогового сигнала
- отсчет исходного аналогового сигнала 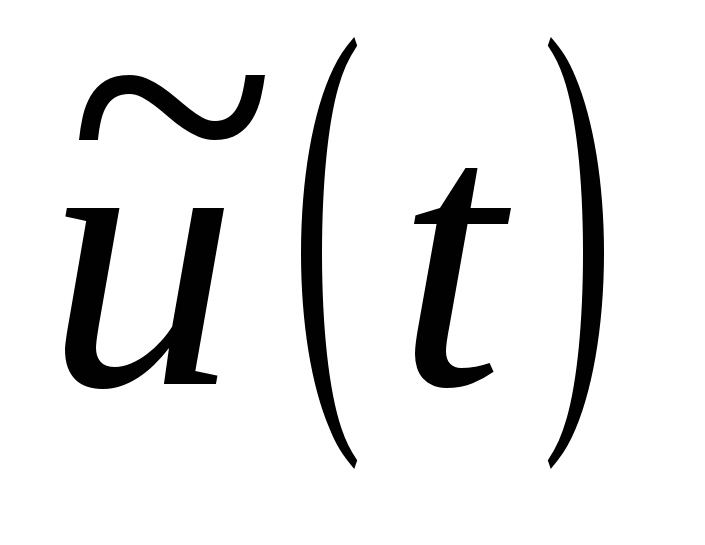 , т.е.
, т.е. 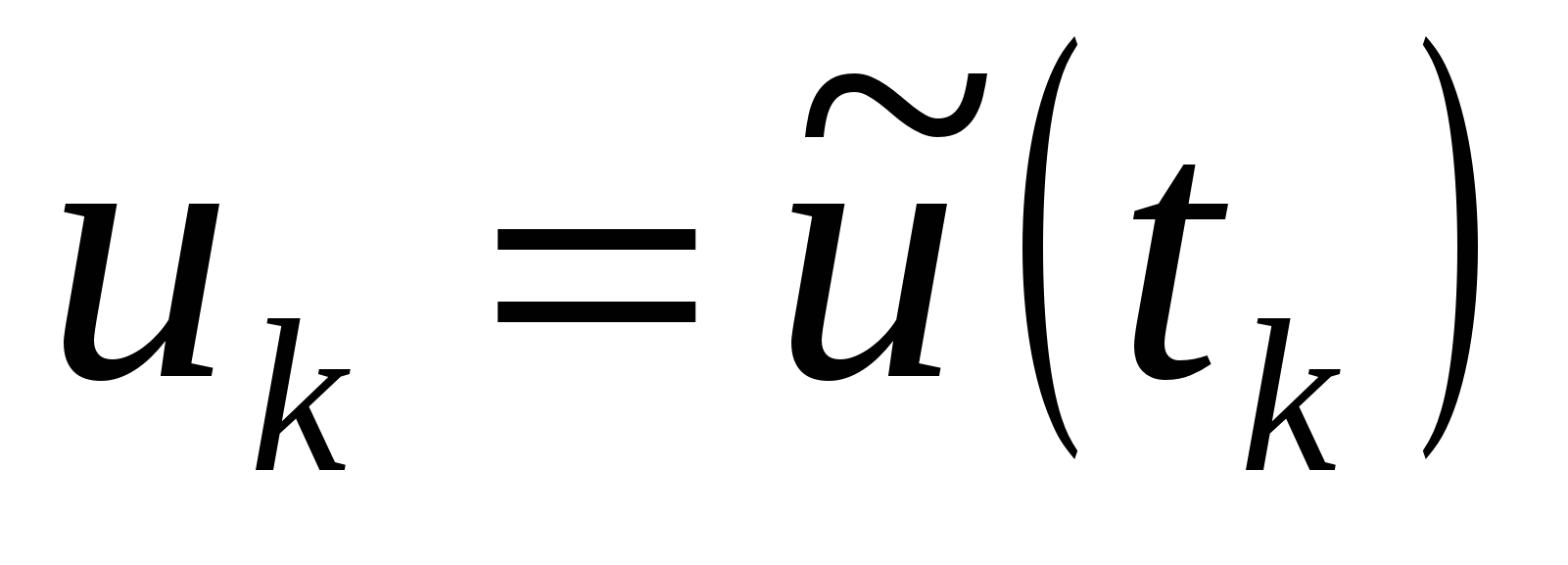 ,
, 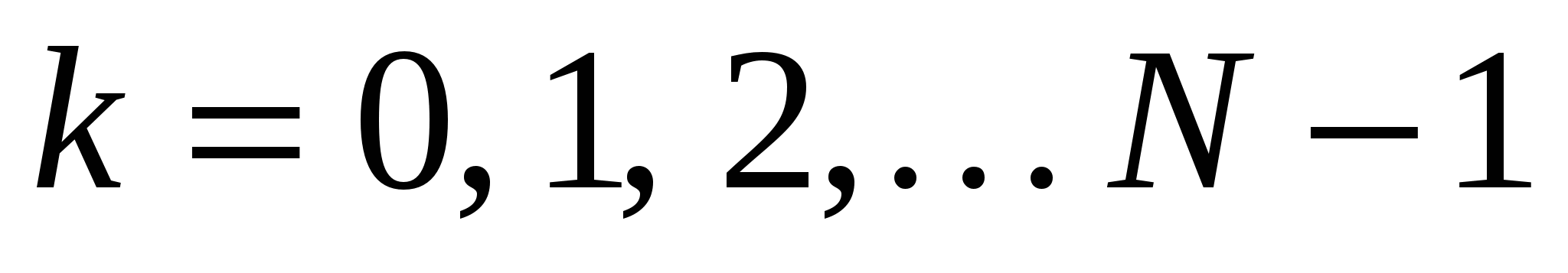 .
.
Далее знак суммы по 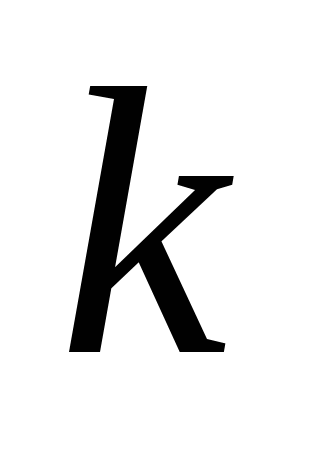 будет означать суммирование по этим значением
будет означать суммирование по этим значением 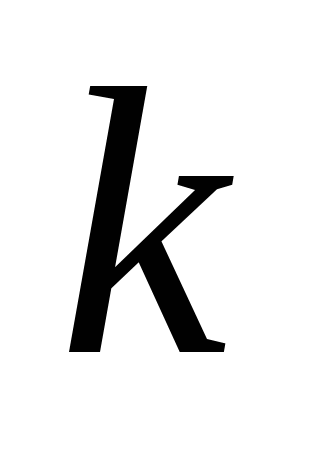 , т.е. по всем отсчетам. Используем целый индекс
, т.е. по всем отсчетам. Используем целый индекс 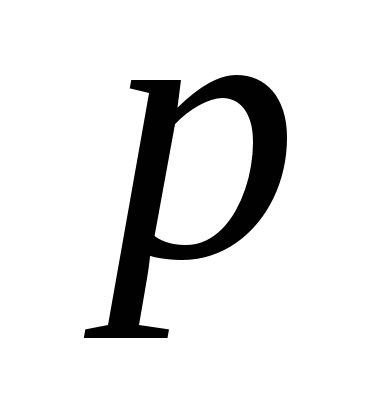 для гармоник аналогового сигнала,
для гармоник аналогового сигнала, 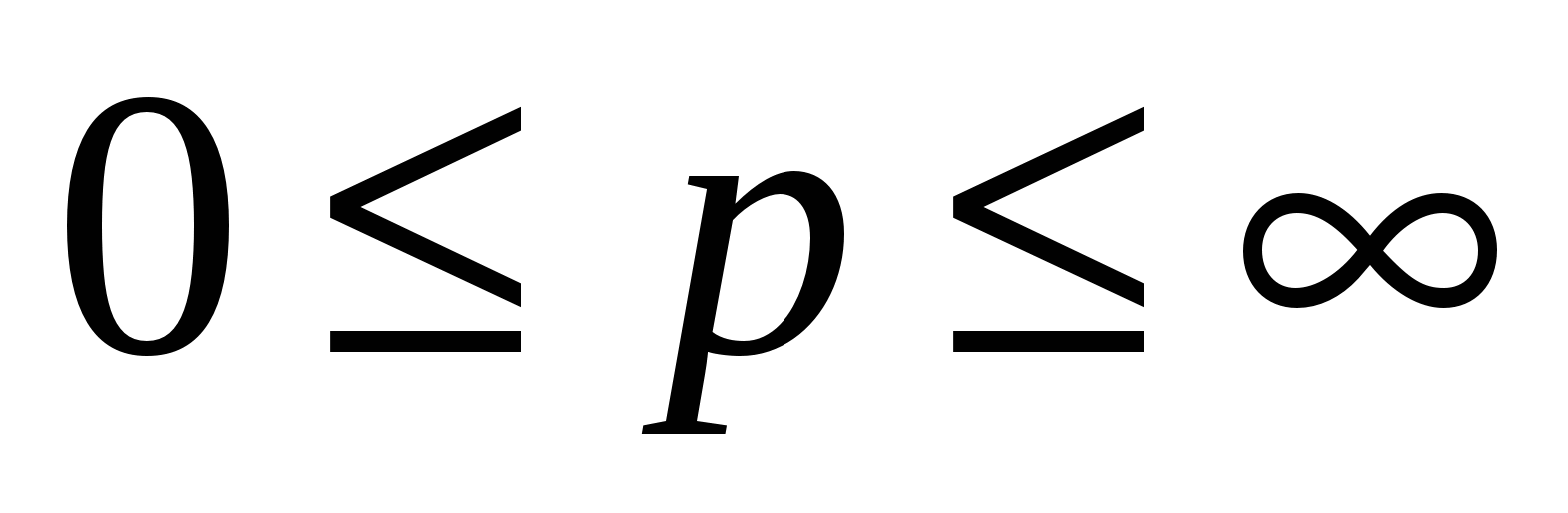 в общем случае. Тогда аналоговое преобразование Фурье (АПФ) можно записать в соответствии с (2.2) в виде
в общем случае. Тогда аналоговое преобразование Фурье (АПФ) можно записать в соответствии с (2.2) в виде

| (2.24) |
По отсчетам (2.24) вычисляем прямое ДПФ, т.е. подставляем (2.24) в (2.17) или (2.19). Получим двойную сумму вида
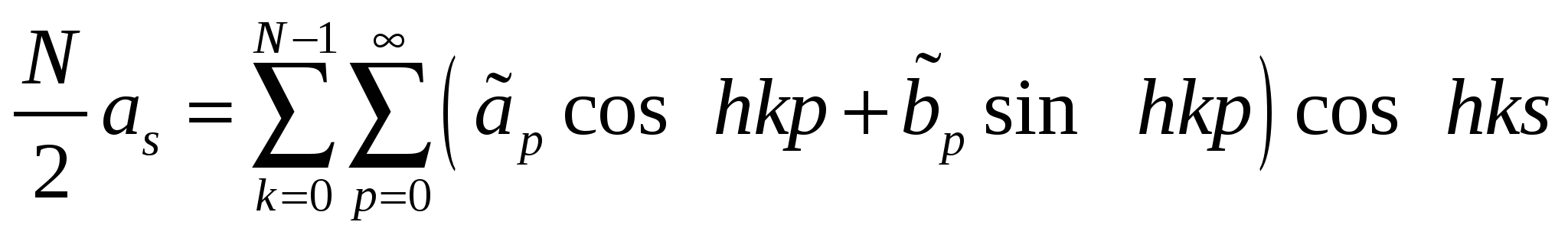
| (2.25) |
Раскроем скобки и используем известные формулы для произведений, например,
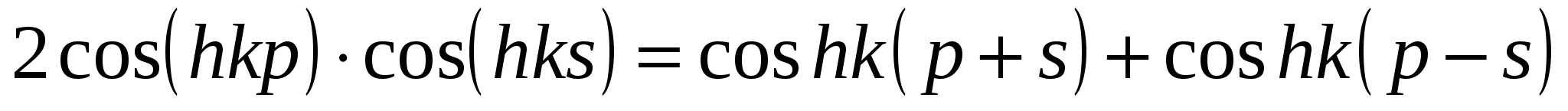
Можно показать, что
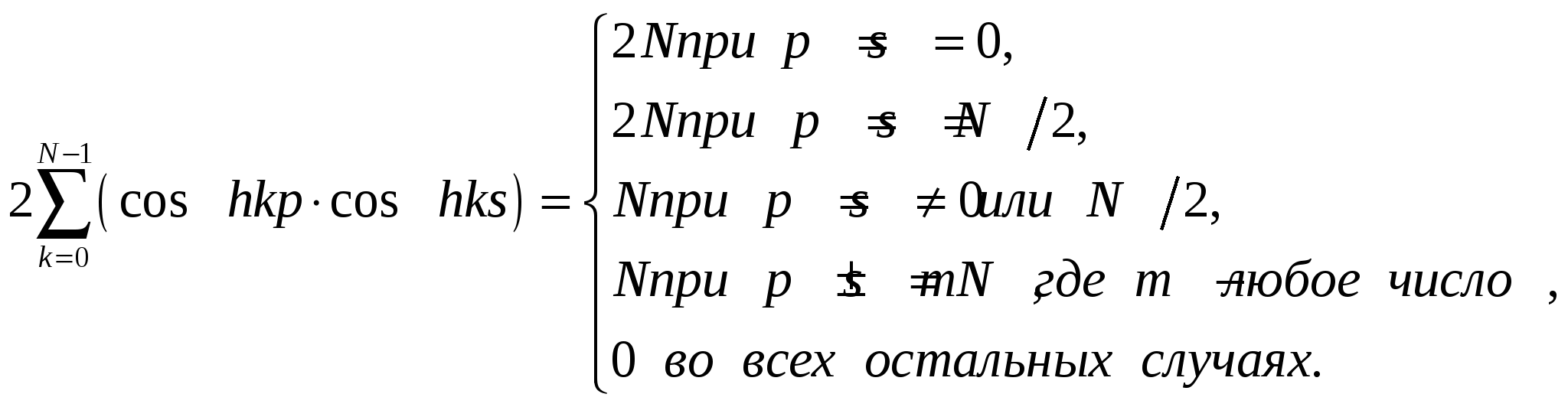
При этом учитывается, что 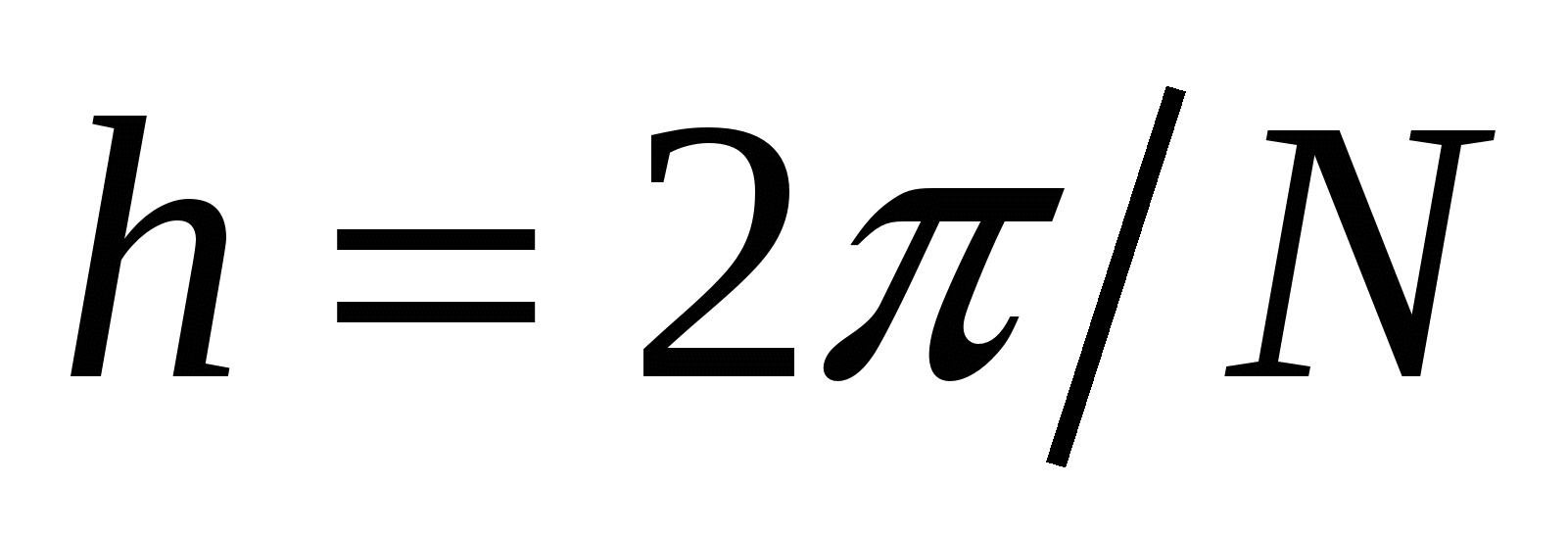
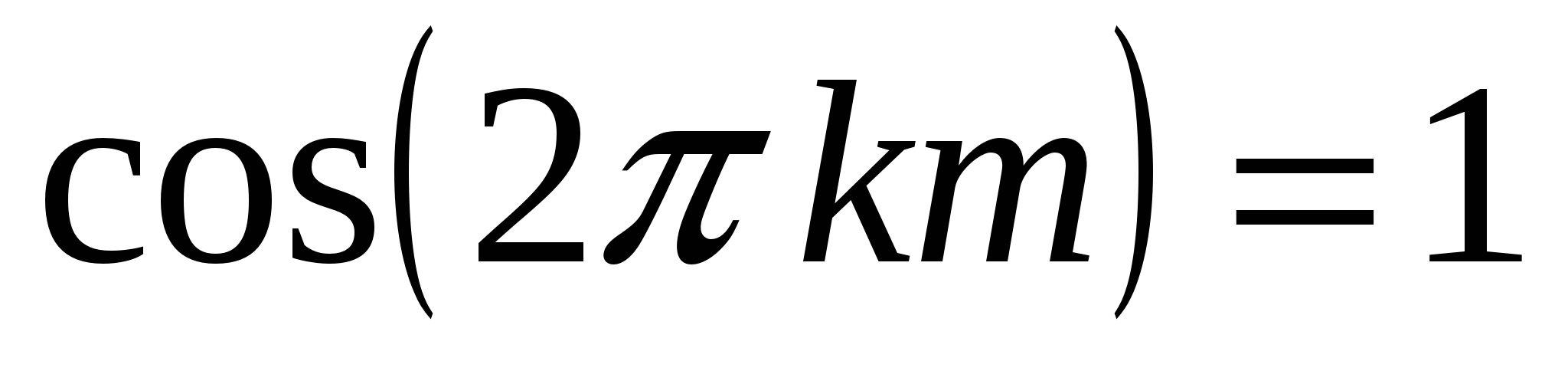 . Поэтому для коэффициента
. Поэтому для коэффициента 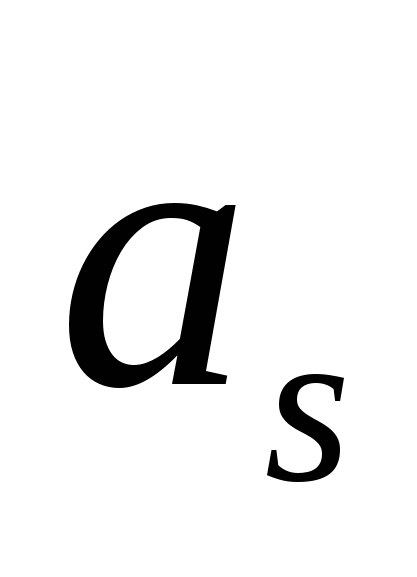 (или
(или 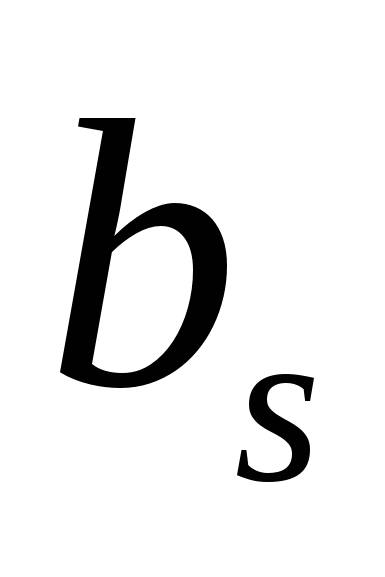 ) большинство слагаемых в двойной сумме (2.25) по k и p будет равно нулю и останутся только слагаемые с
) большинство слагаемых в двойной сумме (2.25) по k и p будет равно нулю и останутся только слагаемые с 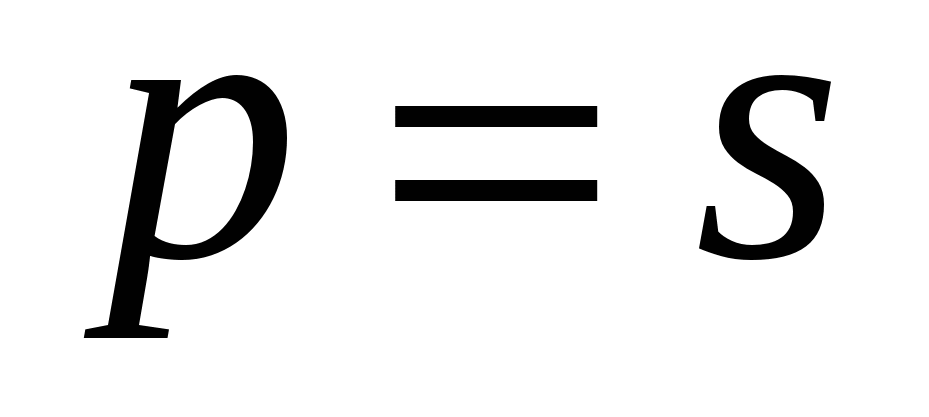 и слагаемые, для которых
и слагаемые, для которых 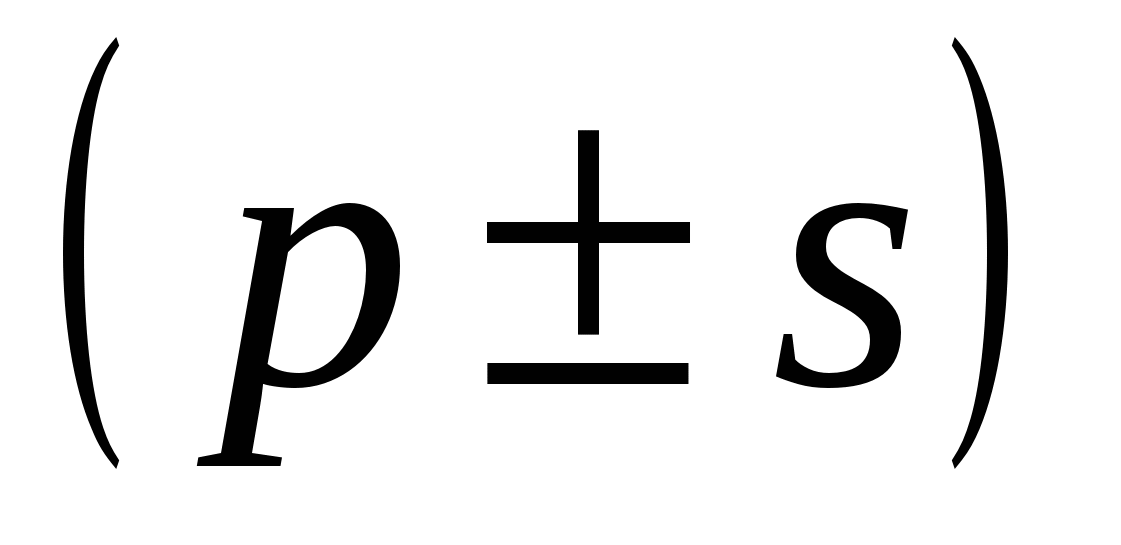 кратно
кратно  .
.
Если аккуратно провести все указанные преобразования, то из (2.25) получим
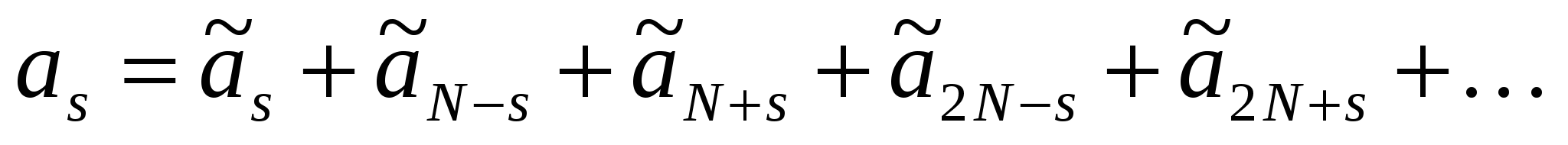
| (2.26) |
и аналогичную формулу для 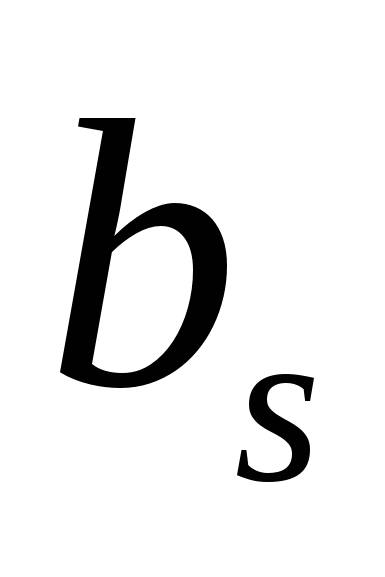 . Из (2.26) делаем следующие выводы:
. Из (2.26) делаем следующие выводы:
1. В вещественном ДПФ вычисляются гармоники с номерами 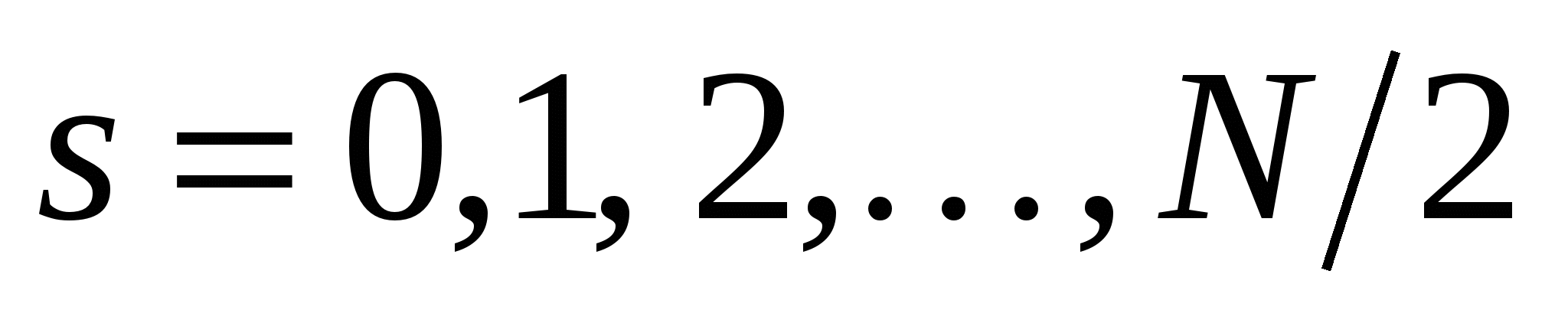 , хотя в исходном аналоговом сигнале могут присутствовать гармоники с номерами
, хотя в исходном аналоговом сигнале могут присутствовать гармоники с номерами 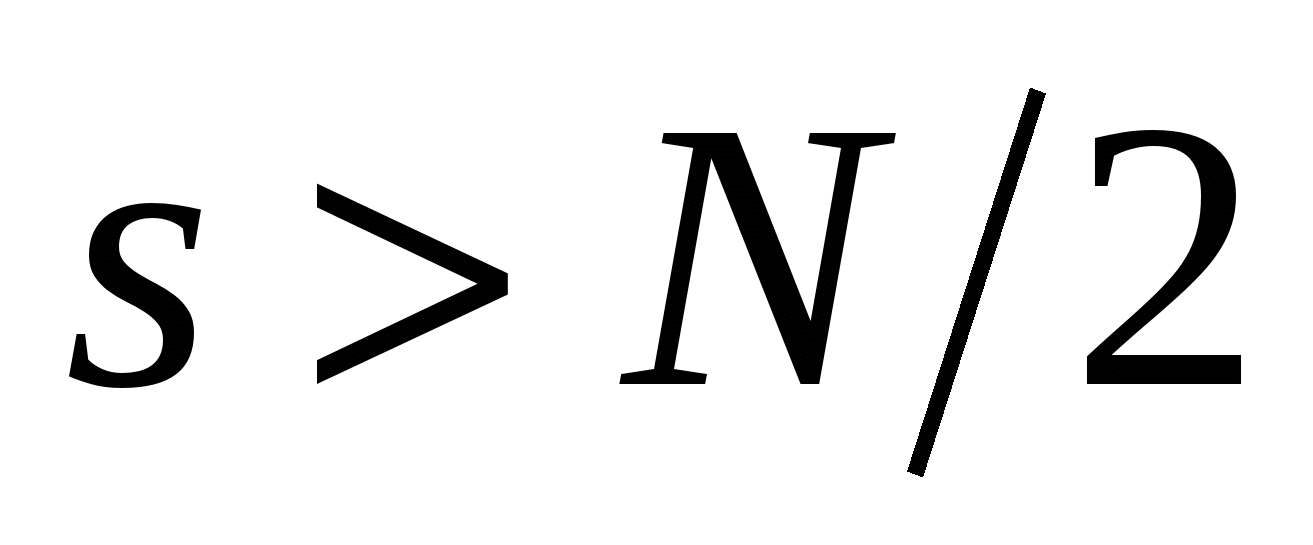 .
.
2. Если в спектре исходного аналогового сигнала есть гармоники с номерами 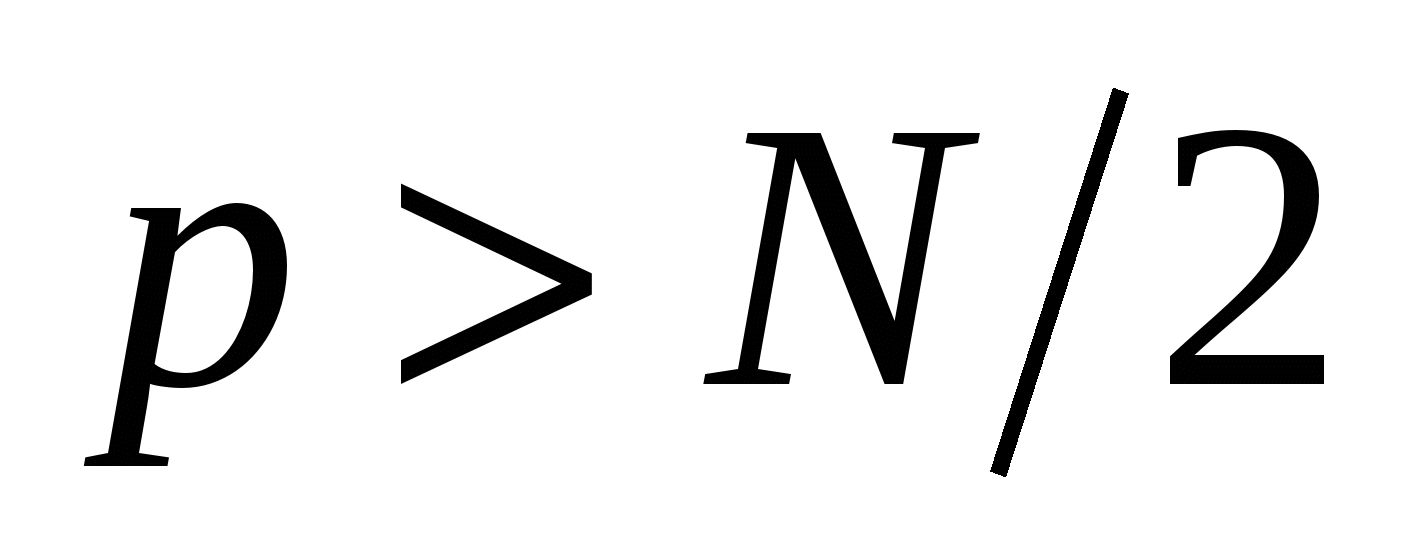 то при вычислении ДПФ они накладываются на гармоники с номерами
то при вычислении ДПФ они накладываются на гармоники с номерами 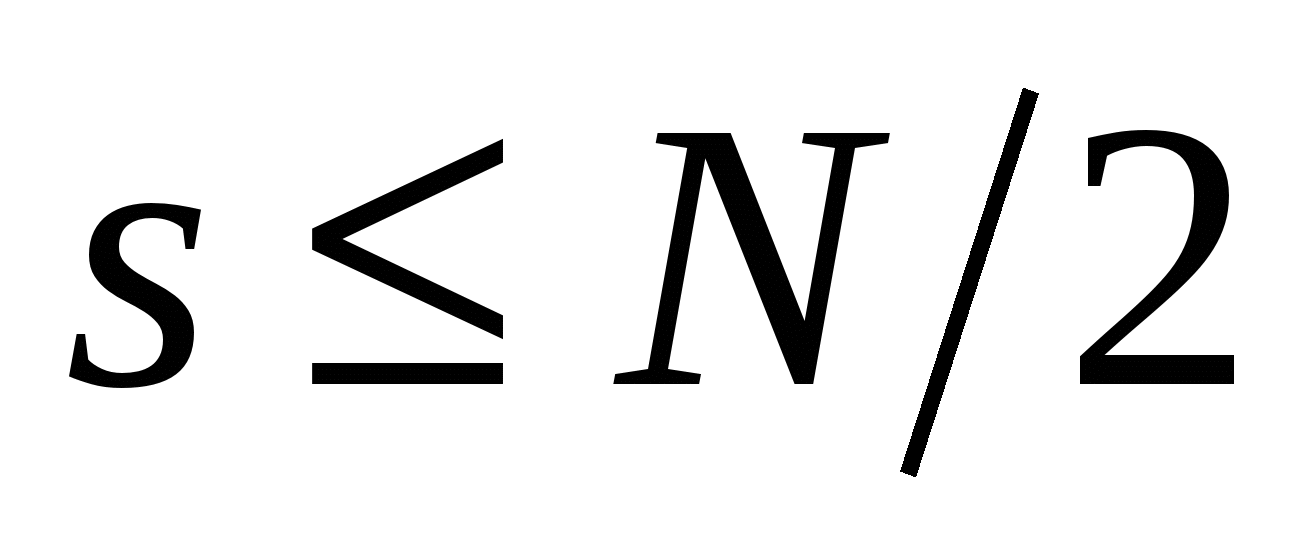 и искажают их. Наложение происходит для гармоник с номерами
и искажают их. Наложение происходит для гармоник с номерами 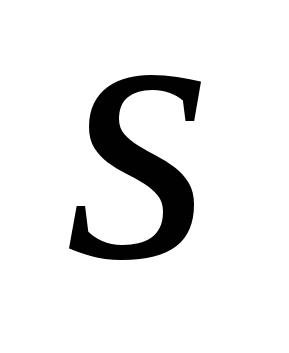 и
и 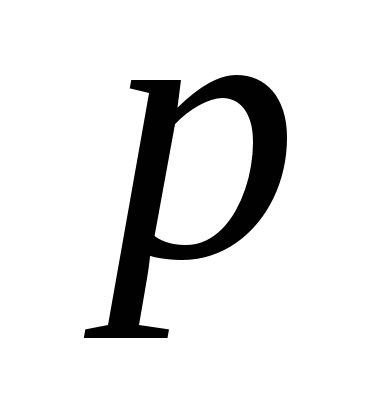 , если
, если 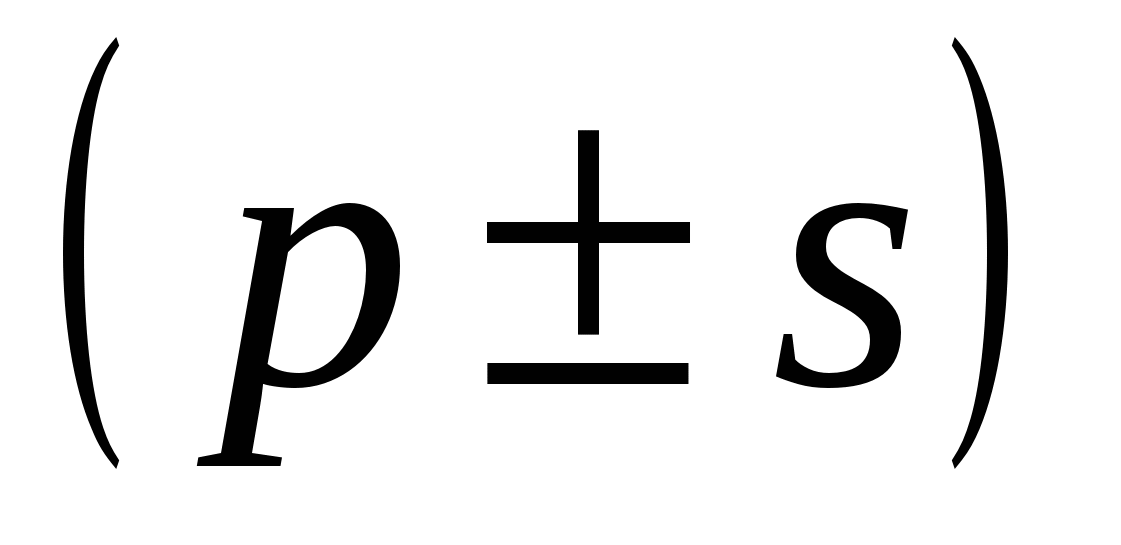 кратно
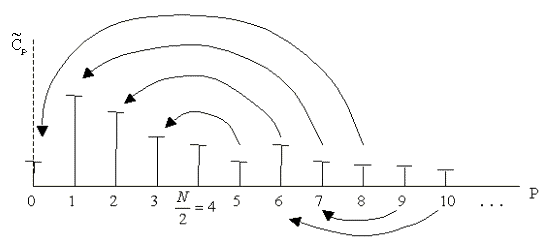
кратно  . Это и есть эффект наложения частот (см. рис.2.5). При этом исходный спектр складывается как бы "гармошкой".
. Это и есть эффект наложения частот (см. рис.2.5). При этом исходный спектр складывается как бы "гармошкой".
|
Рис.2.5. Эффект наложения частот при ДПФ. 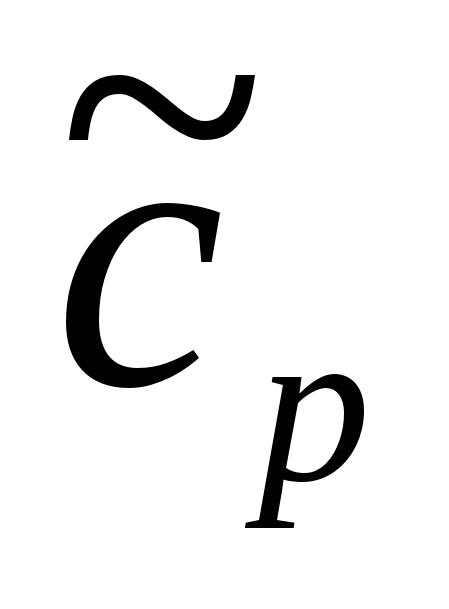 - амплитудный спектр аналогового сигнала; здесь для ДПФ - амплитудный спектр аналогового сигнала; здесь для ДПФ 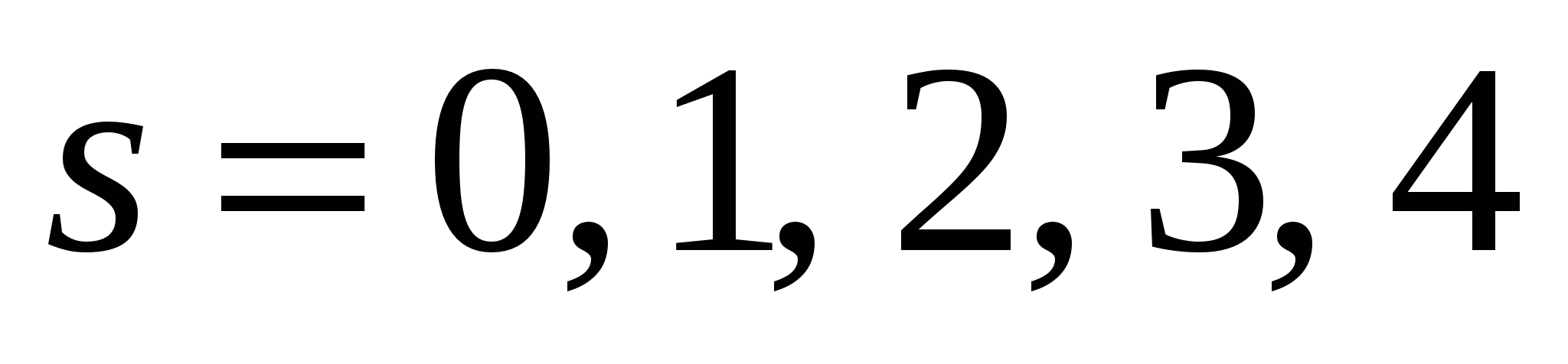 , т.к. , т.к. 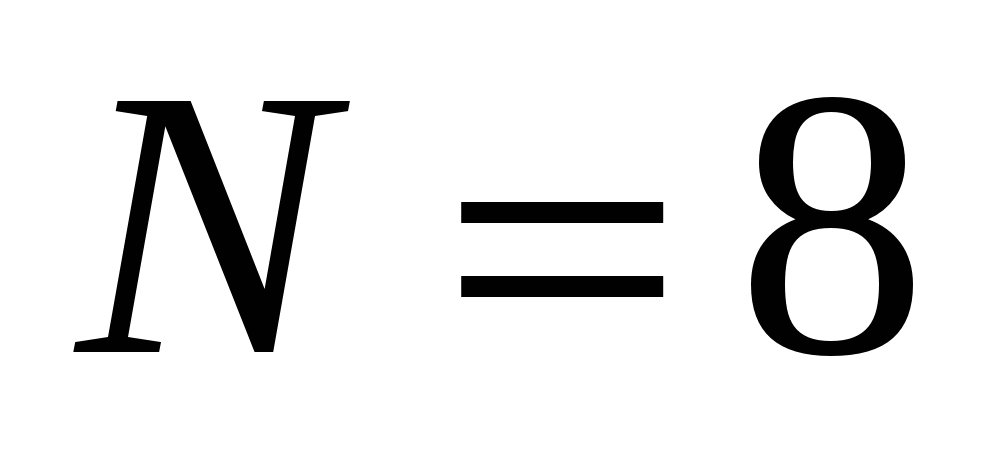 . .
|
3. Для устранения эффекта наложения частот нужны фильтры верхних частот для аналогового сигнала или большие значения N, т.к. спектр аналогового сигнала не должен иметь гармоник с номерами 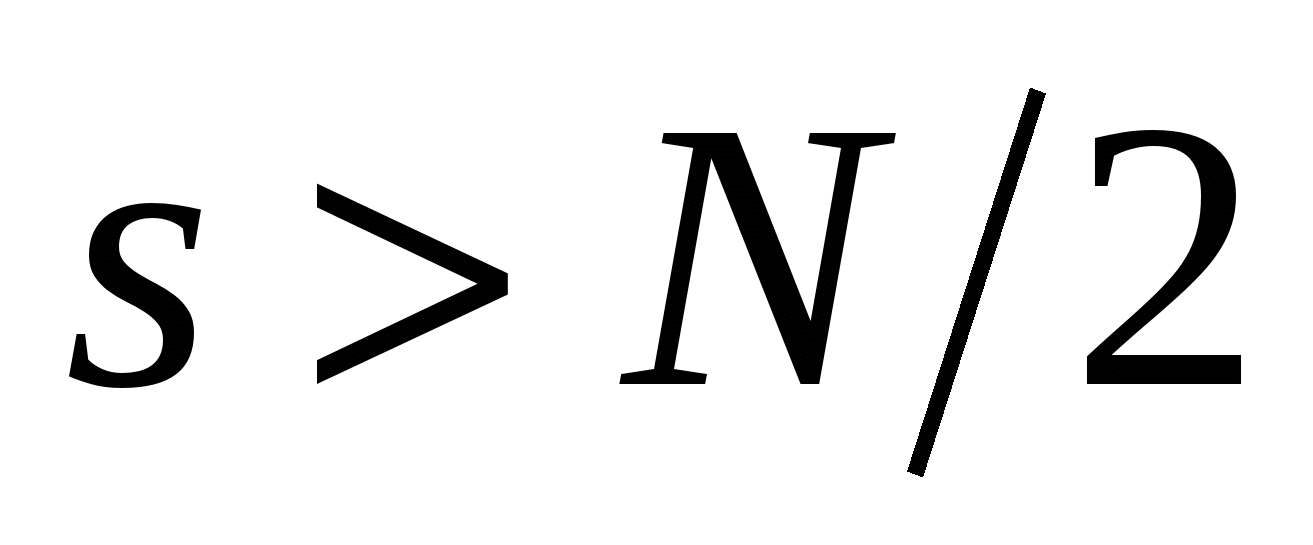 . Если такие гармоники есть, то они не должны превышать заданной погрешности вычисления спектра.
. Если такие гармоники есть, то они не должны превышать заданной погрешности вычисления спектра.
Пример. Пусть в аналоговом сигнале имеем 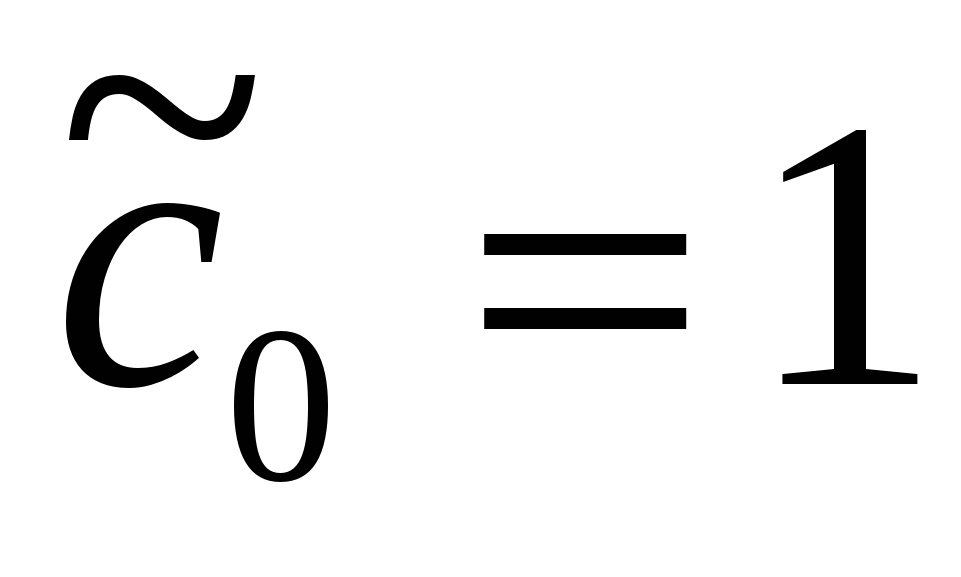 ,
,  ,
, 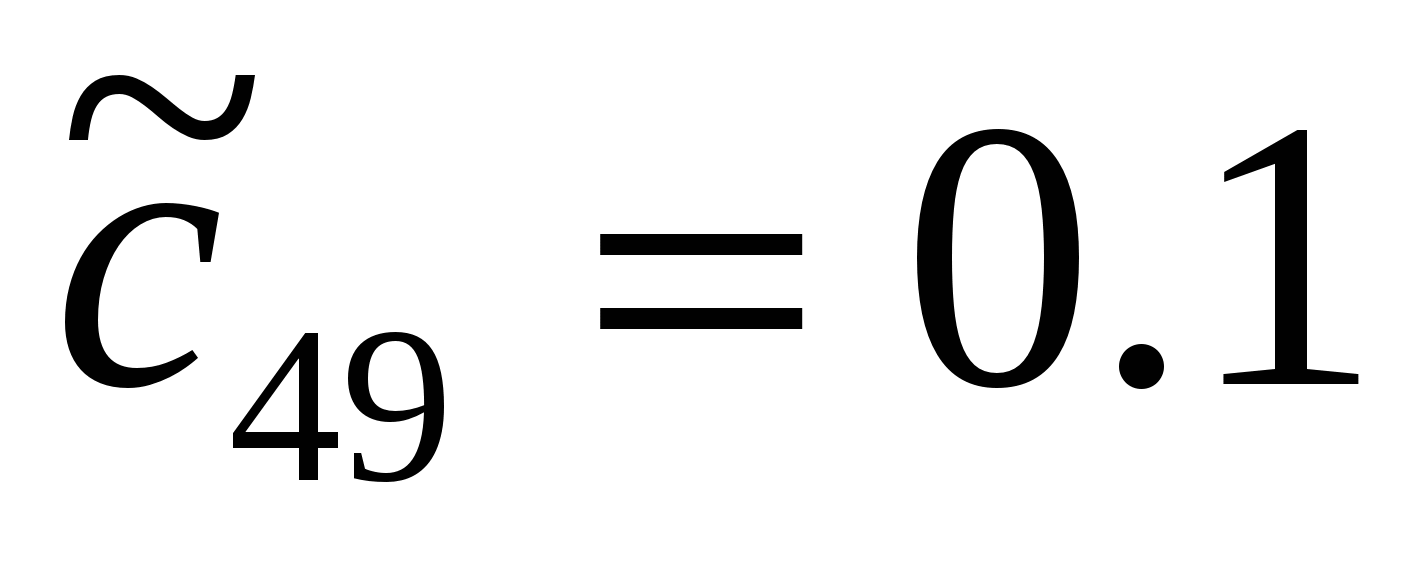 ,
, 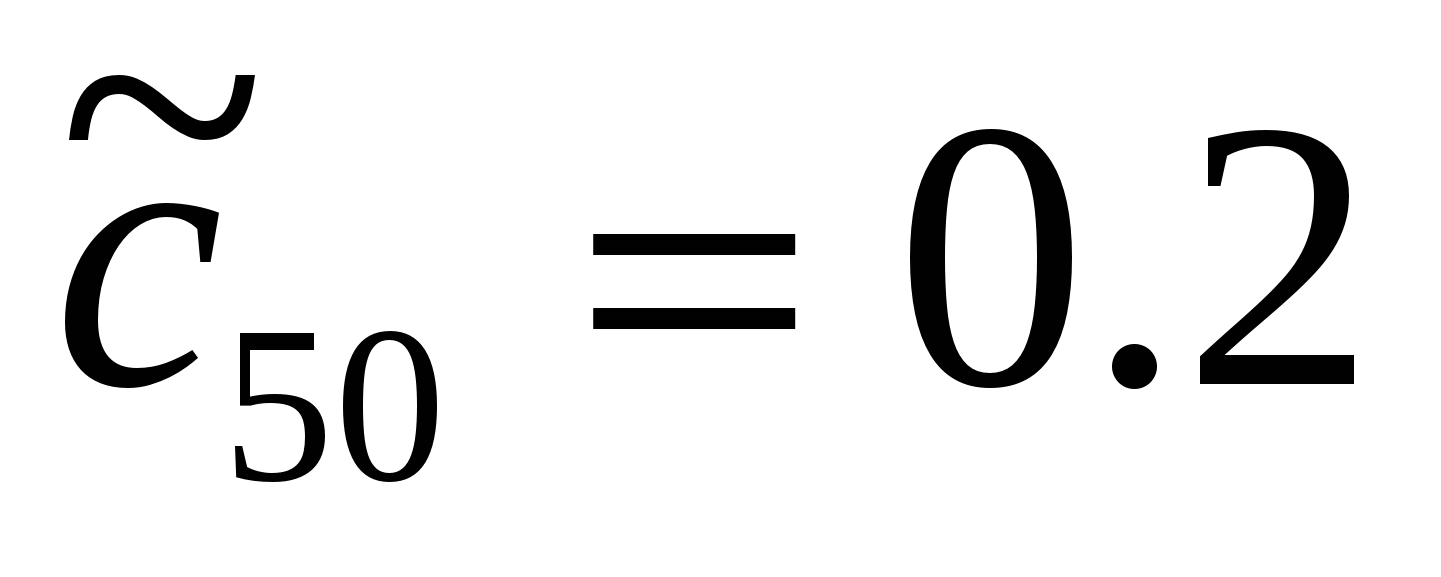 , выбрано
, выбрано 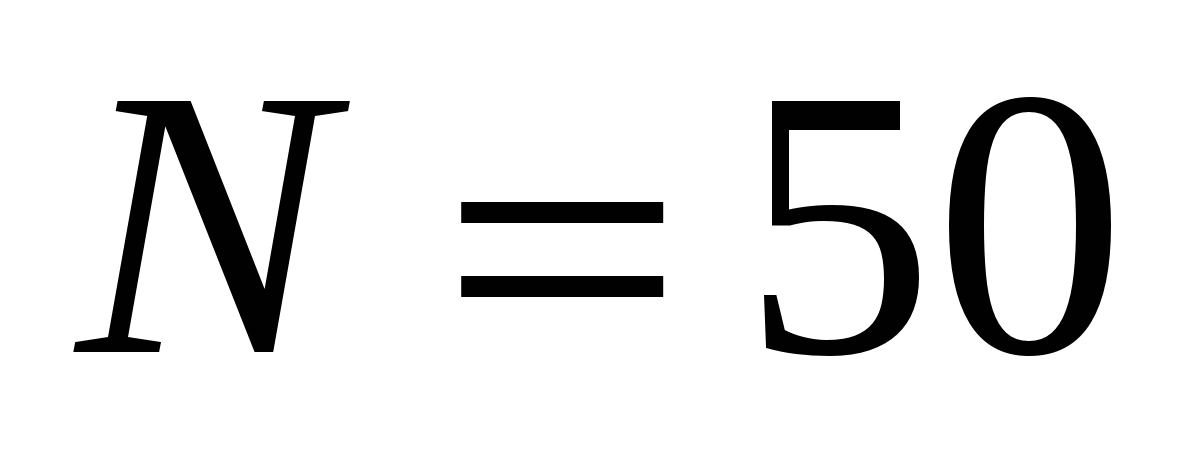 . Это ошибка, т.к. при ДПФ гармоники 50 и 49 накладываются на нулевую и первую соответственно, что даст погрешность 20%. Нужно выбрать
. Это ошибка, т.к. при ДПФ гармоники 50 и 49 накладываются на нулевую и первую соответственно, что даст погрешность 20%. Нужно выбрать 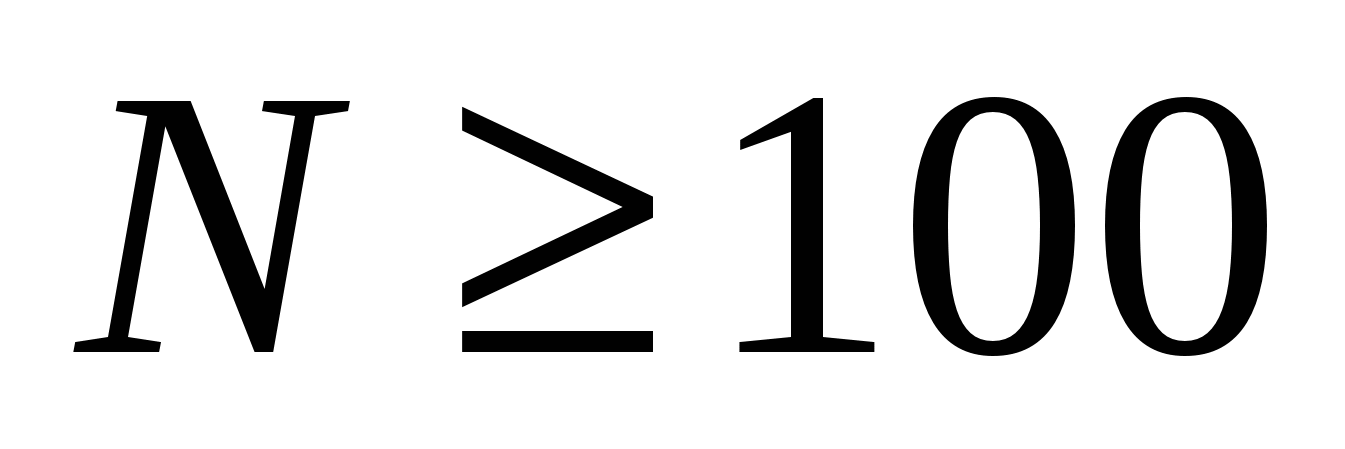 .
.
2.10. Теорема отсчетов.
Другое название теоремы – теорема Котельникова, которое используется в отечественной литературе. Пусть исходный сигнал имеет спектр, ограниченный частотой 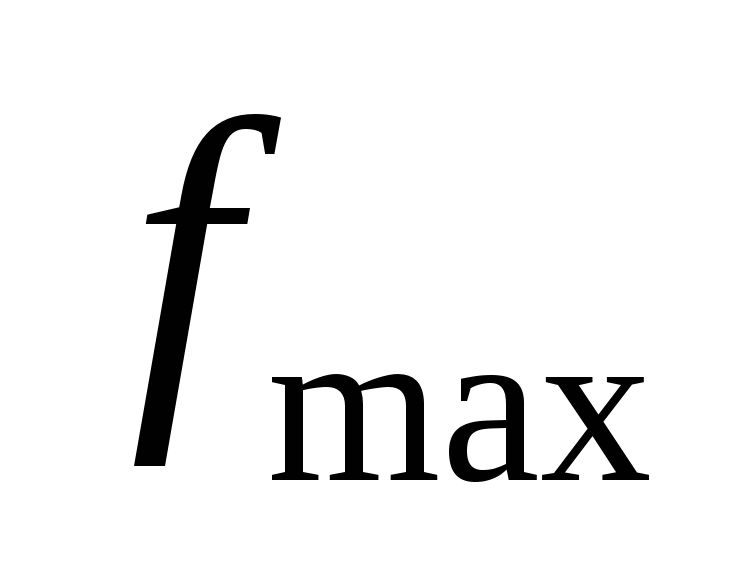 , которая соответствует номеру гармоники
, которая соответствует номеру гармоники 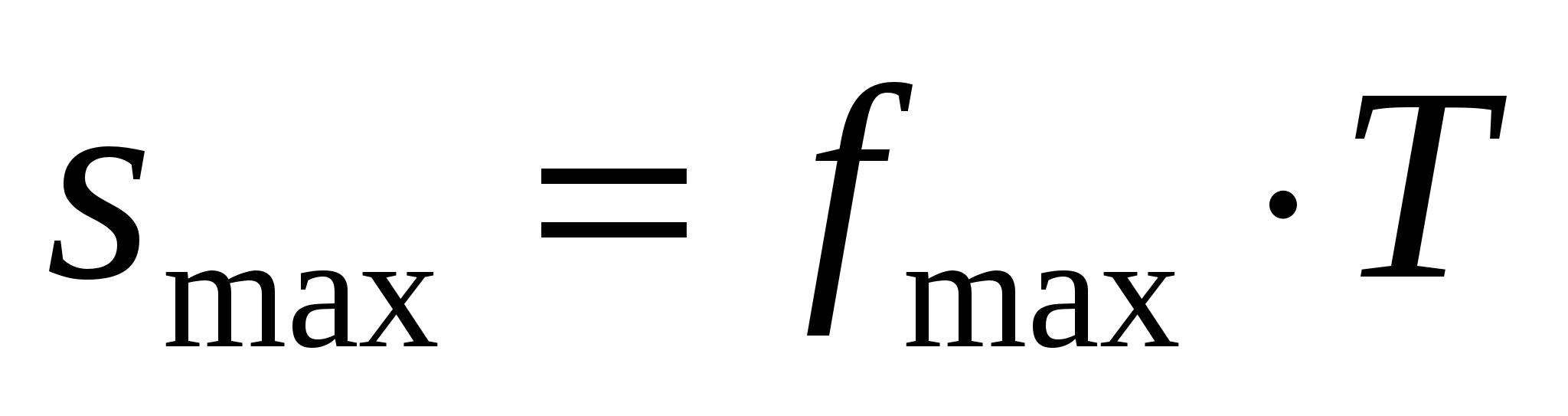 , где
, где 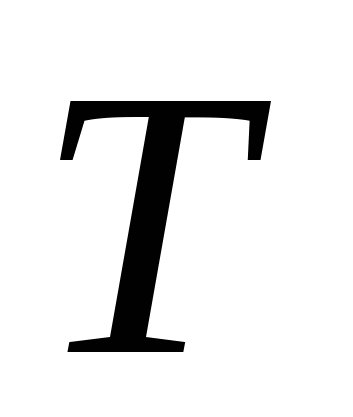 – период сигнала.
– период сигнала.
При дискретизации должно выполняться условие
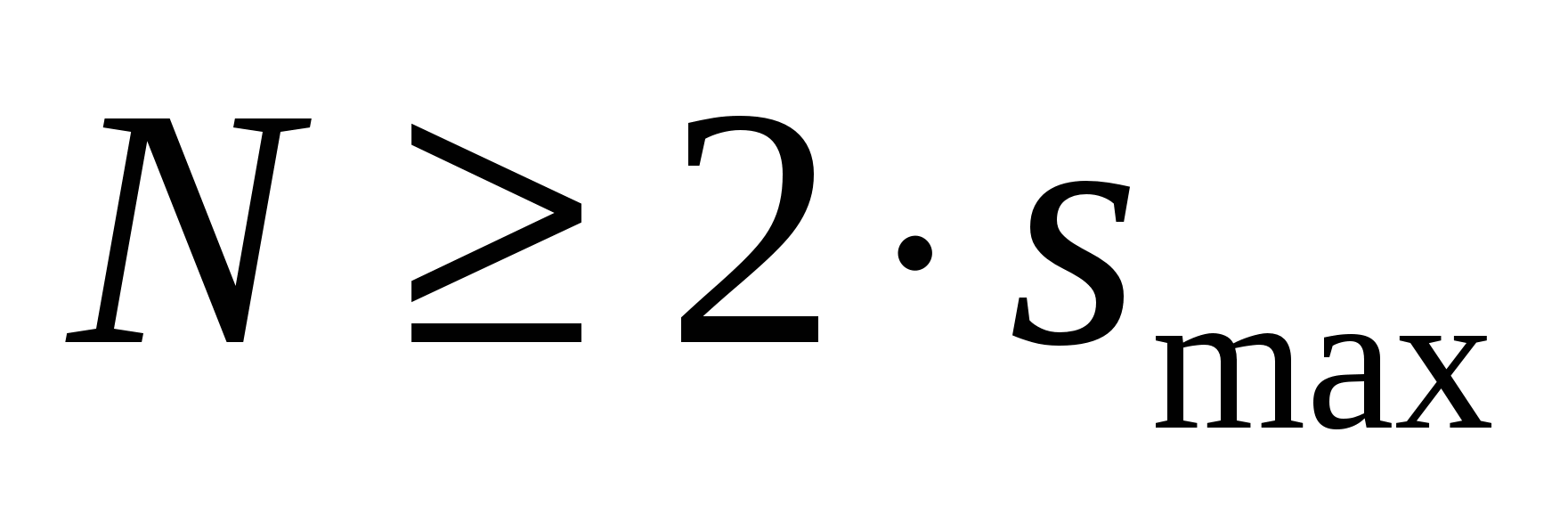 , ,
| (2.27) |
т.е. отсчетов должно быть не меньше удвоенного количества гармоник.
Условие (2.27) можно записать в обычной для ДПФ форме
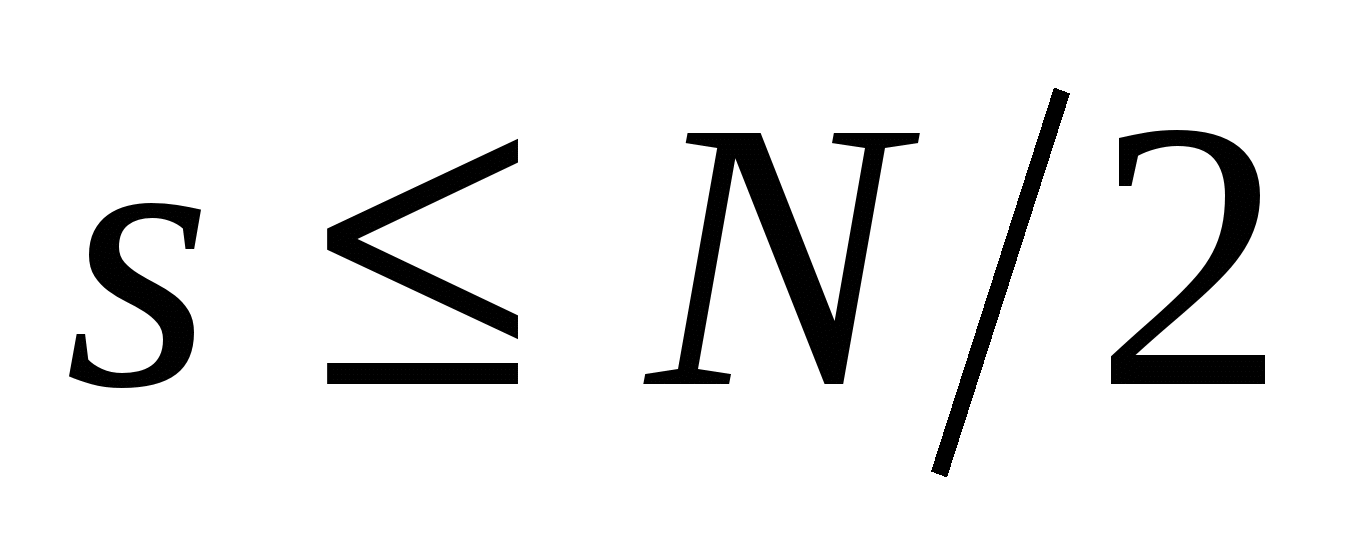 , ,
| (2.28) |
которая использовалась выше.
Формулы (2.27) и (2.28) – это теорема отсчетов в безразмерных переменных. Используя размерные переменные  ,
, 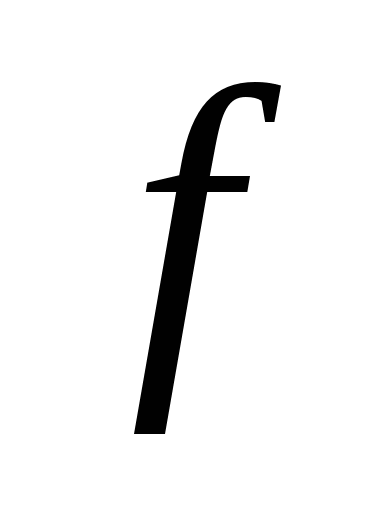 ,
, 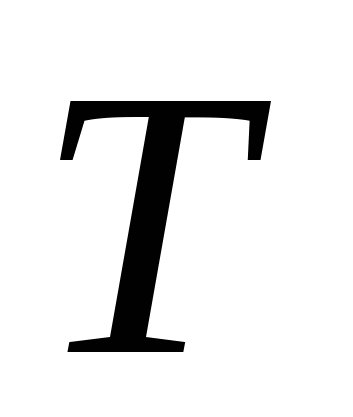 (см. раздел 13.3) и частоту дискретизации
(см. раздел 13.3) и частоту дискретизации 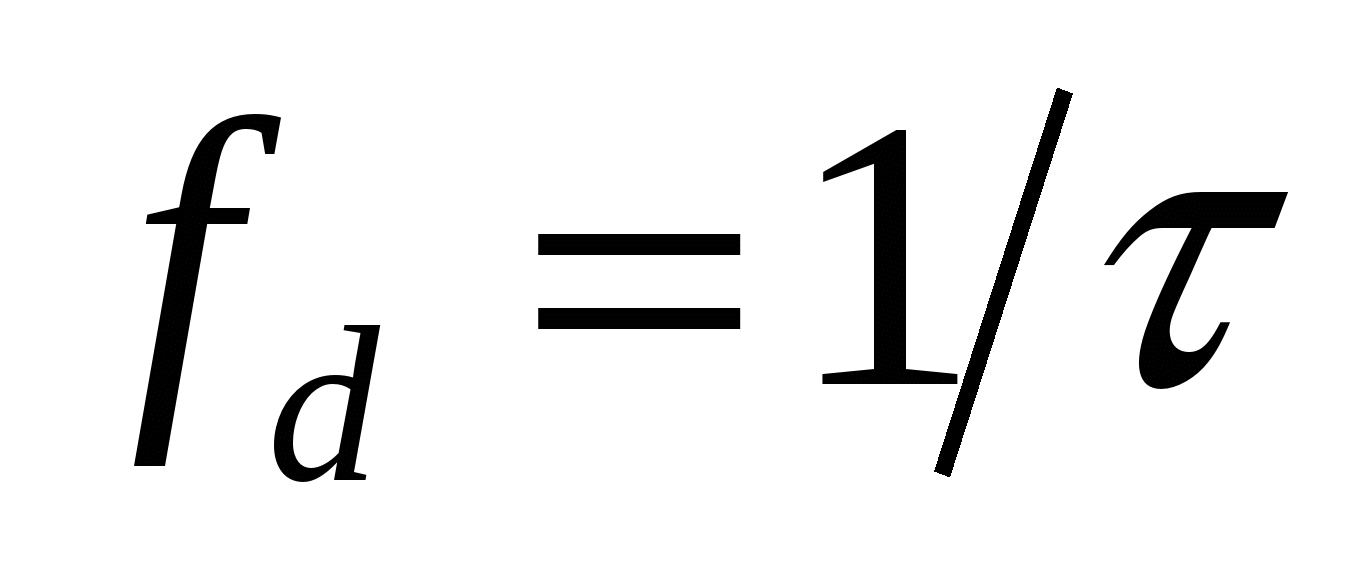 эти формулы можно записать в более известном виде
эти формулы можно записать в более известном виде
 , ,
| (2.29) |
или 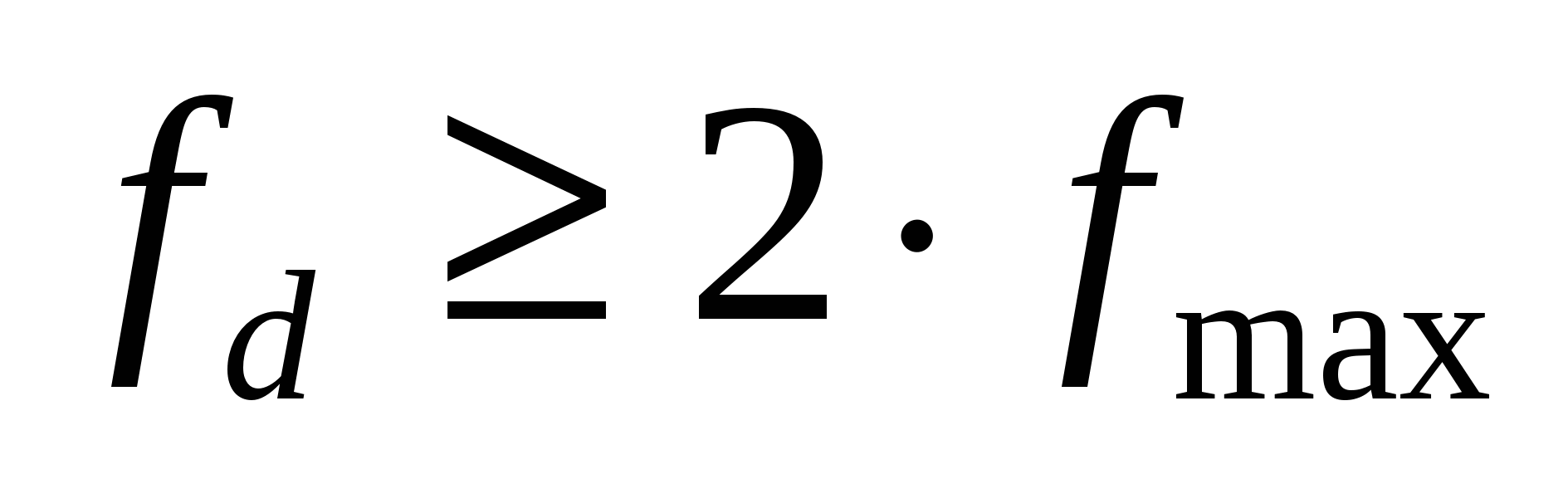 .
.
Дата добавления: 2016-02-20; просмотров: 1244;
