А) Коэффициент корреляции рангов
При регулярной оценке двумя экспертами продукции из группы в п изделий им приписывается значение со знаком «+», когда ранг изделия у первого эксперта выше, чем у второго, и «-», когда нет. Если общую сумму всех разностей оценок обозначить через S, то
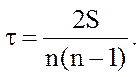 (Д1)
(Д1)
Это выражение является коэффициентом корреляции рангов Кендалла. Отметим, что τ = 1 при совпадении всех рангов у двух экспертов и τ = -1 – при их противоположности. Если учитывать только отрицательные оценки, а их сумму обозначить (-Q), то коэффициент корреляции рангов рассчитывается по формуле
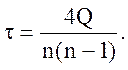 (Д2)
(Д2)
Для определения близости мнений двух экспертов применяется коэффициент корреляции рангов Спирмена:
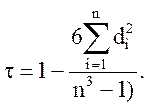 (Д3)
(Д3)
где d – разность рангов.
Кроме того, используя R, можно определить наличие или отсутствие корреляции.
Так, при n > 10
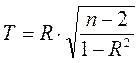 (Д4)
(Д4)
оценка приближенно соответствует t – распределению с (п – 2) – числом степеней свободы.
Пример:
Пусть требуется рассмотреть 10 изделий, которым присвоены порядковые номера, и двум экспертам А и В поручено проранжировать их по убыванию качества (таблица Д1).
| Таблица Д1 – Ранжировки экспертов | ||||||||||
| Изделия | ||||||||||
| Эксперт А | ||||||||||
| Эксперт В | ||||||||||
| Разность рангов 6 | ||||||||||
| Квадрат разностей рангов, d2 |
Переписываем таблицу так, чтобы данные ранжировки эксперта А были упорядочены по возрастанию:
| Эксперт А | ||||||||||
| Эксперт В | ||||||||||
| Инверсии |
Подсчитываем последовательно для результатов эксперта В число данных справа, которое меньше 2, 3, ,11 соответственно, и строим ряд инверсий 1,1, О 0, 1, 1, 1, 1, 0, 0. Сумма числа инверсий Q = 6 и для n =10 коэффициент корреляции рангов Кендалла:
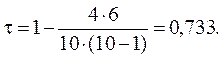 (Д5)
(Д5)
Сумма квадратов разностей 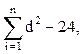 поэтому коэффициент корреляции рангов Спирмена:
поэтому коэффициент корреляции рангов Спирмена:
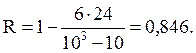 (Д6)
(Д6)
Коэффициент корреляции рангов R равен +1, когда мнения двух экспертов совпадают полностью, а когда они взаимно обратны, коэффициент корреляции равен – 1.
Рассмотрим корреляцию ранжировок, используя tn-2 распределение и полученный R:
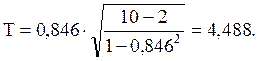 (Д7)
(Д7)
Это значение больше, чем табличной tn(0,01) = 3,335, следовательно, степень близости ранжировок высока.
Дата добавления: 2016-04-06; просмотров: 1167;
