Линейная парная регрессия

Данные о статистической зависимости удобно задавать в виде корреляционной таблицы.

Рассмотрим в качестве примера зависимость между суточной выработкой продукции Y (т) и величиной основных производственных фондов X (млн руб.) для совокупности 50 однотипных предприятий (табл. 1).

В дальнейшем для краткости там, где это очевидно по смыслу, мы часто и выборочные уравнения (линии) регрессии будем называть просто уравнениями (линиями) регрессии.

(В таблице через х_i и у_j обозначены середины соответствующих интервалов, а n_i и n_j — соответственно их частоты).

Изобразим полученную зависимость графически точками координатной плоскости (рис. 1). Такое изображение статистической зависимости называется полем корреляции.

Для каждого значения х_i (i = 1,2,...,l), т.е. для каждой строки корреляционной таблицы вычислим групповые средние

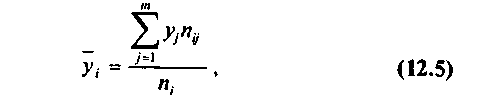(5)

где n_ij — частоты пар (х_i, у_j ) и 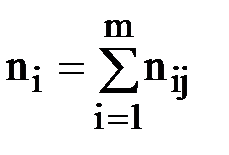, m — число интервалов по переменной Y.

Таблица 1

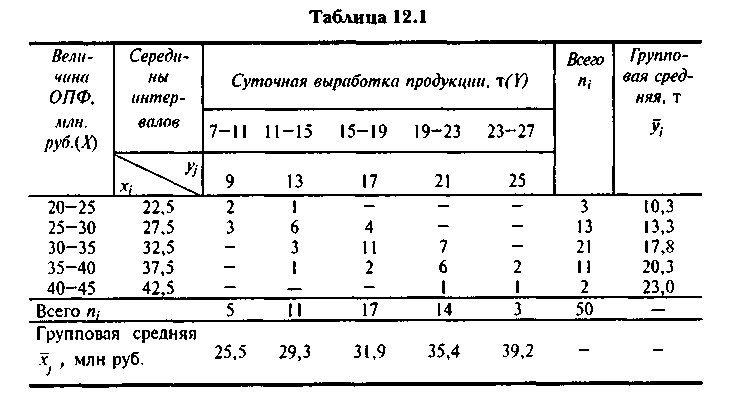
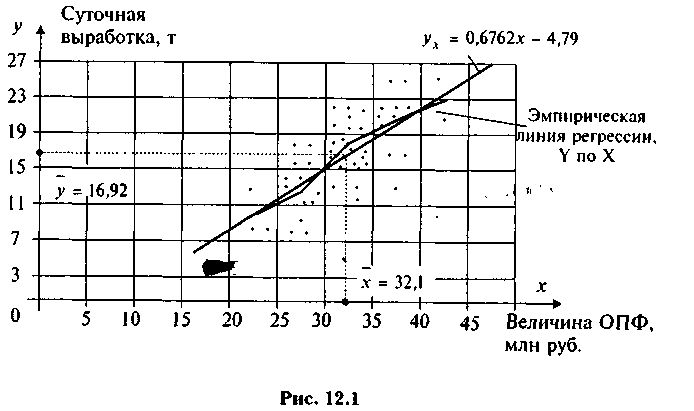
Рис. 1

Вычисленные групповые средние 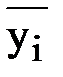поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X (рис. 1).

Аналогично для каждого значения y_j (j = 1,2,...,m) по формуле

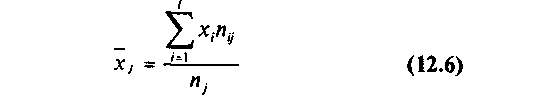(6)

вычислим групповые средние х, (см. нижнюю строку корреляционной таблицы), где 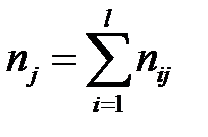, l - число интервалов по переменной X.

По виду ломаной можно предположить наличие линейной корреляционной зависимости Y по X между двумя рассматриваемыми переменными, которая графически выражается тем точнее, чем больше объем выборки (число рассматриваемых предприятий) п:

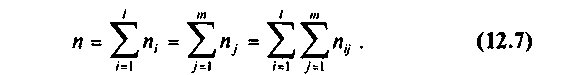(7)

Поэтому уравнение регрессии (3) будем искать в виде:

(8)

Найдем формулы расчета неизвестных параметров уравнения линейной регрессии. С этой целью применим метод наименьших квадратов, согласно которому неизвестные параметры Ь₀ и Ь₁ выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних 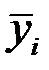вычисленных по формуле (5), от значений 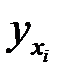, найденных по уравнению регрессии (8), была минимальной:

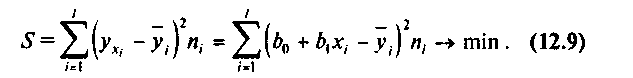(9)

На основании необходимого условия экстремума функции двух переменных S = S(Ь₀, b₁,) приравниваем нулю ее частные производные, т.е.

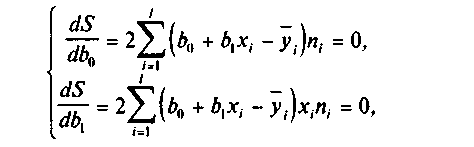
откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:

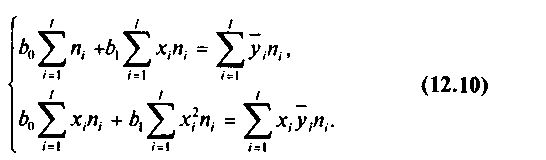(10)

Учитывая (5), преобразуем выражения:

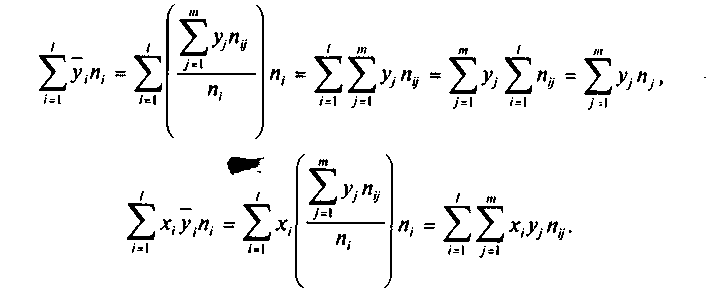
Теперь с учетом (7), разделив обе части уравнений (10) на п, получим систему нормальных уравнений в виде:

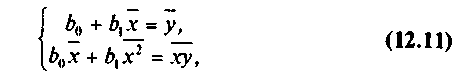(11

где соответствующие средние определяются по формулам:

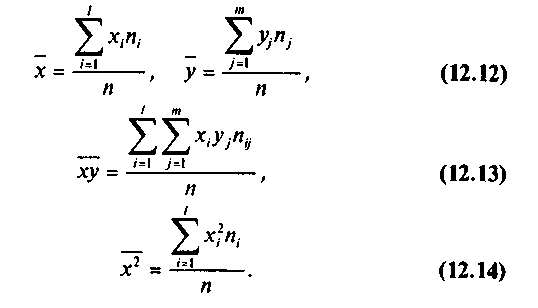
Подставляя значение Ь₀ = 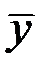- Ь_x из первого уравнения системы (11) в уравнение регрессии (8), получим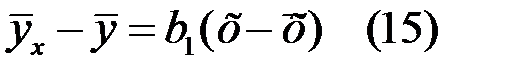

Коэффициент Ь₁ в уравнении регрессии, называемый выборочным коэффициентом регрессии (или просто коэффициентом регрессии) У по X, будем обозначать символом Ь_ух. Теперь уравнение регрессии Y по X запишется так:

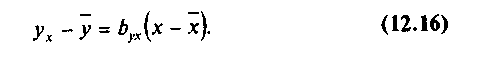
Коэффициент регрессии У по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

Решая систему (12.11), найдем

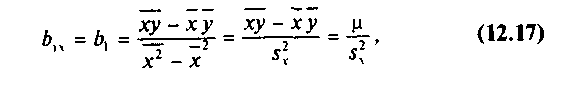
где 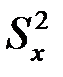— выборочная дисперсия переменной X:

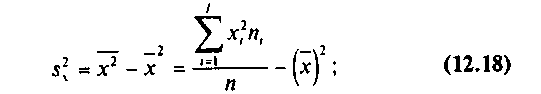
μ — выборочный корреляционный момент или выборочная ковариация:

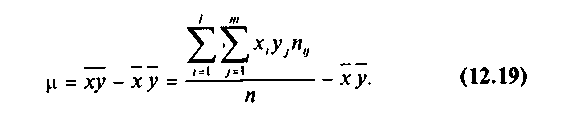
Рассуждая аналогично и полагая уравнение регрессии (4) линейным, можно привести его к виду:

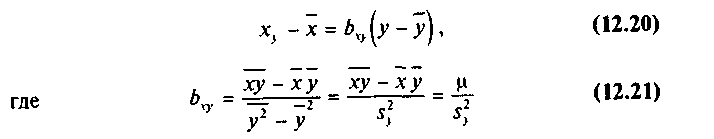
— выборочный коэффициент регрессии (или просто коэффициент регрессии) X по Y, показывающий, на сколько единиц в среднем изменяется переменная X при увеличении переменной У на одну единицу,

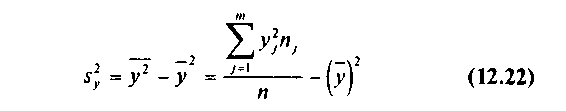
—выборочная дисперсия переменной Y.

Так как числители в формулах (17) и (21) для Ь_yx и Ь_xy совпадают, а знаменатели — положительные величины, то коэффициенты регрессии Ь_yx и Ь_xy , имеют одинаковые знаки, определяемые знаком μ. Из уравнений регрессии (16) и (20) следует, что коэффициенты Ь_yx и 1/Ь_xy определяют угловые коэффициенты (тангенсы углов наклона) к оси oх соответствующих линий регрессии, пересекающихся в точке ( 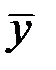, 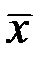) (см. рис. 3).