ИНТЕРПОЛЯЦИЯ И РЕГРЕССИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ В MATHCAD

В практике студента, инженера и учёного часто встречается зада- ча обработки экспериментальных данных. К основным методам обра- ботки можно отнести интерполяцию и регрессию. Известны различные методы интерполяции: по Лагранжу, по Ньютону, каноническими поли- номами, сплайн-интерполяция. Сплайн-интерполяция поддерживается программой MathCAD.

Пусть имеется полученная экспериментальным путём кривая на- магничивания стали 3. Необходимо провести кубическую сплайн- интерполяцию кривой намагничивания и получить в MathCAD интер- поляционную функцию. Введём массив исходных данных в единицах СИ (рис. 2.95).

Рис. 2.95

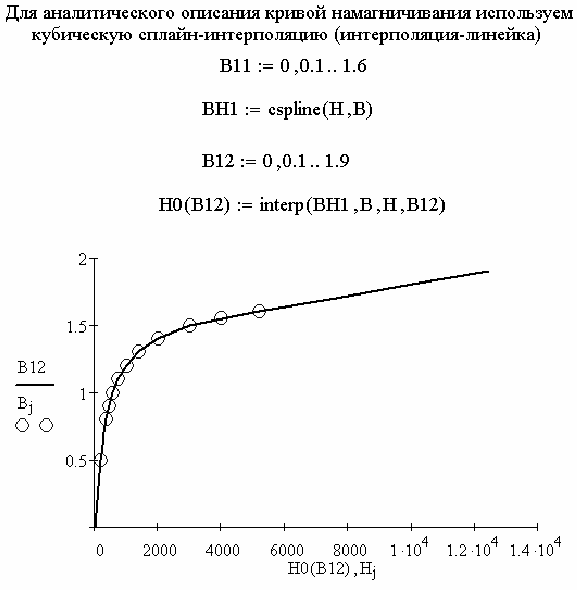Получим в MathCADинтерполяционную функцию (рис. 2.96).

Рис. 2.96

Интерполяционную функцию удобно использовать в магнитных расчётах с применением MathCAD. Достоинством интерполяционной функции является то, что она проходит точно через все узлы интерпо- ляции. При наличии экспериментальных данных с «разбросом» удобно использовать регрессию. В этом случае регрессионная функция прохо- дит не точно через экспериментальные точки. При удачно подобранных

коэффициентах удаётся отсечь «разброс»

ных данных.

в исходных эксперименталь-

цепи

Применим линейную регрессию общего вида к расчёту магнитной электрической машины в MathCAD (рис. 2.97). Видно, что для

представленных исходных данных удачно подобрана аппроксимирую-

щая функция.

.Jimt:eiiuaJI perpecCHH o6I.Qero Bll,!l;a

X- KO.:ltPtPHUHeHT HaCblll.leHrul sy6UOll HaTOpa H pOTOpa aCHHXpQHHOrO

,llBHrareJill

n := length(x) n=9

i:=0..n- 1

'1 •1.l0.l5i

• • •

• • •

...

]+]---I-+---I

----I

• •

---+I-

1.5 2 2.5 3

x;

3a.r aHHe

anpOKoCHMMp)'IOIUCH B&I'IIICJieHHe

KO!l!fl!fll-flllteHfOB

X allpOKCHMI1JlYJOIUCH

2 tPYJiKUilll

¢(x) :=

X

X

exp(x)

X

k := linfit(x,y ,¢)

0.45

-0.096

k = 1.125

0.011

-0.39

<j>l(t):= k-¢(t)

1.2

1>1(r)

--us

Yi

•••

1.1

1.05

1.2 14 1.6 1.8 2 2.2 24 2.6

PHc. 2.97

2.8 3

ГЛАВА 14.