Применение гребенчатой и прямоугольной функций для гармонического анализа в MathCAD

В предыдущем параграфе рассмотрен гармонический анализ на- пряжения на выходе неуправляемого выпрямителя. В случае гармони- ческого анализа выходных напряжений управляемых выпрямителей, ре- гуляторов переменного тока и инверторов для математического описа-

ния исследуемых функций необходимо применять моугольные функции. Зададим в MathCAD период

гребенчатые и пря-

гребенчатой (пило-

образной) функции в единицах СИ для наиболее распространённой час-

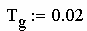тоты 50 Гц (рис. 2.86).

Рис. 2.86

Зададим в MathCAD гребенчатую функцию и построим её график

(рис. 2.87).

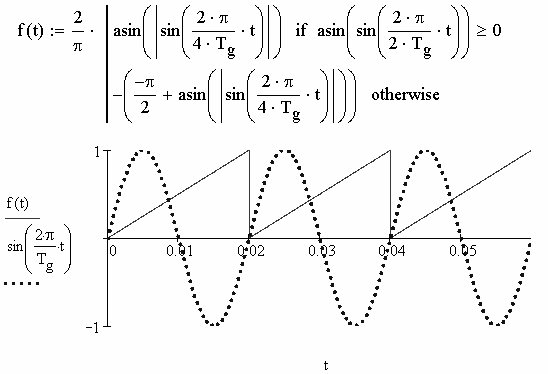Рис. 2.87

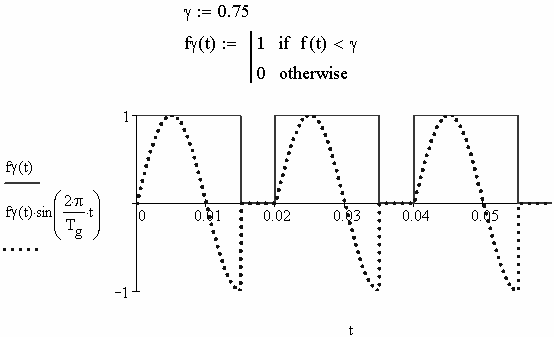Во многих электротехнических устройствах и преобразователях выходное напряжение регулируется скважностью или продолжительно- стью открытого состояния γ. В управляемых выпрямителях и регулято- рах переменного тока выходное напряжение регулируется углом за- держки α (град.). Зададим в MathCAD γ=0.75, объявим прямоугольную функцию скважности f γ(t) и построим её график (рис. 2.88).

Рис. 2.88

Зададим в MathCAD α=90, объявим прямоугольную функцию за-

держки fα(t) и построим её график (рис. 2.89).

3

1 C1

I1

C2

R3 U2

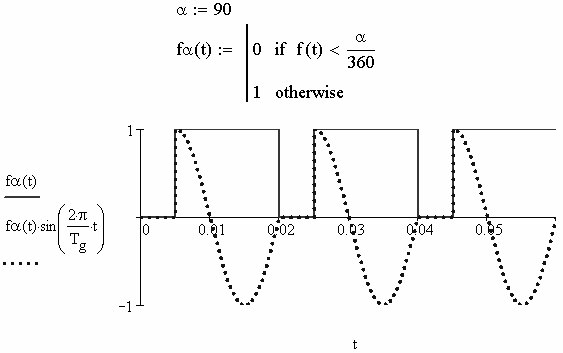Рис. 2.90. Двухзвенный Г-образный LC– фильтр.

Рис. 2.89

ГЛАВА 12.

ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕ-

НИЙ В MATHCAD

Пусть необходимо рассчитать переходные процессы I1(t), I2(t), U1(t), U2(t) при подключении нагруженного двухзвенного Г-образного LC – фильтра к источнику постоянного тока (рис. 2.90).

На первом этапе выводится система из четырёх дифференциальных уравнений (рис. 2.91).

Рис. 2.91

На втором этапе вводим параметры фильтра и функции правых

частей дифференциальных уравнений (рис. 2.92).

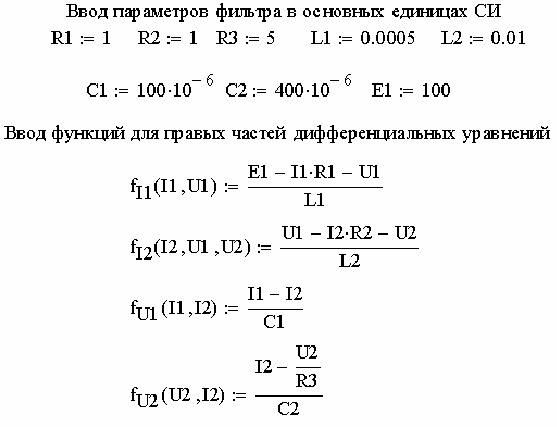Рис. 2.92

Шаг

расчёта рекомендуется брать пропорциональным среднегео-

метрической величине от всех постоянных времени фильтра (рис. 2.93).

Рис. 2.93

Решение методом Эйлера системы дифференциальных уравнений,

описывающих состояние фильтра, с нулевыми начальными условиями

показано на рис. 2.94. Здесь же показаны полученные графики переход-

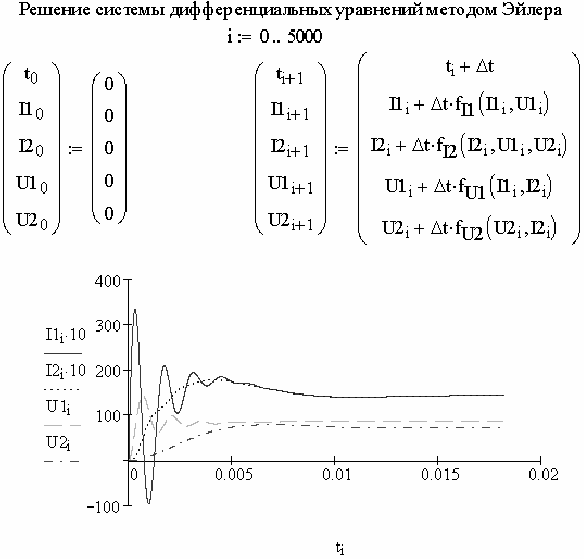ных процессов.

Рис. 2.94

Процедура расчёта переходных процессов в MathCAD простей-

шим методом (Эйлера) сводится к следующим этапам:

– вывод системы дифференциальных уравнений, описывающих

устройство;

– ввод параметров устройства;

– ввод функций правых частей дифференциальных уравнений;

– расчёт или задание шага интегрирования;

– ввод начальных условий;

– запись расчётной процедуры;

– построение графиков.

ГЛАВА 13.