ПОСТРОЕНИЕ И АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК В
MATHCAD
Рассмотрим задачу получения и анализа частотных характеристик однозвенного нагруженного Г-образного LC-фильтра низких частот (рис. 2.52) с применением MathCAD.
В главе 8 выведено выражение (2.15) для операторной передаточ- ной функции ФНЧ. Пусть ω – частота входного сигнала (напряжения) ФНЧ, а j – мнимая единица. Заменим в (2.15) оператор Лапласа s на
комплексную переменную j·ω
W( j⋅ω) =
(L⋅ j⋅ω+ R)⋅⎛C⋅ j⋅ω+
.
1 ⎞ +1
(2.19)
⎜ ⎟
⎝ RНАГР ⎠
Преобразуем знаменатель выражения (2.19), выделив действи-
тельную и мнимую части
W( j⋅ω) =
1 − L⋅C⋅ω2 +
1 .
R + j⋅ω⋅⎛ R⋅C+ L ⎞
(2.20)
⎜ ⎟
RНАГР
⎝ RНАГР ⎠
Напомним, что в математике известна процедура избавления от мнимой единицы в знаменателе выражения
1 ⋅ a −
j ⋅b = a −
j ⋅b =
a − j ⋅ b
. (2.21)
a +
Приняв
j ⋅ b a −
j ⋅ b a2 + b2
a2 + b2
a2 + b2
a = 1 − L ⋅ C ⋅ ω 2 +
R RНАГР
(2.22)
и
b = ω ⋅⎛ R ⋅C +
L ⎞ (2.23)
,
⎜ ⎟
⎝ RНАГР ⎠
и, учитывая (2.20) можно записать выражение для комплексной частот-
ной характеристики ФНЧ
1 − L ⋅ C ⋅ ω 2 +
R
RНАГР
(2.24)
W( j⋅ω) =
2 2 −
⎛
1 − L⋅C⋅ω2 +
R ⎞ + ω2 ⋅⎛ R⋅C+ L ⎞
⎜ ⎟ ⎜ ⎟
⎝ RНАГР ⎠ ⎝
RНАГР ⎠
ω⋅⎛ R⋅C+ L ⎞
⎜ ⎟
| 2 2 |
⎛
1 − L⋅C⋅ω2 +
R ⎞ + ω2 ⋅⎛ R⋅C+ L ⎞
⎜ ⎟ ⎜ ⎟
где
⎝
= P (ω )+
RНАГР ⎠ ⎝
j ⋅ Q (ω ) = A(ω )⋅ e j⋅ϕ(ω),
RНАГР ⎠
P(ω) =
1 − L ⋅ C ⋅ ω 2 +
R
RНАГР
(2.25)
–
2 2
⎛
1− L⋅C⋅ω2 +
R ⎞ + ω2 ⋅⎛ R⋅C+ L ⎞
⎜ ⎟ ⎜ ⎟
⎝ RНАГР ⎠ ⎝
RНАГР ⎠
– вещественно-частотная характеристика (ВЧХ) ФНЧ,
ω⋅⎛ R⋅C+ L ⎞
(2.26)
⎜ ⎟
⎝ RНАГР⎠
Q (ω )=−
⎛
1 − L⋅C⋅ω2 +
2 2 –
R ⎞ +ω2 ⋅⎛ R⋅C+ L ⎞
⎜ ⎟ ⎜ ⎟
⎝ RНАГР ⎠ ⎝
RНАГР ⎠
– мнимо-частотная характеристика (МЧХ) ФНЧ,
A(ω) = W( j⋅ω) =
P(ω)2 + Q(ω)2 –
(2.27 )
– амплитудно-частотная характеристика (АЧХ) ФНЧ,
ϕ(ω) = argW( j⋅ω) = arctgQ(ω) –
P(ω)
– фазо-частотная характеристика (ФЧХ) ФНЧ.
(2.28)
Вектор (2.24) на комплексной плоскости частотных характеристик
можно описать либо с помощью пары
P (ω )
и Q (ω ), либо с помощью
A(ω)
и ϕ(ω) . Наибольший интерес с практической точки зрения пред-
ставляют
A(ω)
и ϕ(ω) .
Введём исходные данные в MathCAD(рис. 2.64).
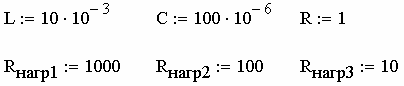 Рис. 2.64
Рис. 2.64
Введём функции (2.25-2.28) в MathCAD(рис. 2.65).
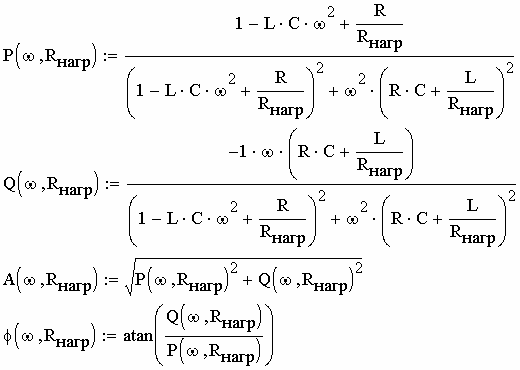 Рис. 2.65
Рис. 2.65
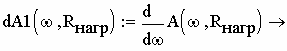 Для нахождения резонансной частоты ФНЧ необходимо АЧХ продифференцировать по частоте ω и ввести результат соответствую- щую функцию (рис. 2.66).
Для нахождения резонансной частоты ФНЧ необходимо АЧХ продифференцировать по частоте ω и ввести результат соответствую- щую функцию (рис. 2.66).
Рис. 2.66
Приравняем производную к нулю и решим нелинейное уравнение с помощью процедуры solve (рис. 2.67).
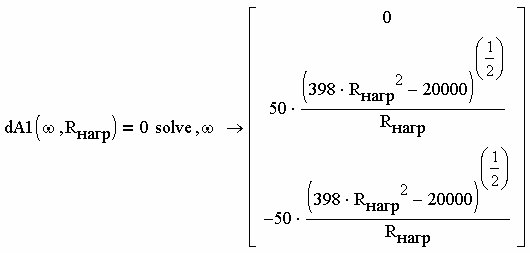 Рис. 2.67
Рис. 2.67
Отбросим первый и третий полученные корни, а второй корень представим в виде функции, затем определим резонансные частоты при трёх значениях сопротивления нагрузки (рис. 2.68).
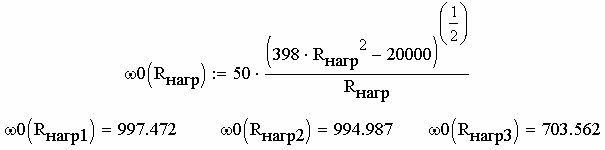 Рис. 2.68
Рис. 2.68
Амплитудно-частотные характеристики ФНЧ при разных сопро-
тивлениях нагрузки представлены на рис. 2.69.
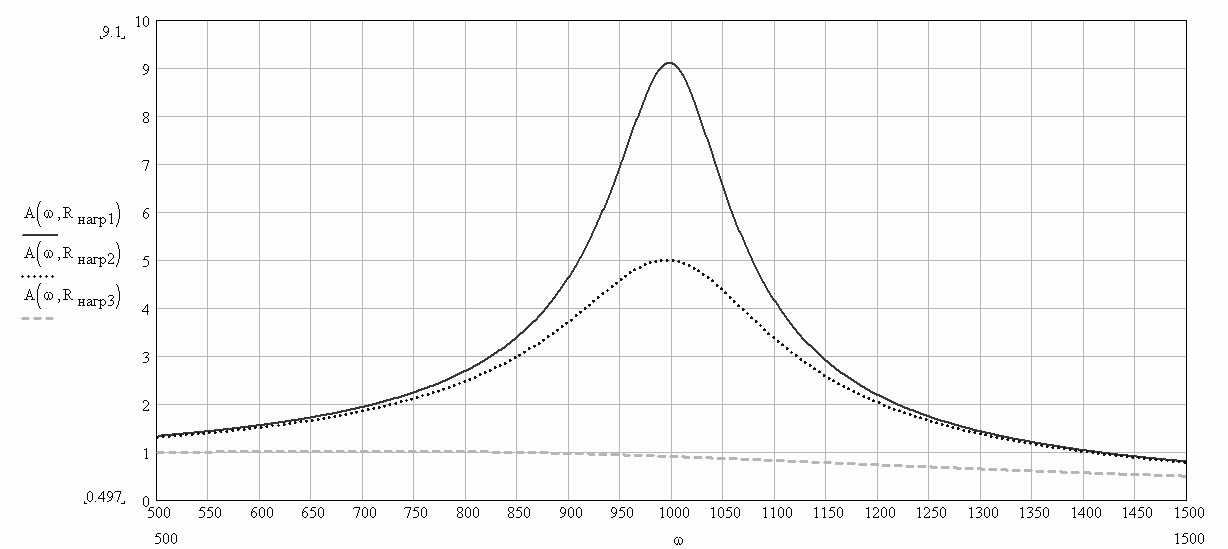

Рис. 2.69
Резонансная частота ФНЧ нелинейно зависит от сопротивления нагрузки (рис. 2.70).
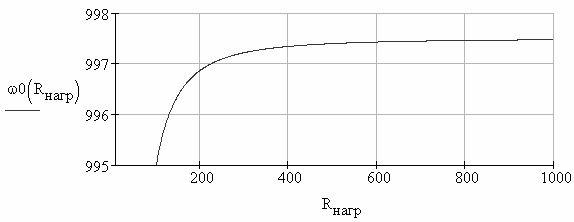 Рис. 2.70
Рис. 2.70
Фазо-частотные характеристики ФНЧ при разных сопротивлениях нагрузки представлены на рис. 2.71.
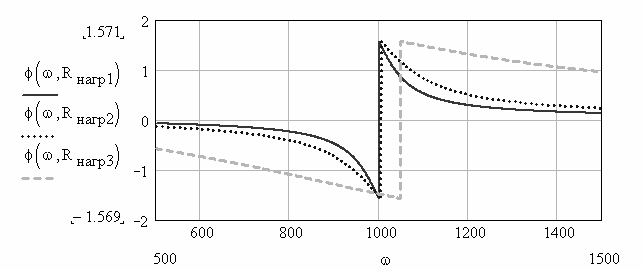 Рис. 2.71
Рис. 2.71
Если
повышать частоту
входного сигнала ФНЧ начиная от резо-
нансной, то амплитуда выходного напряжения при некоторой частоте
снизится в
2 раз по сравнению с амплитудой при частоте, стремящей-
ся к нулю. Такая частота определяет полосу пропускания ФНЧ. Опреде-
лим
полосу пропускания ФНЧ при ненагруженном режиме, решив не-
линейное уравнение с помощью процедур solve. Результат представим в
формате float (с плавающей точкой), взяв первые 6 значащих цифр ре-
зультата (рис. 2.72).
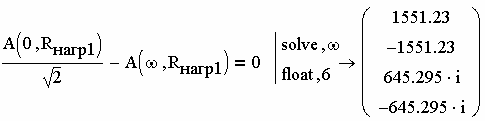 Рис. 2.72
Рис. 2.72
Истинным решением будет первый корень, так как он является действительным положительным числом.
Найдём полосы пропускания ФНЧ при втором и третьем сопро-
тивлениях нагрузки (рис. 2.73).
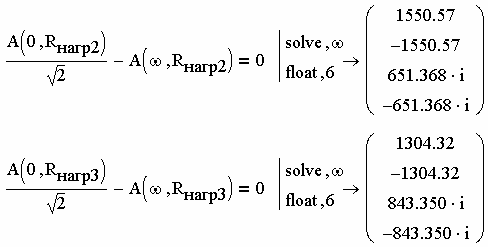 Рис. 2.73
Рис. 2.73
Аналогично истинным решением будет в обоих случаях первый корень, так как он является действительным положительным числом.
Численные результаты расчётов в ной главе внесём в табл. 2.2.
MathCAD, полученные в дан-
Таблица 2.2
| Показатель | Сопротивление нагрузки | ||
| RНАГР1 | RНАГР2 | RНАГР3 | |
| Резонансная частота, ω0 , Гц | 997.472 | 994.987 | 703.562 |
| Полоса про- пускания, ωПП , Гц | 1551.23 | 1550.57 | 1304.32 |
Как видно из табл. 2.2 резонансная частота и полоса пропускания ФНЧ при увеличении загруженности фильтра смещаются в сторону низких частот.
ГЛАВА 11.
Дата добавления: 2016-04-02; просмотров: 975;
