Определение параметров рабочей точки по внешней характери- стике асинхронного двигателя и нагрузочной характеристике тур- бомеханизма встроенными средствами MathCAD

На основе решения задачи, приведённого в предыдущем парагра- фе, покажем определение параметров рабочей точки встроенными сред- ствами MathCAD.

Введём разностную функцию (рис. 2.45),

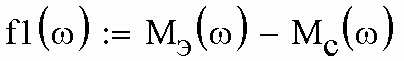Рис. 2.45

график которой представлен на рис. 2.46.

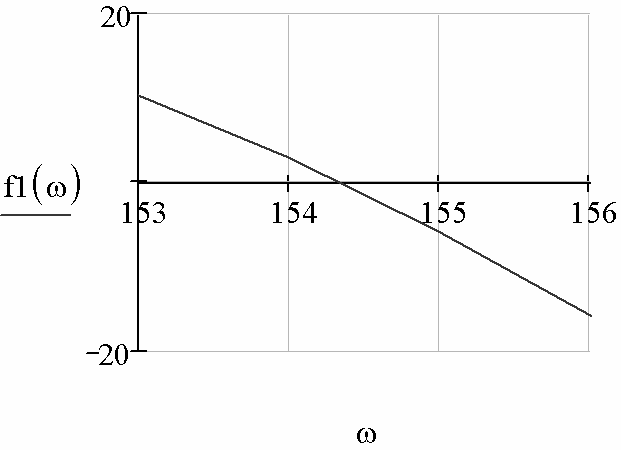Рис. 2.46

Разностная функция пересекает ось абсцисс при такой величине ω, которая соответствует искомой. Задача сводится к решению нели- нейного уравнения в окрестности точки ω=154 рад/с, определённой в предыдущем параграфе.

Покажем три способа решения.

Первый способ представлен на рис. 2.47. Вводим начальное при-

ближение ω1=154 рад/с по данным графического решения. Вызываем функцию root. В качестве переменных этой функции указываем разно-

стную функцию f1(ω1) и переменную ω1. Функция возвращает ответ ω=154.351 рад/с.

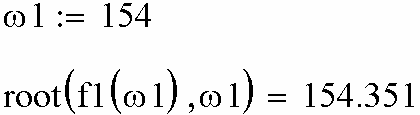Рис. 2.47

Второй способ представлен на

рис. 2.48. Вводим начальное при-

ближение ω2=154 рад/с по данным графического решения. Вводим ключевое слово Given. Вводим нелинейное уравнение. Переменной w1 присваиваем результат вычисления функции find. В качестве перемен- ной этой функции указываем переменную ω2. Полученный ответ w1=154.351 рад/с совпадает с ответом, полученным с помощью первого способа.

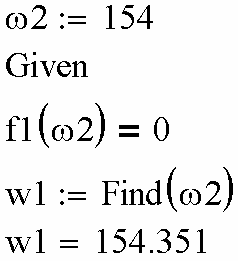Рис. 2.48

Третий способ представлен на рис. 2.49. Для решения задачи вы- бран метод дихотомии – метод половинного деления отрезка, на кото- ром ведётся поиск. На первом этапе задаются концы отрезка: ωmin=154 рад/с – начало, ωmax=155 рад/с – конец, что соответствует данным, полу- ченным при графическом решении (рис. 2.44). Задаём функцию fω(∆),

где ∆ – точность ответа, с применением элементов

программирования,

встроенных в MathCAD, доступных для пользователя (см. панель 4, рис.

2.1). В теле программы используются кнопки Add Line (добавить строку программы), ← (локальное определение), while (цикл с условием про-

должения),

логическое «больше

или равно», if(условный оператор),

otherwise (оператор «иначе»), функция знака sign(x) (равна 1, если число x положительное, -1 – если x отрицательное и 0, если x=0). Нетрудно проследить работу представленной программы. Чем выше требуется точность ответа, тем больше итераций потребуется для решения задачи. При ∆=0.01 в ответе получим ω=154.351 рад/с.

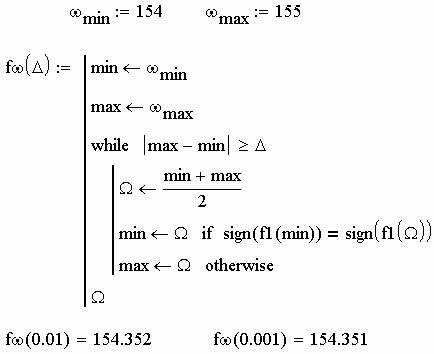Рис. 2.49

Подставив ω=154.351 рад/с, найденное одним из вышеописанных способов, в выражение для механической характеристики АД (рис.

2.41), получим вторую искомую координату Mэ=27.355 Нм (рис. 2.50).

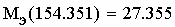Рис. 2.50

В данной главе на

примере решения типовой задачи показана

возможность автоматизации расчётов с применением MathCAD.

ГЛАВА 8.