ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ПЕРЕХОДНЫЕ ФУНКЦИИ
Рассмотрим задачу получения и анализа импульсных переходных характеристик однозвенного нагруженного Г-образного LC-фильтра низких частот (ФНЧ).
Пусть ФНЧ коммутируют на источник постоянного тока Uвх при трёх значениях сопротивления нагрузки: 10·R (нагруженный режим),
100·R (нормальный режим), 1000·R (ненагруженный режим) (рис 2.53). Необходимо с применением обратного преобразования Лапласа полу- чить импульсные переходные характеристики для всех значений сопро- тивления нагрузки, определить время переходного процесса и перерегу- лирование. Результаты внести в таблицу.
L R
UВХ
C RНАГР
UВЫХ
Рис. 2.53
Вводим в MathCADисходные данные (рис. 2.54).
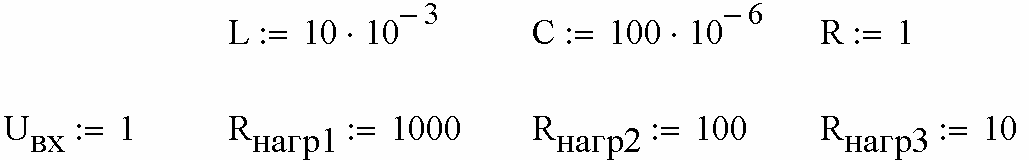 Рис. 2.54
Рис. 2.54
С учётом (2.15) запишем выражение для выходного напряжения
ФНЧ в операторной форме
UВЫХ
(s ) = U ВХ
s
⋅ 1
(L ⋅ s + R)⋅⎛C ⋅ s +
,
1 ⎞ +1
(2.16)
⎜ ⎟
⎝ RНАГР ⎠
где
UВХ
s
– операторная форма входного напряжения, прикладываемого
ступенчато при коммутации ключа (рис. 2.53).
Упростим в MathCADвыражение (2.16) с применением оператора
упрощения выражений simplify для
RНАГР1 =1000 ⋅ R
(рис. 2.55).
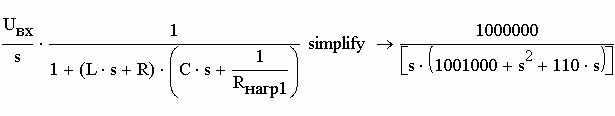 Рис. 2.55
Рис. 2.55
К выражению, полученному в результате упрощения, применим обратное преобразование Лапласа с учётом нулевых начальных условий (до коммутации токи и напряжения ФНЧ равны нулю) (рис. 2.56).
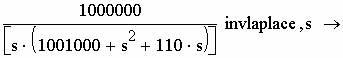 Рис. 2.56
Рис. 2.56
Получаем переходную функцию ФНЧ в ненагруженном режиме
| ( |
1001 1001
39919 ⋅ t )−
(2.17 )
− 1000
⋅ exp (−55 ⋅ t )⋅
39919 ⋅ sin (5 ⋅
39919 ⋅ t )
и вводим её в MathCAD. Напомним, что операция присвоения в Math-
CAD производится как :=.
Аналогично получим в MathCADпереходные функции ФНЧ:
h2 (t )
h3(t )
– в нормальном ( RНАГР 2 = 100 ⋅ R ) и
– в нагруженном режимах (рис. 2.57).
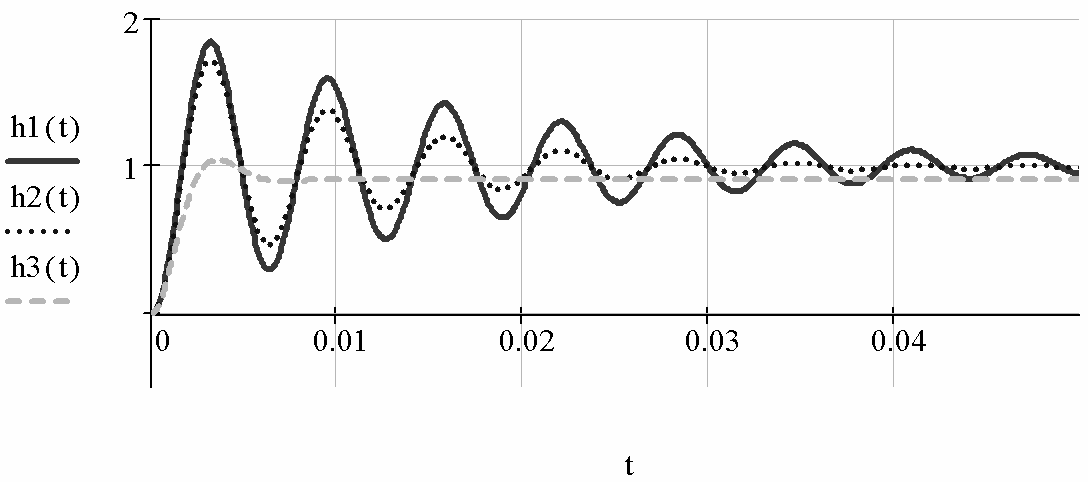 Рис. 2.57
Рис. 2.57
Как видно из рис. 2.57 переходные процессы имеют колебатель-
ный характер с перерегулированием и стремятся при t→∞ к установив-
шимся значениям
h1(∞) ≈ h1(100) ,
h2 (∞) ≈ h2 (100) ,
h3(∞) ≈ h3(100) .
Переходный процесс
h1(t)
заканчивается, если
h1(t) ≤1.05 ⋅ h1(∞) и
h1(t) ≥ 0.95 ⋅ h1(∞) , или, по-другому,
h1(t) последний раз входит в зону
допустимых отклонений
h1(∞) ± 0.05 ⋅ h1(∞) . Время переходного про-
цесса в MathCADможно определить графически и численно. Переход-
ный процесс
h1(t)
последний раз пересекает нижнюю границу зоны до-
пустимых отклонений при 0.051 с (рис. 2.58), верхнюю – при 0.054 с
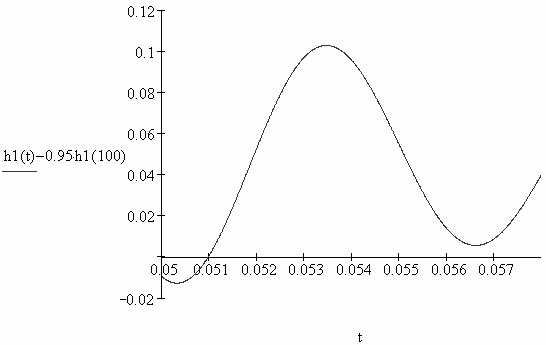 (рис. 2.59), следовательно, tПП1 = 0.054 с .
(рис. 2.59), следовательно, tПП1 = 0.054 с .
Рис. 2.58
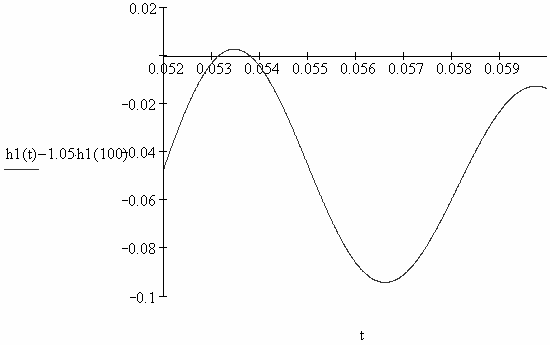 Рис. 2.59
Рис. 2.59
Аналогично в MathCADопределяем:
– для
h2 (t ) время переходного процесса tПП2 = 0.029 с и
– для
h3(t )
время переходного процесса tПП3 = 0.005 с .
Перерегулирование для переходной характеристики
делим как
h1(t )
опре-
h1(tm1)− h1(∞)
h1(tm1)− h1(100)
(2.18)
∆h1 = ⋅100% ≈ ⋅100% ,
h1(∞)
h1(100)
где tm1 – время достижения функцией
h1(t)
первого максимума.
Для определения tm1найдём в MathCAD производную
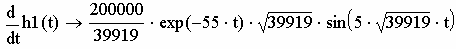 (рис. 2.60).
(рис. 2.60).
h1(t )
по t
Объявим функцию
dh1(t)
Рис. 2.60
(рис. 2.61).
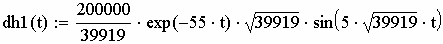 Рис. 2.61
Рис. 2.61
Графически определим время
tm1в первом приближении (рис. 2.62).
tt1 = 0.00314 c , что соответствует
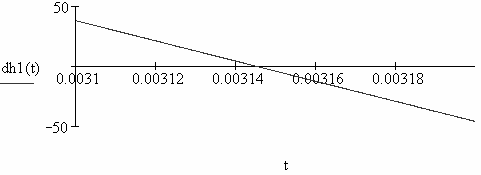 Рис. 2.62
Рис. 2.62
Используя процедуру findи учитывая (2.18) определяем, что пе-
ререгулирование переходной функции
(рис. 2.63).
h1(t )
составит
∆h1 = 84.117%
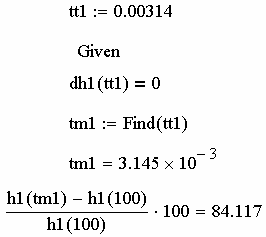 Рис. 2.63
Рис. 2.63
Аналогично в MathCADопределяем:
– для
h2 (t) перерегулирование
∆h2 = 73.04% и
– для
h3(t)
перерегулирование
∆h3 = 13.04% .
Полученные в данной главе результаты внесём в табл. 2.1.
Таблица 2.1
| Показатель | Сопротивление нагрузки | ||
| RНАГР1 = 1000 ⋅ R | RНАГР 2 = 100 ⋅ R | RНАГР3 = 10 ⋅ R | |
| Время переход- ного процесса | tПП1 = 0.054 с | tПП2 = 0.029 с | tПП3 = 0.005 с |
| Перерегулирова- ние | ∆h1 = 84.117% | ∆h2 = 73.04% | ∆h3 = 13.04% |
Как видно из табл. 2.1, с увеличением загруженности ФНЧ
уменьшается время переходного процесса и перерегулирование.
ГЛАВА 10.
Дата добавления: 2016-04-02; просмотров: 988;
