Ex post прогнозы для второй группы данных
ИСПОЛЬЗОВАНИЕ АЛГОРИТМА ЕX POST ДЛЯ АНАЛИЗА ТРЕНДОВИХ МОДЕЛЕЙ
- Алгоритм ex post прогнозирования.
Тестирование трендовых моделей с помощью ex post прогнозирования
Одной из характеристик, отражающих точность, с которой модель описывает процесс, является коэффициент детерминации R2.
При этом естественно нет никакой гарантии, что даже при значении R2, близком к единице, такая модель будет давать хорошие прогнозы. Могут произойти какие-нибудь структурные изменения в самой организации или во внешних экономических или других условиях (например, изменения в налогообложении). Поскольку подобные изменения происходят постоянно, необходимо узнать, как выбранная модель реагировала бы на них в прошлом. Это и есть идея ex post прогнозирования.
С этой целью исходные данные разбиваются на две группы, так чтобы во второй группе находились более поздние данные, составляющие обычно примерно 15% всей информации. Эти данные будут затем использоваться для тестирования. При небольшом объеме исходных данных во второй группе можно рассматривать до 30% исходной информации.
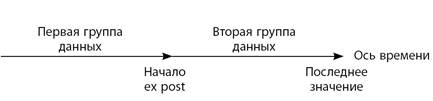
Рис.1. Ex post прогнозирование
Пример: Известны объемы продаж компании за 17 кварталов.
Таблица 1
Исходные данные
| Квартал t | Объем продаж, тыс.грн. |
Разобьем данные в табл. 1. следующим образом. К первой группе отнесем данные за первые 13 кварталов А ко второй группе — данные за оставшиеся четыре квартала (т. е. с 14-го по 17-й квартал).
Следующую процедуру можно охарактеризовать как имитацию процесса прогнозирования: мысленно перенесемся на год назад относительно времени самого последнего значения и начнем прогнозировать так, как если бы сейчас был конец 13-го квартала . Прогнозы, полученные таким образом, называются ex post прогнозами.
При этом каждый раз сравниваются полученные значения с имеющейся информацией.В этом как раз и состоит главное преимущество ex post прогнозирования . При обычном прогнозировании такой возможности нет.
Алгоритм Ex post прогнозирования:
1. Находим трендовую модель для первых 13 кварталов.
2. Из уравнения определяем прогноз на 14-й квартал.
3. Сравниваем полученный прогноз с имеющейся информацией за 14-й квартал. Находим ошибку.
4. Повторяем пункты 1–3 последовательно для первых 14, 15 и 16 значений.
В результате мы получаем таблицу, содержащую ex post прогнозы и соответствующие ошибки для последних четырех кварталов (табл..2).
Таблица 2
Ex post прогнозы для второй группы данных
| Исходная группа | Уравнение тренда | Ex post прогноз на следующий квартал | Исходные данные | Ошибка (абсолютная) Sабс |
| Первые 13 кварталов | ŷ = 196,31 + 5,824t | (на 14-й квартал) ŷ = 277,85 | y14 = 265 | -12,85 |
| Первые 14 кварталов | ŷ = 198,14 + 5,457t | (на 15-й квартал) ŷ = 280 | y15 = 268 | -12 |
| Первые 15 кварталов | ŷ = 199,74 + 5,157t | (на 16-й квартал) ŷ = 282,25 | y16 = 270 | -12,25 |
| Первые 16 кварталов | ŷ = 201,27 + 4,887t | (на 17-й квартал) ŷ = 284,35 | y17 = 248 | -36,35 |
Ex post прогноз на 16-й квартал (см. 3-ю строку табл. 2) получается, например, следующим образом: определяем с помощью какого-нибудь статистического пакета уравнение тренда для первых 15 кварталов. В полученное уравнение ŷ = 199,74 + 5,157t подставляем t = 16. Получаем значение 282,25 и сравниваем его с исходным значением, равным 270. Полученная ошибка S = –12,25.
Абсолютная среднеквадратическая ошибка равна: :
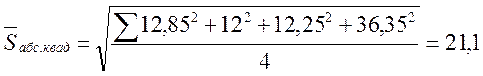
Проанализируем результаты работы: Если посмотреть на 2-й столбец табл. 2, то можно увидеть, что уравнение линии тренда каждый раз менялось. В этом нет ничего удивительного, поскольку уравнение линии тренда определяется полным набором данных. При изменении этого набора естественно изменялось и само уравнение.
В процессе ex post прогнозирования, добавляя новые данные, мы каждый раз получали другое уравнение!
Вся проблема заключается в том, насколько значительной была тенденция к изменению уравнения тренда, т. е. насколько стабильнымиоказались коэффициенты линейной модели при изменении набора данных. Проследим динамику изменения коэффициентов уравнений тренда.
Таблица 3
Динамика изменения коэффициентов уравнений тренда
| Исходная группа | a | b |
| Первые 13 кварталов | 196.31 | 5,824 |
| Первые 14 кварталов | 198.14 | 5,457 |
| Первые 15 кварталов | 199.74 | 5,157 |
| Первые 16 кварталов | 201.27 | 4,887 |
По данным таблицы 3 видно, что, в то время как коэффициенты a возрастают, коэффициенты b убывают. Это означает, что каждый раз при добавлении нового значения прямая линия становится более пологой, т. е. происходит замедление роста данных. В таком случае прогнозист, должен испытать на ex post другую модель, которая отображала бы процесс замедления роста, например квадратичную или логарифмическую.
Дата добавления: 2016-04-06; просмотров: 3113;
