Тестирование трендовых моделей с помощью ex post прогнозирования
Для оценки ошибок ex post прогнозов используется также число, которое называется коэффициентом несоответствияТейла.
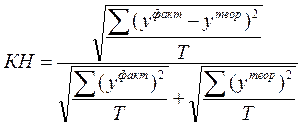
где Т — число ex post прогнозов.
а) Для линейного тренда коэффициент несоответствияТейларавен:
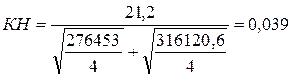
| уфакт | (уфакт)2 | утеор | (утеор)2 |
| 277,85 | 77200,62 | ||
| 282,25 | 79665,06 | ||
| 284,35 | 80854,92 | ||
| сумма | - | 316120,6 |
б) Рассмотрим параболический тренд: y=a+bt+ct2
Таблица 4
Ex post прогнозы для второй группы данных
| Исходная группа | Уравнение тренда | Ex post прогноз на следующий квартал | Исходные данные | Ошибка (абсолютная) Sабс |
| Первые 13 кварталов | ŷ = 188,16 + 9,083t-0,233 t2 | (на 14-й квартал) ŷ = 269.63 | y14 = 265 | -4,63 |
| Первые 14 кварталов | ŷ = 187,15 + 9,578t-0,275 t2 | (на 15-й квартал) ŷ = 268.94 | y15 = 268 | -0,94 |
| Первые 15 кварталов | ŷ = 186,95+ 9,672t-0,282 t2 | (на 16-й квартал) ŷ = 269.51 | y16 = 270 | +0,49 |
| Первые 16 кварталов | ŷ = 187,05 + 9,628t-0,2789 t2 | (на 17-й квартал) ŷ = 270.39 | y17 = 248 | -22,39 |
● Абсолютная среднеквадратическая ошибка равна: :
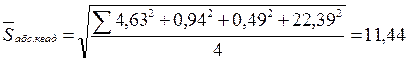
● Коэффициент несоответствия Тейла равен:
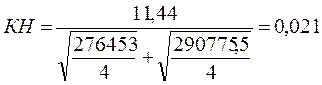
| уфакт | (уфакт)2 | утеор | (утеор)2 |
| 269,63 | 72700,34 | ||
| 268,94 | 72328,72 | ||
| 269,51 | 72635,64 | ||
| 270,39 | 73110,75 | ||
| сумма | - | 290775,5 |
б) Рассмотрим логарифмический тренд:y=a+b•lnt
Таблица 4
12
Дата добавления: 2016-04-06; просмотров: 918;
