Криволинейная и множественная корреляции.

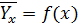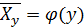Если график регрессии или изображается кривой линией, то корреляцию называют криволинейной. Например:

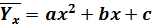(параболическая корреляция второго порядка).

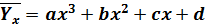(параболическая корреляция третьего порядка).

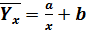(гиперболическая корреляция).

Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи). Независимые параметры уравнения регрессии ищут МНК.

Для оценки тесноты нелинейной корреляционной связи вводят новые сводиные характеристики:

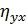-выборочное корреляционная отклонение Y к X.

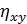-выборочное корреляционная отклонение X к Y.

Выборочным корреляционным отклонением Y, X называют отклонение линогруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y.

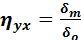или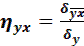

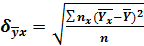
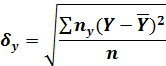
n- объём выборки 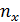- частота значений Х признак Х

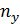- частота значений у признаки Y; 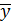- общее средняя признака X

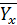- условная средняя признаки Y

Свойство 1. Корреляционное отношение удовлетворяет двойному неравенству

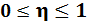
Свойство 2. Если 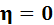, то и признак Y с признаком X корреляционной зависимостью не связан.

Свойство 3. Если 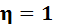,то признак Y связан с признаком X н функциональной зависимостью.

Свойство 4. Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корреляции

Свойство 5. Если выборочное корреляционное отношение равное абсолютной величине выборочного коэффициента корреляции, то имеет место линейная корреляционная зависимость.

Если исследуется связь между несколькими признаками, то корреляцию называют множественной. В простейшем случае число признаков равно трем, и связь между ними линейная.

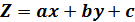
В этом случае возникают задачи:

1) найти по данным наблюдений выборочное уравнение связи вида:

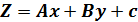т.е. требуется найти А, В, С.

2) оценить тесноту связи между Z и обоими признаками X и Y

3) оценить тесноту связи между Z и X (при постоянном Y) между Z и Y (при постоянном X).