Интервальные оценки. Доверительный интервал.
Интервальной называют оценку, которая определяется двумя числами — концами интервала. Интервальные оценки позволяют установить точность и надежность оценок
Пусть найденная по данным выборки статистическая характеристика 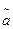 служит оценкой неизвестного параметра а. Ясно, что
служит оценкой неизвестного параметра а. Ясно, что 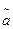 тем точнее определяет параметр а, чем меньше абсолютная величина разности
тем точнее определяет параметр а, чем меньше абсолютная величина разности 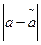 . Другими словами, если
. Другими словами, если 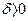 и
и 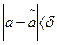 , то чем меньше
, то чем меньше  , тем оценка точнее. Таким образом, положительное число
, тем оценка точнее. Таким образом, положительное число  характеризует точность оценки.
характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка 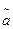 удовлетворяет неравенству
удовлетворяет неравенству 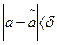 .Можно лишь говорить о вероятности j, с которой это неравенство осуществляется.
.Можно лишь говорить о вероятности j, с которой это неравенство осуществляется.
Доверительной вероятностью (надежностью) оценки а по 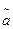 называют вероятность j, с которой осуществляется неравенство
называют вероятность j, с которой осуществляется неравенство 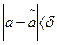
Обычно надежность задается наперед, причем в качестве j берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
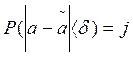 или
или 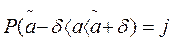
Доверительным называют интервал 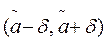 , который покрывает неизвестный параметр с заданной доверительной вероятностью.
, который покрывает неизвестный параметр с заданной доверительной вероятностью.
Доверительные интервалы для оценки МОЖ нормального распределения при известной 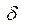 .
.
Пусть 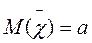 ;
; 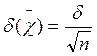 .
.
Попробуем чтобы вероятность 
Пользуясь формулой (лекция 3 вопрос 4)
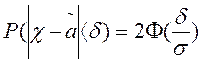
Заменив 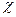 через
через 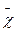 и
и 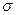 через
через 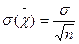 , получим
, получим 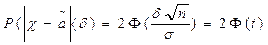 , где
, где  .
.
Найдя из последнего равенства  , можем написать
, можем написать
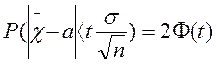
Смысл полученного соотношения таков: с надежностью j можно утверждать, что доверительный интервал 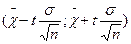 покрывает неизвестный параметр а; точность оценки
покрывает неизвестный параметр а; точность оценки 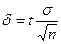 .
.
Если требуется оценить МОЖ с наперед заданной точностью S и надежностью j, то минимальный объем выборки, который обеспечит эту точность находят по формуле 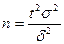 (следствие равенства
(следствие равенства 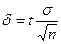 ).
).
Доверительные интервалы для оценки МОЖ нормального распределения при неизвестной  .
.
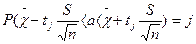
По таблице по заданным 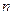 и
и 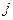 находим
находим 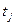 .
.
Для распределения Стьюдента.
S - исправления СКО; n – объем выборки.
При 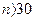 вместо распределения Стьюдента можно пользоваться нормальным распределением.
вместо распределения Стьюдента можно пользоваться нормальным распределением.
Доверительные интервалы для оценки среднего квадратического отклонения 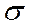 нормального распределения
нормального распределения

 S - исправленное СКО; q – находим по таблице
S - исправленное СКО; q – находим по таблице
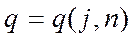
Тема 7. Элементы теории корреляции.
Дата добавления: 2016-03-05; просмотров: 1161;
