ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ
1. Пусть известно, что сл. величина x подчиняется нормальному закону с неизвестным средним μ и известной σ2 : X~N(μ,σ2), σ2 задано, μ не известно. Задано β. По выборке x1, x2, … , xn надо построить Iβ (θ) (сейчас θ=μ), удовлетворяющий (13)
Выборочное среднее (говорят также выборочная средняя) 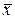 подчиняется нормальному закону с тем же центром μ, но меньшей дисперсией X~N (μ , D
подчиняется нормальному закону с тем же центром μ, но меньшей дисперсией X~N (μ , D 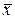 ), где дисперсией D
), где дисперсией D 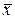 =σ2
=σ2 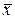 =σ2/n.
=σ2/n.
Нам понадобится число Кβ , определяемое для ξ~N(0,1) условием
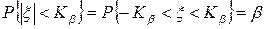
Словами: между точками -Кβ и Кβ оси абсцисс лежит площадь под кривой плотности стандартного нормального закона, равная β
Например, К0,90 =1,645 квантиль уровня 0,95 величины ξ
K0,95 = 1,96. ; К0,997=3 .
В частности, отложив от центра любого нормального закона 1,96 стандартных отклонений вправо и столько же влево, мы захватим площадь под кривой плотности, равную 0.95, в силу чего К0 95 является квантилью уровня 0,95 + 1/2*0,005 = 0,975 для этого закона.
Искомый доверительный интервал для генерального среднего μ есть IА(μ) = (х-σ, х+σ),
где δ = 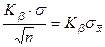 (15)
(15)
Дадим обоснование:
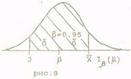
По сказанному, сл. величина 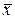 в интервал J=μ±σ попадает с вероятностью β (рис.9). В этом случае величина
в интервал J=μ±σ попадает с вероятностью β (рис.9). В этом случае величина 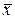 отклоняется от центра μ меньше, чем на δ , и случайный интервал
отклоняется от центра μ меньше, чем на δ , и случайный интервал 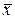 ± δ (со случайным центром
± δ (со случайным центром 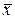 и такой же как у J ширины) накроет точку μ. То есть
и такой же как у J ширины) накроет точку μ. То есть 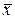 Є J <=> μ Є Iβ , а потому Р{μЄІβ} = Р{
Є J <=> μ Є Iβ , а потому Р{μЄІβ} = Р{ 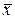 Є J }=β.
Є J }=β.
Итак, постоянный по выборке интервал Iβ содержит среднее μ с вероятностью β.
Ясно, чем больше n, тем меньше σ 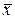 и уже интервал, а чем больше мы берем гарантию β, тем доверительный интервал шире.
и уже интервал, а чем больше мы берем гарантию β, тем доверительный интервал шире.
Пример 21.
По выборке с n=16 для нормальной величины с известной дисперсией σ2=64 найдено х=200. Построить доверительный интервал для генерального среднего (иначе говоря, для математического ожидания) μ, приняв β=0,95.
Решение. I β(μ)= 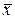 ± δ, где δ = Кβσ/
± δ, где δ = Кβσ/  -> Кβσ/
-> Кβσ/  =1.96*8/
=1.96*8/ 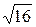 = 4
= 4
I0.95(μ)=200  4=(196;204).
4=(196;204).
Делая вывод, что с гарантией β=0,95 истинное среднее принадлежат интервалу (196,204), мы понимаем, что возможна ошибка.
Из 100 доверительных интервалов I0. 95 (μ) в среднем 5 не содержат μ.
Пример 22.
Каким в условиях предыдущего примера 21 следует взять n, чтобы вдвое сузить доверительный интервал? Чтобы иметь 2δ=4, надо взять 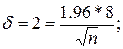
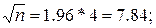
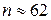
На практике часто пользуются односторонними доверительными интервалами. Так, если полезны или не страшны высокие значения μ, но не .приятны низкие, как в случае с прочностью или надежностью, то резонно строить односторонний интервал. Для этого следует максимально поднять его верхнюю границу. Если мы построим, как в примере 21, двусторонний доверительный интервал для заданного β, а затем максимально расширим его за счет одной из границ, то получим односторонний интервал с большей гарантией β' = β + (1-β) / 2 = (1+β)/2, например, если β = 0,90, то β = 0,90 + 0,10/2 = 0,95.
Например, будем считать, что речь идет о прочности изделия и поднимем верхнюю границу интервала до 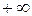 . Тогда для μ в примере 21 получим односторонний доверительный интервал (196,°°) с нижней границей 196 и доверительной вероятностью β'=0,95+0,05/2=0,975.
. Тогда для μ в примере 21 получим односторонний доверительный интервал (196,°°) с нижней границей 196 и доверительной вероятностью β'=0,95+0,05/2=0,975.
Практическим недостатком формулы (15)_является то, что она выведена в предположении, что дисперсия 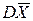 = σ2 (отсюда и
= σ2 (отсюда и 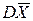 = σ2/n) известна; а это бывает в жизни редко. Исключение составляет случай, когда объем выборки велик, скажем, n измеряется сотнями или тысячами и тогда за σ2 можно практически принять ее оценку s2 или
= σ2/n) известна; а это бывает в жизни редко. Исключение составляет случай, когда объем выборки велик, скажем, n измеряется сотнями или тысячами и тогда за σ2 можно практически принять ее оценку s2 или  .
.
Пример 23.
Положим, в некотором большом городе в результате выборочного обследования жилищных условий жителей получена следующая таблица данных (пример из работы [6]).
Таблица 8
Исходные данные к примеру
| Общая (полезная) | До | 5.0- | 10.0- | 15.0- | 20.0- | 25.0- | Более |
| площадь жилищ, | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 | 30.0 |
| приходящаяся на | |||||||
| 1 человека, м | |||||||
| Число жителей |
Естественно допустить, что сл. величина X - общая (полезная) площадь (в м2), приходящаяся на одного человека подчиняется нормальному закону. Среднее μ и дисперсия σ2 не известны. Для μ требуется построить 95%-ный доверительный интервал. Чтобы по группированным данным найти выборочные средние и дисперсию, составим следующую таблицу выкладок (табл.9).
Таблица 9
Вычисления X и 5 по сгруппированным данным
| N группы з | Общая площадь в расчете на 1 человека, м2 | Число жителей в группе гj | Середина интервала xj | rjxj | rjxj2 |
| До 5.0 | 2.5 | 20.0 | 50.0 | ||
| 5.0-10.0 | 7.5 | 712.5 | 5343.75 | ||
| 10.0-15.0 | 12.5 | 2550.0 | 31875.0 | ||
| 15.0-20.0 | 17.5 | 4725.0 | 82687.5 | ||
| 20.0-25.0 | 22.5 | 4725.0 | 106312.5 | ||
| 25.0-30.0 | 27.5 | 3575.0 | 98312.5 | ||
| более 30.0 | 32.5 * | 2697.5 | 87668.75 | ||
| - | 19005.0 | 412250.0 |
В этой вспомогательной таблице по формуле (2) подсчитаны первый и второй начальные статистические моменты а1 и а2
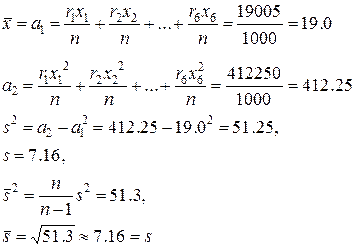
Хотя дисперсия σ2 здесь неизвестна, из-за большого объема выборки можно практически применить формулу (15), положив в ней σ= 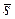 =7.16.
=7.16.
Тогда δ=k0.95σ/  =1.96*7.16/
=1.96*7.16/ 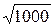 =0.46.
=0.46.
Доверительный интервал для генерального среднего при β=0,95 равен I0.95 (μ) = 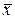 ± δ = 19 ± 0.46 = (18.54; 19.46).
± δ = 19 ± 0.46 = (18.54; 19.46).
Следовательно, среднее значение площади на одного человека в данном городе с гарантией 0.95 лежит в промежутке (18.54; 19.46).
2. Доверительный интервал для математического ожидания μ в случае неизвестной дисперсии σ2 нормальной величины. Этот интервал для заданной гарантии β строится по формуле 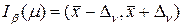 ,где ν = n-1 ,
,где ν = n-1 ,
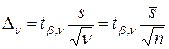 (16)
(16)
Коэффициент tβ,ν имеет тот же смысл для t – распределения с ν степенями свободы, что кβ для распределения N(0,1), а именно:
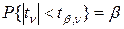 .
.
Другими словами, сл. Величина tν попадает в интервал (-tβ,ν; +tβ,ν) с вероятностью β. Значения tβ,ν даны в табл.10 для β=0.95 и β=0.99.
Таблица 10.
Значения tβ,ν
| Число степеней ν | 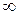
| |||||||
| t0.95,ν | 4.3 | 2.57 | 2.23 | 2.13 | 2.09 | 2.04 | 2.00 | 1.96 |
| t0.99,ν | 9.92 | 4.03 | 3.17 | 2.95 | 2.84 | 2.75 | 2.66 | 2.576 |
Возвращаясь к примеру 23, видим, что в нем доверительный интервал был построен по формуле (16) с коэффициентом tβ,υ=k0..95=1.96, т. к. n=1000.
Пример 24.Построить 99%-ный доверительный интервал для генерального среднего диаметра Д валика по "пробе" из 10 деталей, сработанных на токарном автомате, если отклонения х1 размеров этихваликов от номинального размера оказались следующими (в мк): 2, 1, -2, 3, 2, 4, -2, 5, 3, 4; n=10.
Находим 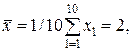
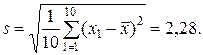
Строим доверительный интервал для среднего μ (отсчитываемого также от номинального размера) из условия
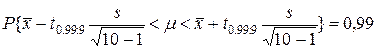 .
.
В таблице 10 для числа степеней свободы ν=10-1=9 1%-ный предел t0.99:9 отсутствует, есть для ν=5 и для ν=10: t0.99:5=4,03; t0.99:10=3,17. Линейная интерполяция дает t0.99:9= 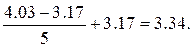 Откуда
Откуда 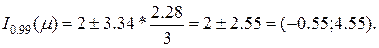
Таким образом, согласующиеся с нашими опытными данными, иными словами, "допустимые" (с гарантией 99%) значения параметра μ лежат в интервале (-0.55, 4.55). Если коэффициент 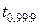 получать не интерполяцией, а из более подробных таблиц, то найдем точнее
получать не интерполяцией, а из более подробных таблиц, то найдем точнее 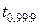 =3.25 и интервал Iβ(μ) будет чуть уже.
=3.25 и интервал Iβ(μ) будет чуть уже.
Заметим, что если бы мы приняли число s=2.28 за значение параметра б и применим формулу, 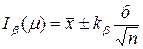 то "классические" 99%-ные доверительные границы были бы значительно уже. В самом деле, вместо
то "классические" 99%-ные доверительные границы были бы значительно уже. В самом деле, вместо 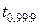 =3,34 мы бы взяли
=3,34 мы бы взяли  =2,58 и получили δ=
=2,58 и получили δ= 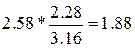 , т.е. оказалось бы
, т.е. оказалось бы 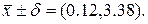 Этим мы значительно преувеличили бы действительную точность нашей оценки.
Этим мы значительно преувеличили бы действительную точность нашей оценки.
Дата добавления: 2016-02-27; просмотров: 1969;
