ВАЖНЕЙШИЕ ХАРАКТЕРИСТИКИ ВЫБОРКИ
Пусть мы имеем выборку (х1; x2,...,хn ) объема n. Для инженера это значит, что мы сделали случайный отбор n элементов из генеральной совокупности, математик же предпочитает говорить, что мы провели n независимых наблюдений над случайной величиной X, подчиненной некоторому (известному, а чаще нет) закону. Точки х1; x2,...,хn - реализации cл. величины Х - записаны в порядке их получения (в хронологической порядке).
Если эти числа записать иначе, в порядке возрастания х1 < х2 <. . .xn, то получим упорядоченную выборку, называемую еще вариационным рядом.
Расстояние хn – х1 между крайними членами этого ряда называется размахом вариационного ряда. эта характеристика рассеяния, разброса случайной величины.
Пример 1. Имеем выборку из нормального стандартного закона:
{0.414; -0.011; 0.666; -1.132; -0.410; -1.077; 0.734;}
число точек (объем выборки) n=7. Переставляя числа по возрастанию, получим упорядоченную выборку:
{-1.132; -1.077; -0.410; -0.011;0.414; 0.666; 0.743}.
Размах равен 0.734-(-1.132)=2.866.
x1 =0.414 - первый элемент выборки, х(1)=-1.132 - первый элемент вариационного ряда, аналогично x2 =-0.011, х(2)'=-1.077.
В большинстве задач выборка и вариационный ряд несут одинаковую информацию, но с вариационным рядом легче работать в силу его упорядоченности. Все же некоторая потеря информации при упорядочивании происходит: по вариационному ряду нельзя судить о независимости наблюдений, т.е. о случайности выборки.
Рассмотрим какой-либо вариационный ряд.
---- * ----*---- * ------ * -----* ----* -----* ---- * ----- * -------------------------
x(1) x(3) d=x(5) x(9) x
Рис.1
Найдем такую точку х на оси абсцисс, что справа и слева от нее будет одинаковое число точек выборки. Если число n точек выборки нечетно , то х совпадет с точкой x(n+1)/2 вариационного ряда. Обозначим эту точку d и назовем медианой выборки. Когда же n четно, то указанных точек х, делящих выборку пополам, много, а из них нам в качестве медианы нужна одна. Чтобы ее найти, возьмем по одной ближайшей слева и справа к точке х точке ряда и за медиану примем среднее значение между ними.
Если для характеристики выборки как целого нам нужно выбрать несколько чисел, которые легко найти, то ими окажутся:
а) крайние точки - наибольшее и наименьшее х(n) и х(1)
б) срединное значение - медиана d.
Если мы хотим добавить еще два числа, образовав 5-числовую сводку, то естественно поступить так; мысленно отбросим точки выборки справа от медианы d и найдем медиану для оставшихся точек, назвав ее нижней квартилью выборки. Аналогично, верхняя квартиль находится как медиана для части выборки, остающейся при удалении точек слева от d. (Кварта - от латинск. quarta - четверть).
Пример 2. Дать 5-числовую сводку по выборке с n=13; -1.7;
{-0.4; 1.5; -3.2; 1.2; 0.3; 1.8; 3.0; 2.4; 4.3; 9.8, 6.4; 0.1.}
Вариационный ряд {-3.2; -1.7; -0.4; 0.1; 0.3; 1.2; 1.5; 1.8;
2.4; 3.0; 4.3. 6.4. 9.8.}
Медиана d=x(7)=1.5, а квартили - четвертое число от каждого конца, т.е. 0.1 и 3.0. 5-числовая сводка: -3.2; 0.1; 1.5; 3.0;
9.8.
Известный американский статистик Дж.Тыоки рекомендует такой ряд изображать в виде;
-3.2 1.5 9.8
-1.7 1.2 1.8 6.4
-0.4 0.3 2.4 4.3
0.1 3.0
а 5-числовую сводку ряда в виде схемы:

Пример 7. О чем нам говорит 5-числовая сводка:

Решение. Все 1000 наблюдений лежат на числовой оси между 10 и 500, причем неравномерно, половина слева от медианы d=70, половина справа.
Левее нижней квартили х=30 и правее верхней х=150 лежит по четвертой части всех наблюдений, а между ними половина, т.е. в каждом промежутке [10,30], [30,70], [70,150] и [150,500] лежит по 250 наблюдений.
Следует помнить, что теоретическая или истинная медиана d (медиана генеральной совокупности) является неслучайным числом, определяемым по закону распределения условием:
P(x>d)=P(x<d). Выборочная же медиана d является случайной величиной; для разных выборок из одной генеральной совокупности она примет хотя и близкие, но разные значения.
Статистическое распределение выборки - это таблица из двух строк. В верхней указаны в порядке возрастания наблюдаемые значенияx1 (их называют вариантами), а под ними указаны соответствующие им частоты (называемые также относительными частотами, т.е. числа наблюдений, деленные на n - объем выборки).
Пример 3. Имея конкретную выборку: {2, 6, 12, 6, 6, 2,6, 12, 12, 6, 6, 6, 12, 12, 6, 12, 2, 6, 12, 6 }(n=20) - записать вариационный ряд и статистическое распределение выборки.
Ваоиационный ряд: {2, 2, 2, 6, 6, б, 6, б, б, 6, 6, 6, 6, 12,
12, 12, 12, 12, 12, 12}.
Статистическое распределение выборки объема n=20.
Контроль: 0.15+0.5+0.35=1.
| варианты x'1 | |||
| частоты Р1 | 0.15 | 0.5 | 0.35 |
Заметим что в выборке могут быть совпадающие числа, тогда как варианты- несовпадающие числа, число их обычно меньше n.
Статистические моменты. При проведении статистического исследования истинными (или теоретическими) являются характеристики генеральной совокупности. Именно их хотел бы знать исследователь. тогда как на деле по выборке он вычисляет эмпирические характеристики - характеристики выборки.
Если формуму
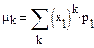
применяемую для вычисления начального момента К-го порядка дискретной cл.величины, применить к статистическому распределению (заменив вероятности p1 на частоты 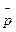 1, то получим x’
1, то получим x’
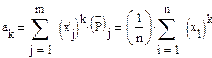
-статистический (или эмпирический) начальный момент К-го порядка; m - число вариант x'1 .
В частности,
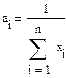
- выборочное среднее, его обозначают 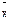 .
.
Наряду с начальными моментами употребляют и центральные:
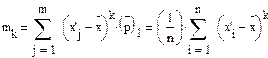
статистический центральный момент к-го порядка. Особенно важен второй:
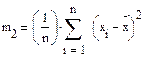
- выборочная дисперсия. Ее обозначают S2 .
Пример 9. По упорядоченной выборке:{ 4,6,7,7,10,15,18 }(m=7) найти первый и второй начальные статистические моменты и второй центральный.
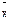 = a = (4+б+7+7+10+15+18)/7 = 9.57.
= a = (4+б+7+7+10+15+18)/7 = 9.57.
a2 = (42+62+72+72+102+15Z+182)/7 = (16 +36 + 49 *49 + 100+ 225 + 324)/7 = 799/7 = 114,14.
S2 = m2 = (1/7)(4-9.57)2 + (6-9.57)2 + (7-9.57)2 + (7-9.57)2 + (10-9.57)2 + (15-9.57)2 + (18-9.57)2 = (1/7)[31.02 * 12.74 + 6.60 + 6.60 + 0.18 + 29.48 + 71.06] = 157.68/7 = 22.52.
Полезной как для вычислений, так и для контроля служит формула для S2, эквивалентная предыдущей и имеющая вид:
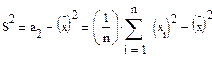 (3)
(3)
В нашем примере S2 = 114.14 - 9.572 = 114.14 - 91.58 = 22.56. С ошибкой в последнем знаке выборочные дисперсии, найденные по двум формулам, совпадают. Заметим, что из-за ошибки округления вторая формула для S2 требует для получения той же точности делать вычисления с большим (на 1 или 2) числом знаков.
УПРАЖНЕНИЯ.
Доказать тождество
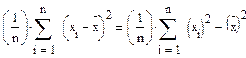
2. Доказать, что:
а) при увеличении каждого элемента Xi выборки на 10 выборочное среднее х увеличится на 10, a S2 не изменится.
б) при увеличении каждого элемента х1 выборки в 10 раз х среднее также возрастет в 10 раз, а дисперсия S2 в 100 раз.
В теории вероятностей употребляются характеристикизаконараспределения:

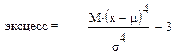
Деление на среднеквадратическое в соответствующей степени делает эти характеристики безразмерными. Асимметрия равна нулю для симметричных распределений, она больше нуля, если "хвост" распределения тянется вправо.
У нормального распределения асимметрия и эксцесс нулевые. Если эксцесс больше нуля, это, как правило, означает, что график плотности в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. Для более плосковершинных, чем нормальное, распределений эксцесс отрицателен.
По выборке мы находим приближенные значения асимметрии и эксцесса, строим оценки:
асимметрия выборки = m3/ S3 (4)
эксцесс выборки = m4/ s4 - 3 (5)
Когда наблюдения проводятся над системой (Х,У) двух случайных величин, то выборка состоит уже из пар чисел - значений Хи У: ( x1.,yi), (х2 , y2 ),.... (хn , yn ). Поxiмы можем построить рассмотренные статистические моменты для X, по уi - для У. Связь между X и У, точнее, меру близости этой связи к линейной, выражает коэффициент корреляции:
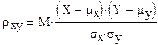
Заменой средних μx μy на выборочные средние и дисперсий
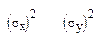 на выборочные дисперсии
на выборочные дисперсии 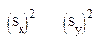 получим оценку дляρxy-выборочный коэффициент корреляции rxy:
получим оценку дляρxy-выборочный коэффициент корреляции rxy:
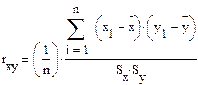 (6)
(6)
Эту формулу легко преобразовать к виду:
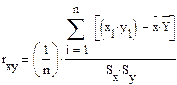
Как иρxy, выборочный коэффициент корреляции rxy заключен между -1 и +1. Если rxy =±1, то точки (х1 ,у1 ) лежат строго на прямой, т.е. имеет место строгая линейная зависимость.
Пример 10. Испытана рессорная сталь на прочность прикручении и изгибе. Х - прочность при кручении, У - прочность приизгибе; (x1, y1 ) - прочность при кручении и изгибе i-ro образца стали.
Вычислить выборочный коэффициент корреляции rxy по выборке объема n=12, заданной в двух столбцах таблицы 3.
Таблица 3
Вычисление гxy
| N | X1 | У1 | ∆X | ∆y | (∆X)2 | (∆Y)2 | (∆X) ∆Y |
| исп. | |||||||
| -37 | -21 | ||||||
| -21 | -16 | ||||||
| -4 | -3 | ||||||
| -7 | -2 | ||||||
| -17 | -3 | ||||||
| Q | |||||||
| -1 | -3 | ||||||
| -2 | -2 | ||||||
| ∑ | -1 |
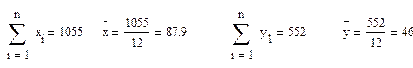
∆x обозначает разность  , а ∆у обозначает
, а ∆у обозначает 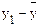 .
.
Сумма чисел в столбцах ∆x и ∆y теоретически должна всегда равняться нулю. В столбце ∆x сумма оказалась равной -1 (ане 0), потому что вместо точного значения х=87.9 было использовано округленное значение 88.
Выборочные дисперсии:
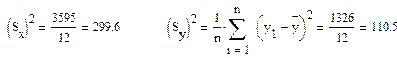
Выборочный коэффициенткорреляции:
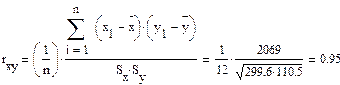
Как видим, в среднем прочность на кручение почти вдвое больше, чем при изгибе.
Близость коэффициента корреляции к 1 говорит о практически линейной связи между Х и У.
Статистические моменты вычисляются по случайной выборке и потому являются сл. величинами. Поэтому следует различать две вещи:
1) статистический момент как cл. величину и 2) конкретное значение этого момента, наблюденное по конкретной выборке. Для определенности рассмотрим выборочное среднее. Его следовало бы обозначить среднее X, когда выборочное среднее есть cл. величина, и обозначить среднее х, когда мы говорим о реализации х, т.е. о среднем арифметическом значении элементов конкретной выборки.
Точно так же и выборку, строго говоря, следует понимать в двух смыслах: 1) как систему (Х1 ,X2 , ...,Хn) n независимых одинаково распределенных cл. величин, у каждой из которых закон распределения тот же, что у cл. величины X, над которой проводятся наблюдения, и 2) как конкретную выборку x1 , x2,... xn, где x1 реализация cл. величины Х1 , ....xn -реализация величины Хn.
Выясним, какому закону подчиняется выборочное среднее Х=Хn, если наблюдения проводятся над нормальной cл. величиной
Как сумма нормальных величин X1+Х2+...+Хn,
числитель величины 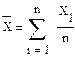 подчиняется нормальному закону. Найдем математическое ожидание и дисперсию величины «среднее X»
подчиняется нормальному закону. Найдем математическое ожидание и дисперсию величины «среднее X»
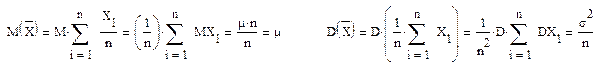
Таким образом 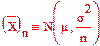 (8)
(8)
Интуитивно ясно, что если взять ряд выборок (из n элементов каждая), то средние этих выборок должны вести себя куда более стабильно, чем исходная сл. величина X: меньше отклоняться μ и меньше "прыгать" от одной выборки к другой. Формула (8) это подтверждает: у величины среднее X тот же центр μ распределения, но дисперсия в n раз меньше: б2x- = б2/n.
Пример. Каким следует взять объем выборки п, чтобы выборочное среднее подчинялось закону N(μ,0.1), если Х ~ N(μ,5)?
0.1 = DX = б2x-= 5/n, n=5/0.1=50.
По поводу формулы (8) надо добавить следующее. Соотношения MX = MX и DX = DX/n выведены без учета требования нормальности.
Если число наблюдений n велико, то каким бы ни было распределение у X, в силу центральной предельной теоремы выборочное среднее Хn подчиняется закону, близкому к нормальному; тем более близкому, чем больше n и чем ближе к нормальному закон распределения величины X. Так что формула (8) приближенно верна всегда.
С ростом объема n выборки плотность вероятности для среднее Хn концентрируется около центра μ и имеет нормальный вид, высота графика плотности пропорциональна n1/2
Дата добавления: 2016-02-27; просмотров: 1127;
