ИНТЕРВАЛЬНАЯ ОЦЕНКА ВЕРОЯТНОСТИ

Пусть испытания проводятся по схеме Бернулли, т.е. событие А наступает в единичном испытании с некоторой вероятностью р и испытания независимы.

Число наступления А в n испытаниях (кратко: число успехов) обозначаем Х.

Как известно, это - биномиальная сл. величина со средним МХ=nр и дисперсией DХ =npq. Точечной оценкой неизвестной вероятности р=Р(А) служит частота успехов 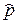=Х/n. Например, если величина X приняла конкретное значение m=7 в 10 испытаниях, то частота успехов 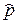=m/n=7/10.

Теперь мы хотим найти доверительный интервал I_β(p) Для неизвестной вероятности р. Ограничимся приближенным решением (из-за его простоты). В силу центральной предельной теоремы при большом числе испытаний величины X и 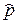=Х/n подчиняются закону, близкому к нормальному:

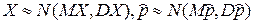, где ,

.

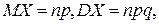
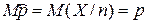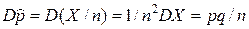Если мы имеем одно наблюдение над какой-то нормальной сл.величиной Z~ 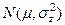, то для ее математического ожидания μ доверительный интервал мы можем построить как 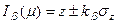- Теперь же этой величиной Z является частота 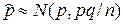и в последней формуле надо μ заменить на р, Z на 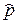, б_z на .

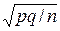Тогда получим .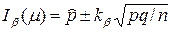

К сожалению, член pq/n нам неизвестен и мы вынуждены заменить его оценкой 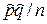, что приводит к окончательной формуле

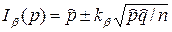(17)

Эта формула приближенная, она хороша при условии, что величина npq велика (скажем, когда npq>10).

Пример 25.

Дано, что из 1000 наугад взятых жителей одного города число людей, имеющих на 1-го человека жилую площадь 15 м², составляет 8+95+204=307, т.е. 30,7%.

Оценим долю р людей в этом городе, имеющих площадь меньше 15м².

Дано n=1000, 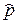=0.307, β=0,95. К_β=К_0.95=1.96.

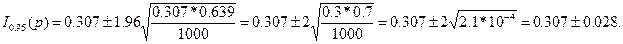
I_0.95(p)=(0.28; 0.335) - доля жителей города, имеющих указанную жилплощадь, заключена между 0,28 и 0,34 с гарантией 0,95. Смысл гарантии 0,95 в том, что, беря другие сл. выборки жителей в том же или ином городе и строя подобные же доверительные интервалы, мы в 95% случаев построим верный интервал, а в 5% ошибочный, не накрывающий истинное значение интересующего параметра.

Пример 26.

Пусть частота 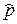безотказной работы при первых n испытаниях ракеты составила 0,96. Построить доверительный интервал для вероятности р безотказной работы ракеты в двух случаях х: а) n=1000, б) n=100.

Принять β=0.95

Решение.

а)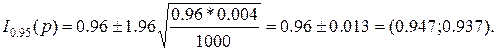

б)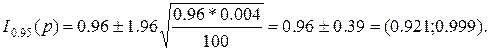

В случае б) доверительный интервал крайне груб, поскольку требование npq > 10 не выполнено: npq 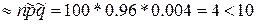и следует найти точный доверительный интервал для р, основанный на биноминальном распределении.