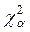ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ДВУХ ГЕНЕРАЛЬНЫХ СРЕДНИХ
Рассмотрим две независимые выборки x1, x2, ….. , xn и y1, y2 , … , yn, извлеченные из нормальных генеральных совокупностей с одинаковыми дисперсиями 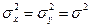 , причем объемы выборок соответственно n и m, а средние μx, μy и дисперсия σ2 неизвестны. Требуется проверить основную гипотезу Н0: μx=μy при конкурирующей Н1: μx
, причем объемы выборок соответственно n и m, а средние μx, μy и дисперсия σ2 неизвестны. Требуется проверить основную гипотезу Н0: μx=μy при конкурирующей Н1: μx 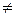 μy.
μy.
Как известно, выборочные средние 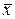 и
и 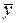 будут обладать свойствами:
будут обладать свойствами: 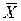 ~N(μx, σ2/n),
~N(μx, σ2/n), 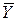 ~N(μy, σ2/m).
~N(μy, σ2/m).
Их разность 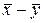 - нормальная величина со средним
- нормальная величина со средним 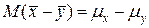 и дисперсией
и дисперсией 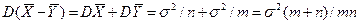 , так что
, так что
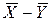 ~
~ 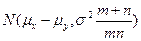 (23).
(23).
Допустим на время, что основная гипотеза Н0 верна: μx–μy=0. Тогда 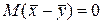 и, деля величину
и, деля величину 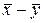 на ее стандартное отклонение, получим стандартную нормальную сл. Величину
на ее стандартное отклонение, получим стандартную нормальную сл. Величину 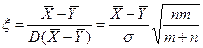 ~N(0,1).
~N(0,1).
Раньше отмечалось, что сл. величина 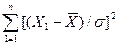 распределена по закону
распределена по закону 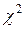 с (n-1)-ой степенью свободы, a
с (n-1)-ой степенью свободы, a 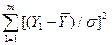 - по закону
- по закону 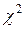 с (m-1) степенью свободы. С учетом независимости этих двух сумм, получаем, что их общая сумма
с (m-1) степенью свободы. С учетом независимости этих двух сумм, получаем, что их общая сумма 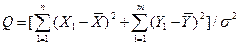 распределена по закону
распределена по закону 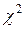 с n+m-2 степенями свободы.
с n+m-2 степенями свободы.
Вспоминая п.7, видим, что дробь 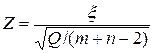 подчиняется t-распределенню (Стьюдента) с ν=m+n-2 степенями свободы: Z=t. Этот факт имеет место только тогда, когда истинна гипотеза Н0.
подчиняется t-распределенню (Стьюдента) с ν=m+n-2 степенями свободы: Z=t. Этот факт имеет место только тогда, когда истинна гипотеза Н0.
Заменяя ξ и Q их выражениями, получим развернутую форнулу для Z:
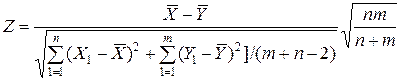 (24)
(24)
Сл.величина Z, называемая статистикой критерия, позволяет принять решение при такой последовательности действий:
1. Устанавливается область D=[-tβ,ν, +tβ,ν], содержащая β=1–α площади под кривой tν–распределения (табл.10).
2. Вычисляется по формуле (24) опытное значение Zon статистики Z, для чего вместо X1 и Y1 подставляются значения x1 и y1 конкретных выборок, а также их выборочные средние 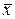 и
и 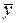 .
.
3. Если Zon 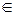 D, то гипотеза Н0 считается не противоречащей опытным данным и принимается.
D, то гипотеза Н0 считается не противоречащей опытным данным и принимается.
Если Zon 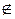 D, то принимается гипотеза Н1.
D, то принимается гипотеза Н1.
Если гипотеза Н0 верна, то Z подчиняется известному tν–распределению с нулевым средним и с высокой вероятностью β=1–α попадает в D-область принятия гипотезы Н0. Когда наблюдаемое, опытное значение Zon попадает в D. Мы рассматриваем это как свидетельство в пользу гипотезы Н0.
Когда жe Z0n лежит за пределами D (как говорят, лежит в критической области К), что естественно, если верна гипотеза Н1, но маловероятно, если верна Н0, то нам остается отклонить гипотезу Н0, приняв H1.
Пример 31.
Сравниваются две марки бензина: А и В. На 11 автомашинах одинаковой мощности по кольцевому шассе испытан по разу Бензин марки А и В. Одна машина в пути вышла из строя н для нее данные по бензину В отсутствуют.
Расход бензина в пересчете на 100 км пути
Таблица 12
| i | ||||||||||||
| Xi | 10,51 | 11,86 | 10,5 | 9,1 | 9,21 | 10,74 | 10,75 | 10,3 | 11,3 | 11,8 | 10,9 | n=11 |
| Уi | 13,22 | 13,0 | 11,5 | 10,4 | 11,8 | 11,6 | 10,64 | 12,3 | 11,1 | 11,6 | - | m=10 |
Дисперсия расхода бензина марок А и В неизвестна и предполагается одинаковой. Можно ли при уровне значимости α=0,05 принять гипотезу о том, что истинные средние расходы μА и μВ этих видов бензина одинаковы?
Решение. Проверку гипотезы Н0: μА-μВ=0 при конкурирующей. Н1:μ1 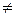 μ2 делаем по пунктам:
μ2 делаем по пунктам:
1. Находим выборочные средние 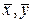 и сумму квадратов отклонений Q.
и сумму квадратов отклонений Q.
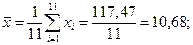
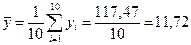 ;
;
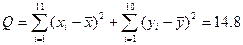 ;
;
2. Вычисляем опытное значение статистики Z
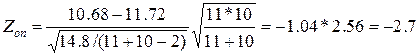
3. Находим из таблицы 10 t-распределения предел tβ,ν, для числа степеней свободы ν=m+n–2=19 и β=1–α=0.95. В таблице 10 есть t0.95.20=2,09 и t0.95.15=2,13, но нет t0.95.19. Находим интерполяцией t0.95.19=2,09+ 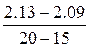 =2,10.
=2,10.
4. Проверяем, в какой из двух областей D или К лежит число Zon. Zon=-2,7 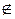 D=[-2,10; -2,10].
D=[-2,10; -2,10].
Поскольку наблюденное значение Zon лежит в критической области, К=R\D, то отбрасываем. Н0 и приникаем гипотезу Н1. В этом случае про 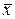 и
и 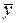 говорят, что их разность
говорят, что их разность 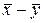 значима. Если бы при всех условиях этого примера изменилось бы лишь Q, скажем, Q вдвое возросло, то изменился бы и наш вывод. Увеличение Q вдвое привело бы к уменьшению в
значима. Если бы при всех условиях этого примера изменилось бы лишь Q, скажем, Q вдвое возросло, то изменился бы и наш вывод. Увеличение Q вдвое привело бы к уменьшению в 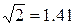 раза величины Zon и тогда число Zon попало бы в допустимую область D, так что гипотеза H0 выдержала бы проверку и была принята. В этом случае расхождение между
раза величины Zon и тогда число Zon попало бы в допустимую область D, так что гипотеза H0 выдержала бы проверку и была принята. В этом случае расхождение между 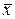 и
и 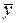 объяснялось бы естественным разбросом данных, а не тем, что μА
объяснялось бы естественным разбросом данных, а не тем, что μА 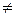 μВ.
μВ.
Теория проверки гипотез весьма обширна, гипотезы могут быть о виде закона распределения, об однородности выборок, о независимости сл.величины и т.д.
КРИТЕРИЙ c2 (ПИРСОНА)
Самый распространенный на практике критерий проверки простой гипотезы. Применяется, когда закон распределения неизвестен. Рассмотрим случайную величину X, над которой проведено n независимых испытаний. Получена реализация x1, x2,...,xn. Необходимо проверить гипотезу о законе распределения этой случайной величины.
Рассмотрим случай простой гипотезы. Простая гипотеза проверяет согласование выборки с генеральной совокупностью, имеющей нормальное распределение (известное). По выборкам строим вариационный ряд x(1), x(2), ..., x(n). Интервал [x(1), x(n)] разбиваем на подинтервалы. Пусть этих интервалов r. Тогда найдем вероятность попадания X в результате испытания в интервал Di, i=1 ,..., r в случае истинности проверяемой гипотезы.
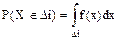
Критерий проверяет не истинность плотности вероятности, а истинность чисел
pi=P(XÎDi)
С каждым интервалом Di свяжем случайное событие Ai - попадание в этот интервал (попадание в результате испытания над X ее результата реализации в Di). Введем случайные величины. mi - количество испытаний из n проведенных, в которых произошло событие Ai. mi распределены по биномиальному закону и в случае истинности гипотезы
Mmi=npi
Dmi=npi(1-pi)
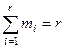
Критерий c2 имеет вид 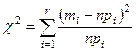
p1+p2+...+pr=1
m1+m2+...+mr=n
Если проверяемая гипотеза верна, то mi представляет частоту появления события, имеющего в каждом из n проведенных испытаний вероятность pi, следовательно, мы можем рассматривать mi как случайную величину, подчиняющуюся биномиальному закону с центром в точке npi. Когда n велико, то можно считать, что частота распределена асимптотически нормально с теми же параметрами. При правильности гипотезы следует ожидать, что будут асимптотически нормально распределены
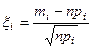
связанные между собой соотношением
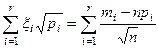
В качестве меры расхождения данных выборки m1+m2+...+mr с теоретическими np1+np2+...+npr рассмотрим величину
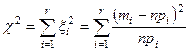
c2 - сумма квадратов асимптотически нормальных величин, связанных линейной зависимостью. Мы ранее встречались уже с аналогичным случаем и знаем, что наличие линейной связи привело к уменьшению на единицу числа степеней свободы.
Если проверяемая гипотеза верна, то критерий c2 имеет распределение, стремящееся при n®¥ к распределению c2 с r-1 степенями свободы.
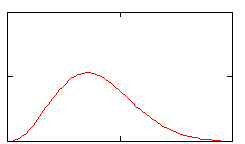
Допустим, что гипотеза неверна. Тогда существует тенденция к увеличению слагаемых в сумме, т.е. если гипотеза неверна, то эта сумма будет попадать в некую область больших значений c2. В качестве критической области возьмем область положительных значений критерия

|
В случае неизвестных параметров распределения каждый параметр уменьшает на единицу количество степеней свободы для критерия Пирсона
Дата добавления: 2016-02-27; просмотров: 1101;