МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ПРЯМОЙ ЛИНИИ
При обработке наблюдений широко применяется метод наименьших квадратов (МНК). Его суть изложим на частном примере прямой линии.
Пусть на плоскости хоу дано n точек: (х1 ; у1) , (х2; у2) , … , ( xn ; yn ).
Среди всех прямых линий у=ах+b на плоскости мы ищем наиболее близкую к данной системе точек, причем близость измеряем суммой S квадратов отклонений:
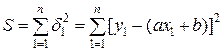 , (25)
, (25)
где 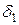 - отклонение вдоль оси y i–той точки от прямой [δ1>0, если точка (x1; y1) лежит над прямой ], S – сумма квадратов указанных отклонений по всем n точкам.
- отклонение вдоль оси y i–той точки от прямой [δ1>0, если точка (x1; y1) лежит над прямой ], S – сумма квадратов указанных отклонений по всем n точкам.
Из всех прямых наилучшей в смысле метода наименьших квадратов будет такая прамая 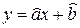 , для которой сумма S минимальна.
, для которой сумма S минимальна.
Если приравнять нулю производные 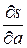 и
и 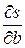 , то получим систему двух линейных по а и b уравнений, из которых в конечном счете можно найти решение:
, то получим систему двух линейных по а и b уравнений, из которых в конечном счете можно найти решение:
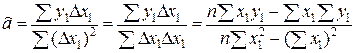 (26)
(26)
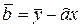 (27)
(27)
где 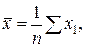 и
и 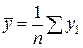 - среднее арифметическое, знак
- среднее арифметическое, знак 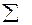 означает
означает 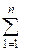 - суммирование по всем точкам.
- суммирование по всем точкам.
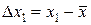 .
.
Как видим, для углового коэффициента 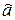 МНК - прямой в (26) даны три эквивалентных формулы.
МНК - прямой в (26) даны три эквивалентных формулы.
Подставив из (27) выражение для 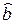 в формулу
в формулу 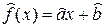 , получим уравнение МНК-прямой
, получим уравнение МНК-прямой
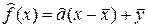 (28)
(28)
откуда видно, что 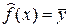 , т.е. эта прямая всегда проходит через точку (
, т.е. эта прямая всегда проходит через точку ( 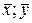 ), являющуюся центром тяжести данной системы точек.
), являющуюся центром тяжести данной системы точек.
Пример 32. Для данных в таблице 13 пяти точек найти МНК - прямую и сумму 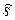 квадратов отклонений от нее.
квадратов отклонений от нее.
Таблица 13
Обработка данных для нахождения МНК-прямой
| N точки | x1 | y1 | Δx1 | y1Δx1 | (Δx1)2 | f(x1) | 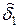
| 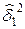
|
| 2,5 | -1,8 | -4,4 | 3,24 | 2,45 | 0,05 | 0,0025 | ||
| 2,2 | -0,8 | -1,76 | 0,64 | 2,0 | 0,2 | 0,04 | ||
| 1,2 | 1,2 | 1,44 | 1,1 | -0,1 | 0,01 | |||
| 0,7 | 2,2 | 1,54 | 4,84. | 0,65 | 0,05 | 0,0025 | ||
| 1,8 | 1,8 | -1,44 | 0,64 | 2,0 | -0,2 | 0.04 | ||
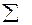
| 8, 2 | -4,86 | 10,8 | - | 0,095 |
n=5; 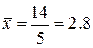 ;
; 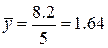 ;
;
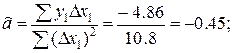
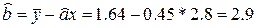
МНК – прямая 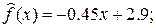
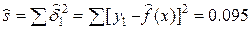
Для контроля полезны суммы : 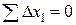 и
и 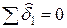 .
.
Метод наименьших квадратов применим не только к прямой, но и к широкому классу функций не только на плоскости, но и в пространстве. Как и во всей статистике, здесь важна интерпретация (истолкование) полученных результатов. Это возможно лишь в рамках принятой вероятностной модели. Поэтому нужно описать принимаемую модель. Например, если мы принимаем, что обрабатываемые точки для системы двух нормальных сл.величин {X, Y) (т.e. [x1; y1 ) - реализации двумерной нормальной сл.величины (X;Y)), то полученная МНК - прямая будет оценкой регрессии Y на Х, а ее угловой коэффициент 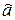 выражается через отношение стандартных отклонений и выборочный коэффициент корреляции
выражается через отношение стандартных отклонений и выборочный коэффициент корреляции 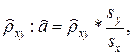 где sx2 и sy2 - выборочные дисперсии для X и Y.
где sx2 и sy2 - выборочные дисперсии для X и Y.
Дата добавления: 2016-02-27; просмотров: 2549;
