ОБЩАЯ СХЕМА ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ

1. Строим критерий с известным распределением.

2. По заданному уровню значимости строим границы критической области .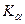

3. Строим по выборке опытное значение критерия .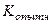

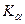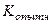4. Сравниваем значения и , если 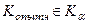, то делаем вывод о том, что опытные данные противоречат выдвинутой гипотезе и отвергаем ее.

ПРИМЕРЫ

Рассмотрим сначала задачи проверки гипотез об интересующем нас параметре θ вида:

1) H₀: θ=θ₀; H₁: θ 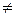θ₀,

2) H₀: θ=θ₀; H₁: θ<θ₀,

3) H₀: θ=θ₀; H₁: θ>θ₀.

где θ₀ - заданное конкретное число.

Такие гипотезы можно проверить посредствен построения доверительного интервала для θ.

Для проверки гипотезы вида 1) мы строим с доверительной вероятностью β=1-α доверительный двусторонний интервал I_β (θ) для θ и проверяем, накрыл ли он число θ_0.

Если θ₀ Є I_β(θ), то гипотеза Ho выдержала проверку, т.е. приемлема с уровнен значимости α. Если θ₀ 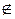I_β(θ), т.е. интервал не накрыл θ₀, то гипотезу Н₀ отбрасываем, принимая Н₁.

При проверке гипотез вида 2) и 3) строится односторонний доверительный интервал, а именно, в случае 2) односторонний интервал I_β(θ) с нижней границей х_H; а в случае 3) с верхней границей х_B . Если этот интервал покрывает θ₀, гипотеза Н₀ принимается, если не накрывает - отвергается.

Пример 29.

Допустим, при уровне значимости α=0,05, проверяется гипотеза Но: μ=109 против альтернативной, Н₁: μ 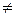109 для генерального среднего μ сл.величины X~N(μ, σ² }. X - длина детали, μ=MХ. По техническим требованиям среднее μ должно равняться номинальному размеру μо=109, что и проверяется на основе выборки из n=31 детали. Их размеры мы здесь не приводим, а сразу даем подсчитанное выборочное среднее 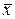=100 и выборочную дисперсию s²=20². Находим доверительную вероятность β=1-α=1-0,05=0,95 и ν=n-1=30.

Далее .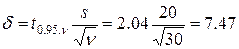

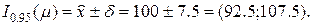
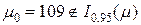=>гипотеза Н₀ отклоняется. Вывод: генеральное среднее не равно по минимальному значению.

Пример 30.

При уровне значимости α=0,05 проверить гипотезу Н₀: μ=106, H₁: μ>106 по выборке предыдущего примера. Чтобы построить 95%-ый односторонний доверительный интервал для среднего, сначала строим 90%-ный двусторонний. 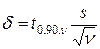. Но коэффициента t_0.90.ν; нет в таблице 10. Зато в таблице 7 есть для сл.величины t₃₀ квантиль уровня 0,95, равный 1,70. Значит, левее точки 1,70 лежит 0,95% площади распределения. А так как кривая t.-распределения симметричная, то 5% площади лежит не только правее точки 1,70, но и левее точки -1,70, а между -1,70 и +1,70 лежит 90% площади. Но t_0.90.ν как раз обозначает такое число, что в интервале (-t_0.90.ν; +t_0.90.ν) заключено 90% площади, а остальная площадь поровну лежит слева и справа. Поэтому t_0.90.30=1.70.

В результате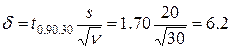

Двухсторонний доверительный 90%-й интервал найден: I_0.90(μ)=100±6,2=(93,8; 106,2).

Опустив нижнюю границу интервала до - 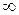, мы увеличиваем доверительную вероятность β на величину 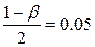и приходим к β=0.95.

Итак, получен 95% -й односторонний доверительный интервал для математического ожидания μ с верхней границей 106,2: I_0.95(μ)=(- 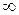; 106,2).

Число μо=106 принадлежит этому интервалу, поэтому приемлема гипотеза Н₀ о том, что математическое ожидание μ (оно жe истинное среднее μ, генеральное среднее) равно 106.

Подчеркнем, что вывод о приемлемости основной гипотезы Н₀, ее не противоречивости имеющимся данным не означают того, что доказана ее истинность. Так категорично утверждать нельзя. В последнем примере не противоречили бы тем же опытным данным гипотезы Н₀: μ=100, или Н₀: μ=105 и вообще бесконечное число промежуточных гипотез, из которых больше одной верной быть не может.

Не исключено, что основная гипотеза Н₀ могла не противоречить данным только из-за их недостатка, а будь числo наблюдений больше в два-три раза, это противоречие наблюдениям выявилось бы.