ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ДИСПЕРСИИ

Формула доверительного интервала для дисперсии DX зависит от вида закона распределения cл. величины X. Мы рассмотрим нормальный закон: X~N(μ, σ ² ). Если величина X в первом испытании обозначена X₁ , во втором - X₂, … в п-ном X_n, то в случайной выборке X₁, X₂, …,X_n все величины независимы и распределены по закону N(μ, σ²). Нормируя величину X₁~ N(μ, б²), получим

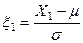~N(0,1), т.к. ,

.

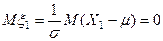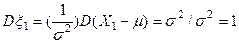Поэтому ел. величина 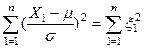- сумма квадратов n независимых стандартных нормальных величин. Такая сумма обозначается, как помним, 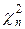и читается: хи-квадрат с n степенями свободы.

Таким образом, 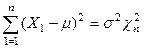и

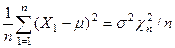
Поскольку величина 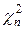/n близка 1 (а среднее ее как раз 1), то в случае, если истинное среднее μ нам известно, за оценку дисперсии σ²=DХ лучше всего взять величину

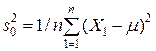(18)

Эта величина 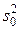распределена как сл, величина 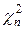, умноженная на число σ²/n.

Однако реально истинное μ чаще неизвестно. В этом случае вместо μ в формулу входит 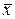и доказывается, что

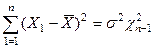(19)

Вспоминая, что левую сумму в (19) раньше обозначали 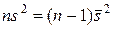, запишем

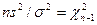(20).

Равенство (20) позволяет построить доверительный интервал для дисперсии DХ=σ² нормального закона для заданной гарантии β. Обозначим α=1–β, 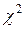- квантиль уровня α/2 распределения 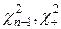- квантиль уровня 1–α/2 того же распределения (рис.10).

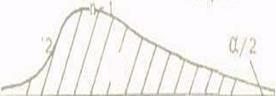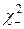Точки - и 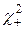выбраны так, что 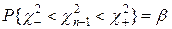, это равенство с учетом (20) перепишем в виде 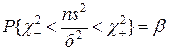(21)

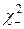рис.10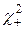

Остается произвести преобразование неравенства, стоящего в скобках. Нетрудно проверить, что оно эквивалентно такому:

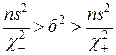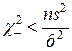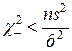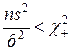. (Действительно, , эквивалентно , а , эквивалентно ).

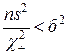Заменяя в (21) неравенство на эквивалентное, окончательно получим:

.

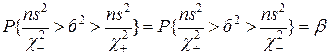Последнее означает, что числа 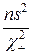и 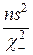являются границами доверительного интервала для дисперсии б² с гарантией β:

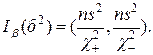(22).

Для σ доверительный интервал получим извлечением корня из границ предыдущего

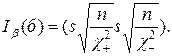
Заметим, наконец, что малая дисперсия DХ почти всегда выгодна, а большая невыгодна на практике. Поэтому имеет смысл искать односторонний доверительный интервал для дисперсии, для чего нижнюю его границу приравниваем нулю, а верхнюю находим из условия:

,

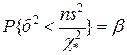где 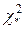- квантиль уровня (1-β) сл.величины .

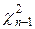Заканчивая тему оценивания, подчеркнем: математическая статистика рассматривает не всякие случайные эксперименты (значит, не всякие результаты n измерений x₁ ,х₂,. . . . ,х_n признает выборкой),а только такие, где есть статистическая устойчивость ,т. е. она предполагает одинаковость условий проведения эксперимента).