КРИТЕРИЙ КОЛМОГОРОВА-СМИРНОВА ДЛЯ ПРОВЕРКИ ПРОСТОЙ ГИПОТЕЗЫ
Имеется случайная величина X , имеется выборка объема n: x1, x2,...,xn. Выдвинута простая гипотеза о функции распределения F(x). По результатам статистический испытаний необходимо проверить простую гипотезу.
По выборке строится вариационный ряд x(1), x(2),..., x(n). Предполагается, что случайная величина X является непрерывной и, следовательно, члены выборки не совпадают.
Зададим эмпирическую функцию распределения случайной величины X, которая равна
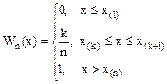
Эмпирическая функция распределения - это оценка теоретической функции распределения.
k - количество результатов испытания, которые левее x, n - общее количество результатов испытания.
Если проверяемая гипотеза верна, то на основании теоремы Гливенко при числе испытаний стремящихся к бесконечности по вероятности эмпирическая функция распределения равномерно сходится к теоретической.
Рассмотрим случайную величину w2.
Очевидно, что при n®¥ в случае истинности гипотезы w2®¥.
Доказано, что при n®¥ случайная величина nw2 имеет нормальное распределение. При этом при n³40 nw2 практически не отличается от предельного распределения (полученного эмпирическим путем). Очевидно, что в качестве критической области выбирается область больших положительных значений критерия.
Как мы уже раньше представляли выражение для w2.
т.к. мы разбили область интегрирования на интервалы из-за скачка.
Наконец, объединяя члены, зависящие от F(x(k)) (с заданным k=1, 2, ...n), находящиеся в двух суммах получаем 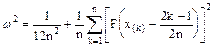
КРИТЕРИЙ «ИДЕАЛЬНОГО НАБЛЮДАТЕЛЯ» (ЗИГЕРТА-КОТЕЛЬНИКОВА)
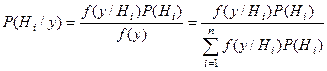 ,
, 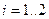
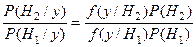
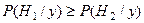
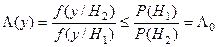
Дата добавления: 2016-02-27; просмотров: 773;
